Touring multivariate data

SISBID 2025
https://github.com/dicook/SISBID

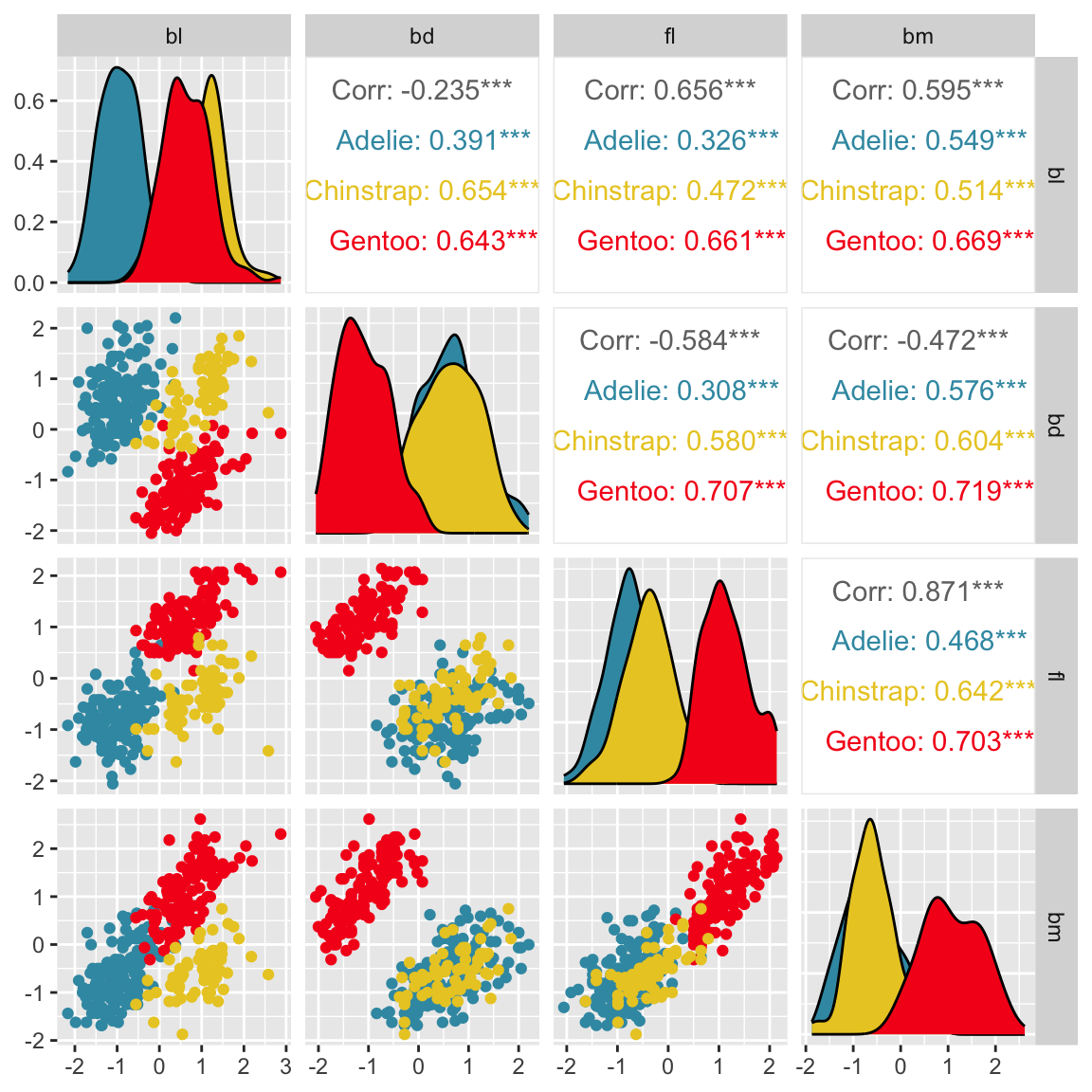
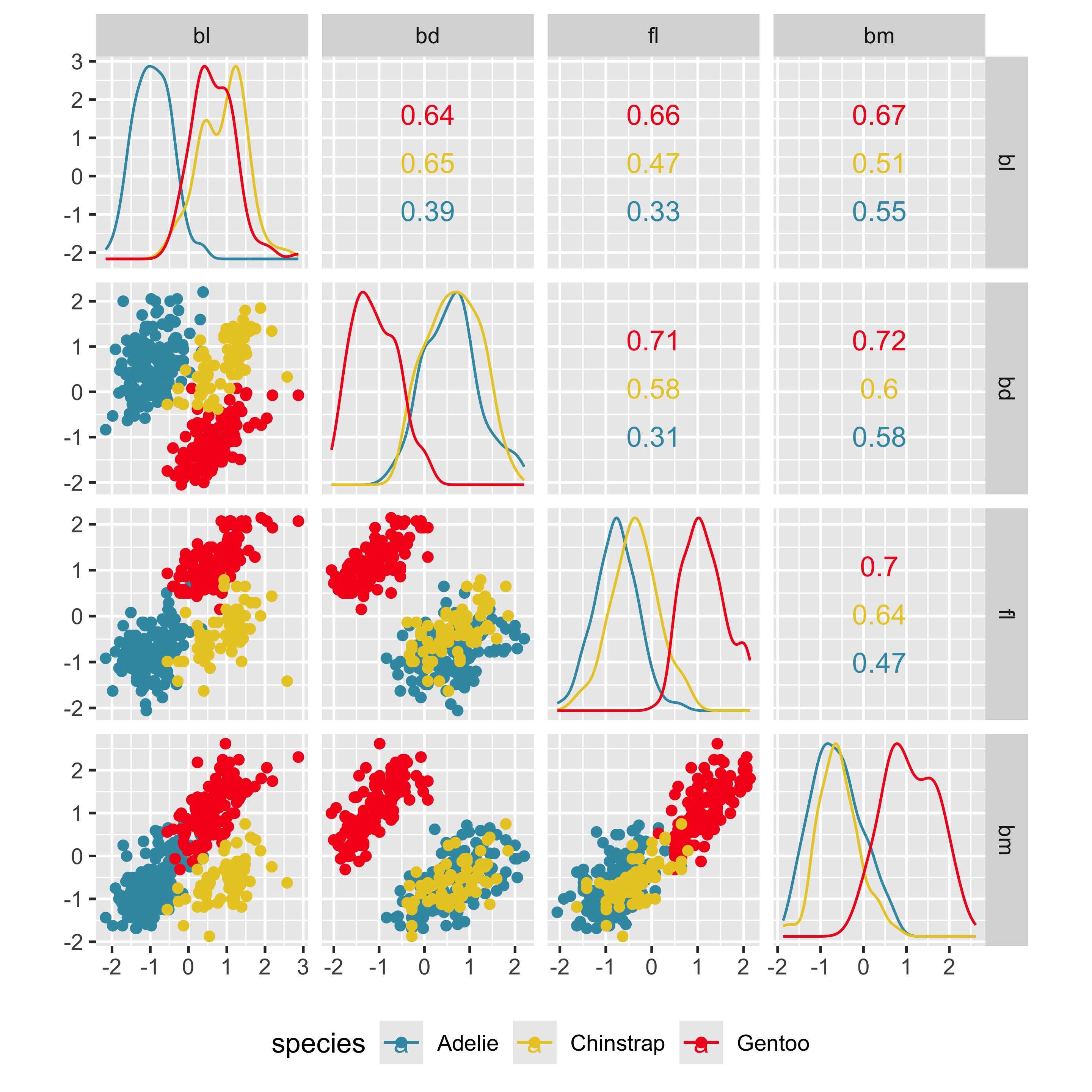
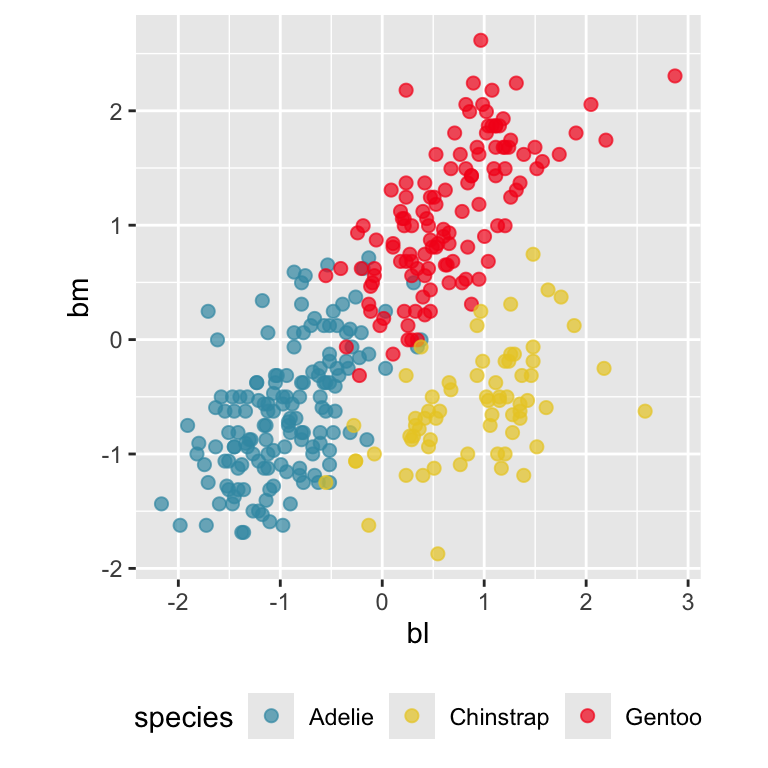
Pairwise plots

What don’t you see?



Unless you have tours, you’ll never know 🫣

Our first tour

What patterns do you see?

# Run the tour
animate_xy(penguins_std[,2:5], 
           col=penguins_std$species, 
           axes="off", 
           fps=10)

What new things do we learn?

  • The separation between clusters is larger and
  • there are a few more unusual penguins.

What did you see?

  • clusters ✅
  • outliers ✅
  • linear dependence ✅
  • elliptical clusters with slightly different shapes ✅
  • separated elliptical clusters with slightly different shapes ✅

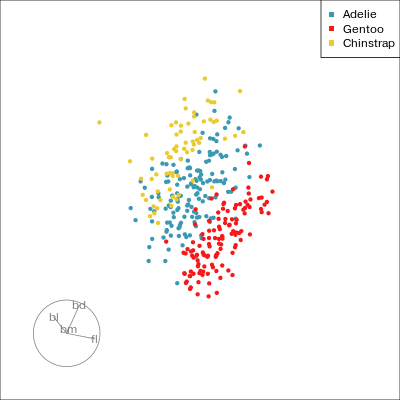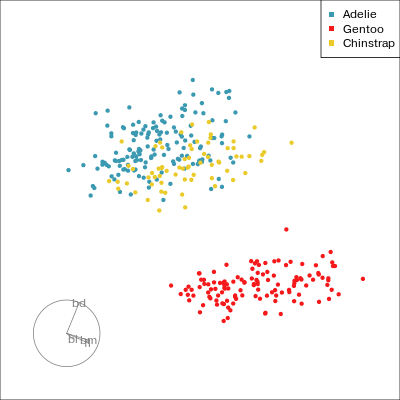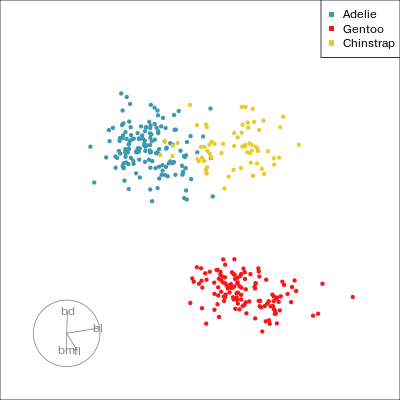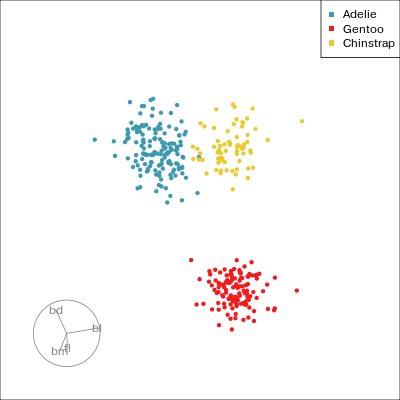
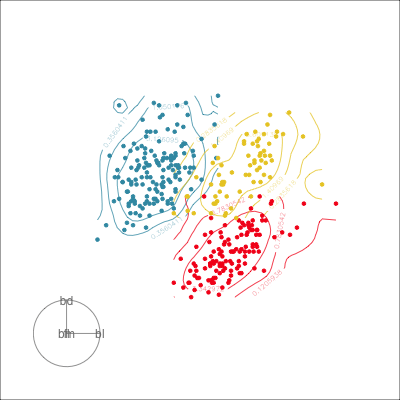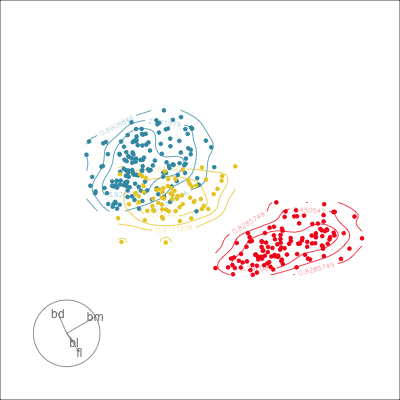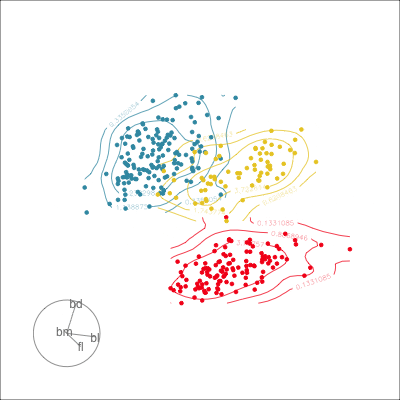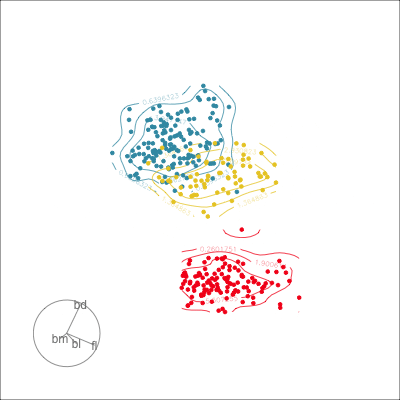
Which shows better separation?

What is a tour?

  • a movie of low-dim projections
  • constructed to come close to showing all possible low-dim projections
  • a grand tour is a space-filling curve in the manifold of low-dim projections of high-dim data spaces.

\({\mathbf x}_i \in \mathcal{R}^p\), \(i^{th}\) data vector

\(F\) is a \(p\times d\) orthonormal basis

\(F'F=I_d\), where \(d\) is the projection dimension.

The projection of \({\mathbf x_i}\) onto \(F\) is \({\mathbf y}_i=F'{\mathbf x}_i\).

Tour is indexed by time, \(F(t)\), where \(t\in [a, z]\). Starting and target frame denoted as \(F_a = F(a), F_z=F(t)\).

The animation of the projected data is given by a path \({\mathbf y}_i(t)=F'(t){\mathbf x}_i\).

Geodesic interpolation b/w planes

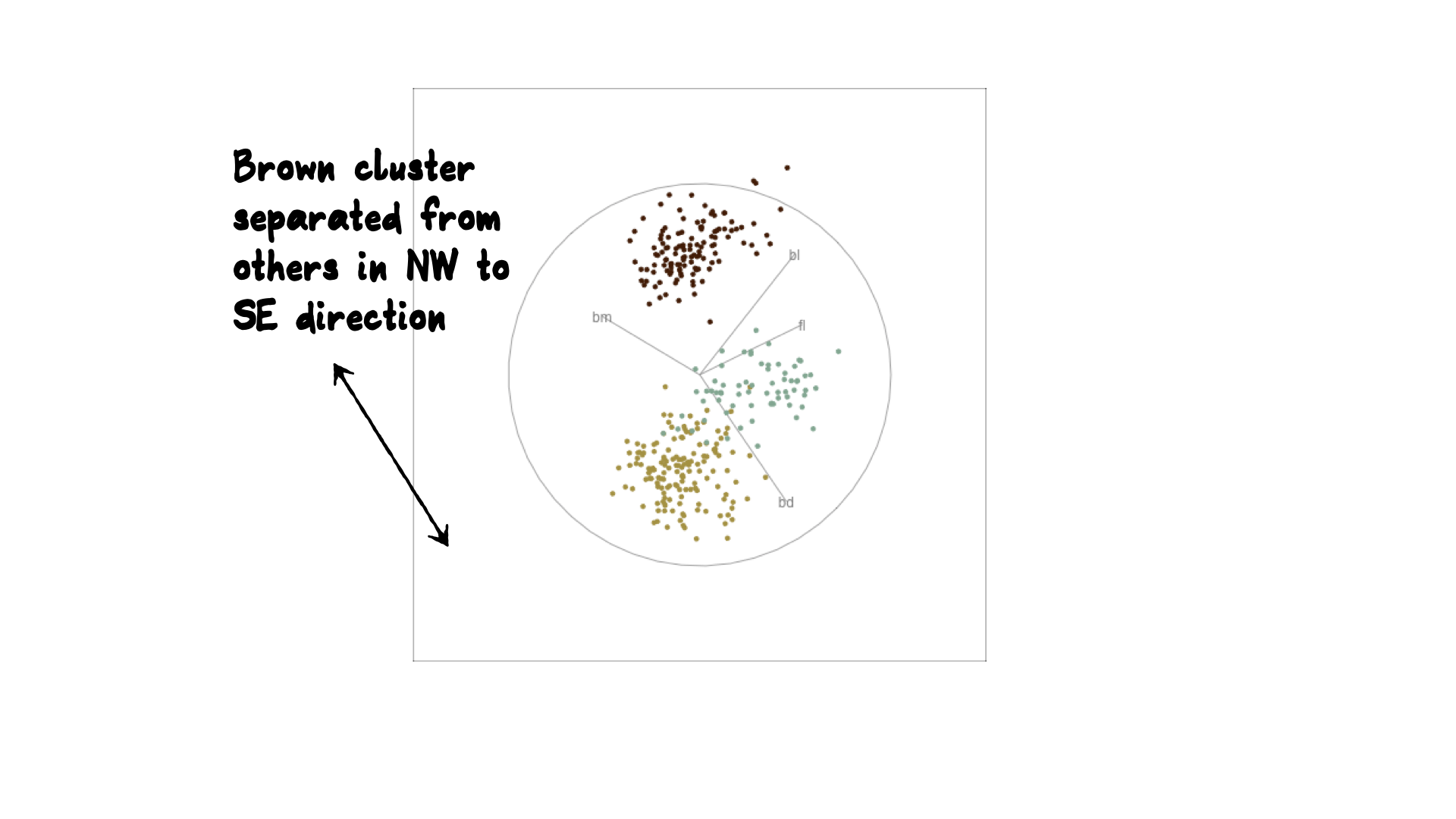
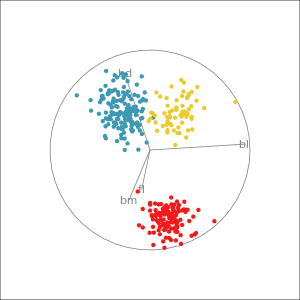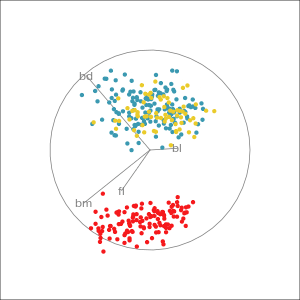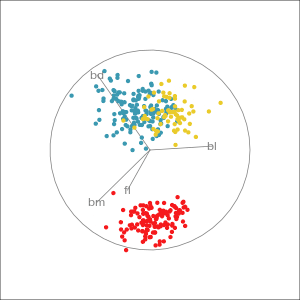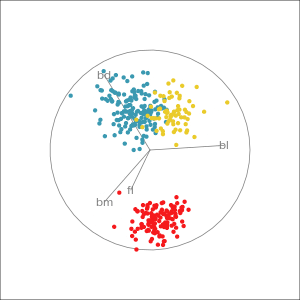
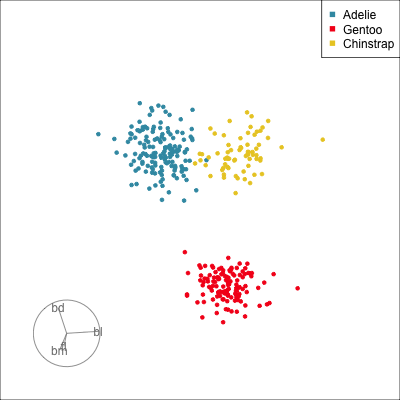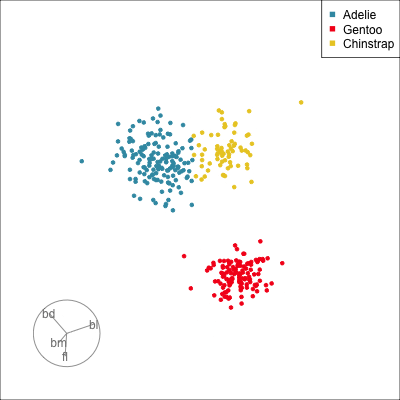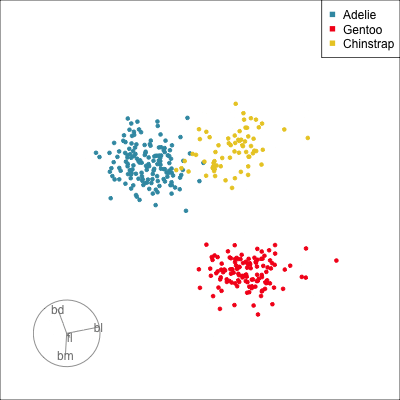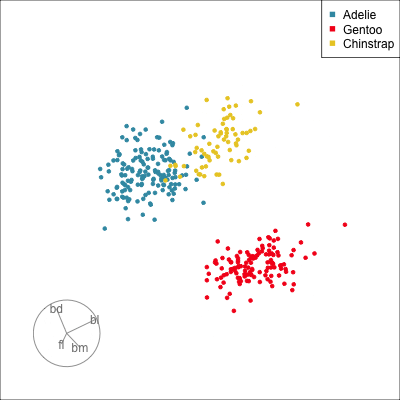
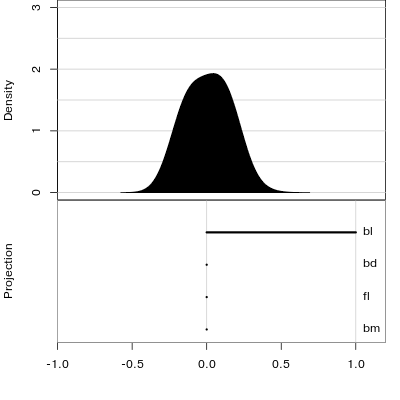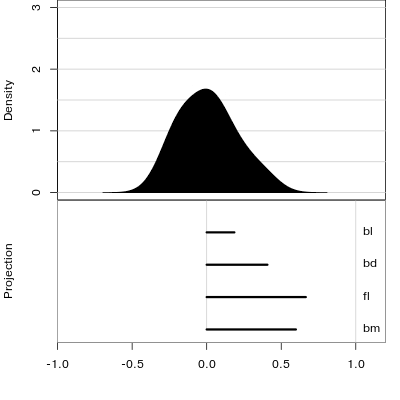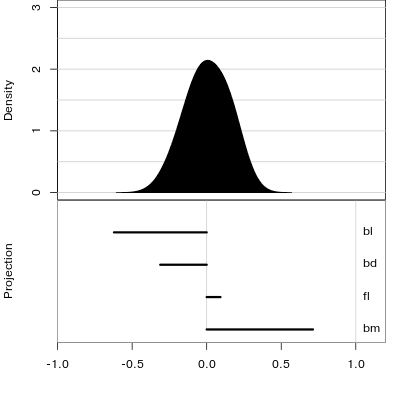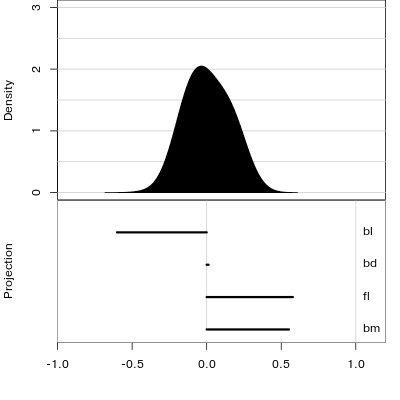
Tour is indexed by time, \(F(t)\), where \(t\in [a, z]\). Starting and target frame denoted as \(F_a = F(a), F_z=F(t)\).

The animation of the projected data is given by a path \({\mathbf y}_i(t)=F'(t){\mathbf x}_i\).

Reading axes - interpretation

Length and direction of axes relative to the pattern of interest

Reading axes - interpretation

Length and direction of axes relative to the pattern of interest

Understanding a tour

Understanding the projections

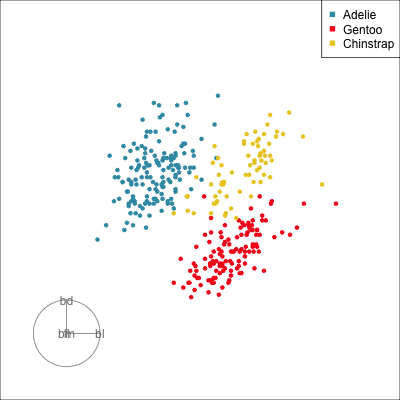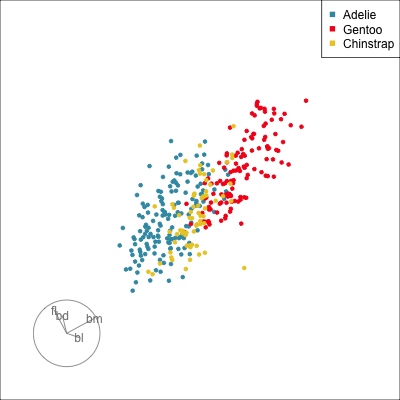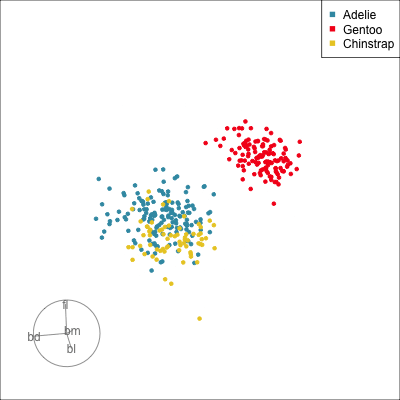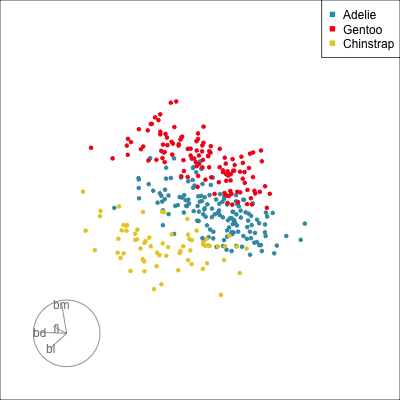
ggplot(penguins_std, 
   aes(x=fl, y=bd,
       colour=species)) +
  geom_point(alpha=0.7, size=2) +
  scale_colour_discrete_divergingx(palette = "Zissou 1") + 
  theme(aspect.ratio=1,
  legend.position="bottom")

Gentoo from others in contrast of fl, bd

ggplot(penguins_std, 
   aes(x=bl, y=bm,
       colour=species)) +
  geom_point(alpha=0.7, size=2) +
  scale_colour_discrete_divergingx(palette = "Zissou 1") + 
  theme(aspect.ratio=1,
  legend.position="bottom")

Chinstrap from others in contrast of bl, bm

Difficulties in making interpretations

  • There may be multiple and different combinations of variables that reveal similar structure. ☹️
  • This is due to association between variables in the multivariate data.
  • The tour can help to discover these, too. 😂

Other tour types

  • guided: follows the optimisation path for a projection pursuit index.
  • little: interpolates between all variables.
  • local: rocks back and forth from a given projection, so shows all possible projections within a radius.
  • dependence: two independent 1D tours
  • frozen: fixes some variable coefficients, others vary freely.
  • manual: control coefficient of one variable, to examine the sensitivity of structure this variable. (In the spinifex package)
  • slice: use a section instead of a projection.
  • sage: transform a 2D projection, to avoid data piling.

Guided tour

New target bases are chosen using a projection pursuit index function

\[\mathop{\text{maximize}}_{F}~g(xF) ~~~\text{ subject to } F \text{ being orthonormal}\]

  • holes: This is an inverse Gaussian filter, which is optimised when there is not much data in the center of the projection, i.e. a “hole” or donut shape in 2D.
  • central mass: The opposite of holes, high density in the centre of the projection, and often “outliers” on the edges.
  • LDA/PDA: An index based on the linear discriminant dimension reduction (and penalised), optimised by projections where the named classes are most separated.

Grand

Might accidentally see best separation

Guided, using LDA index

Moves to the best separation

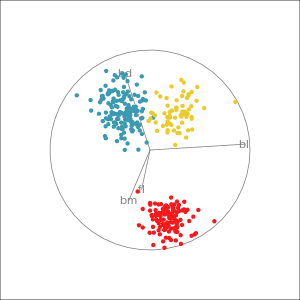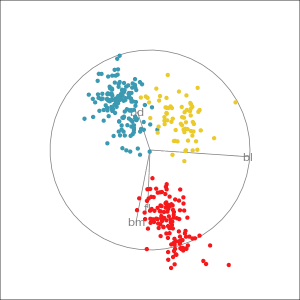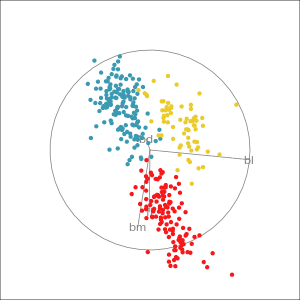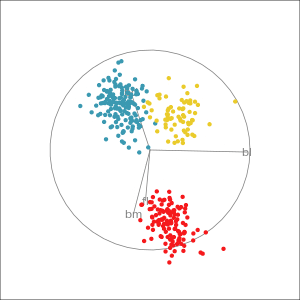
Manual tour

  • start from best projection, given by projection pursuit
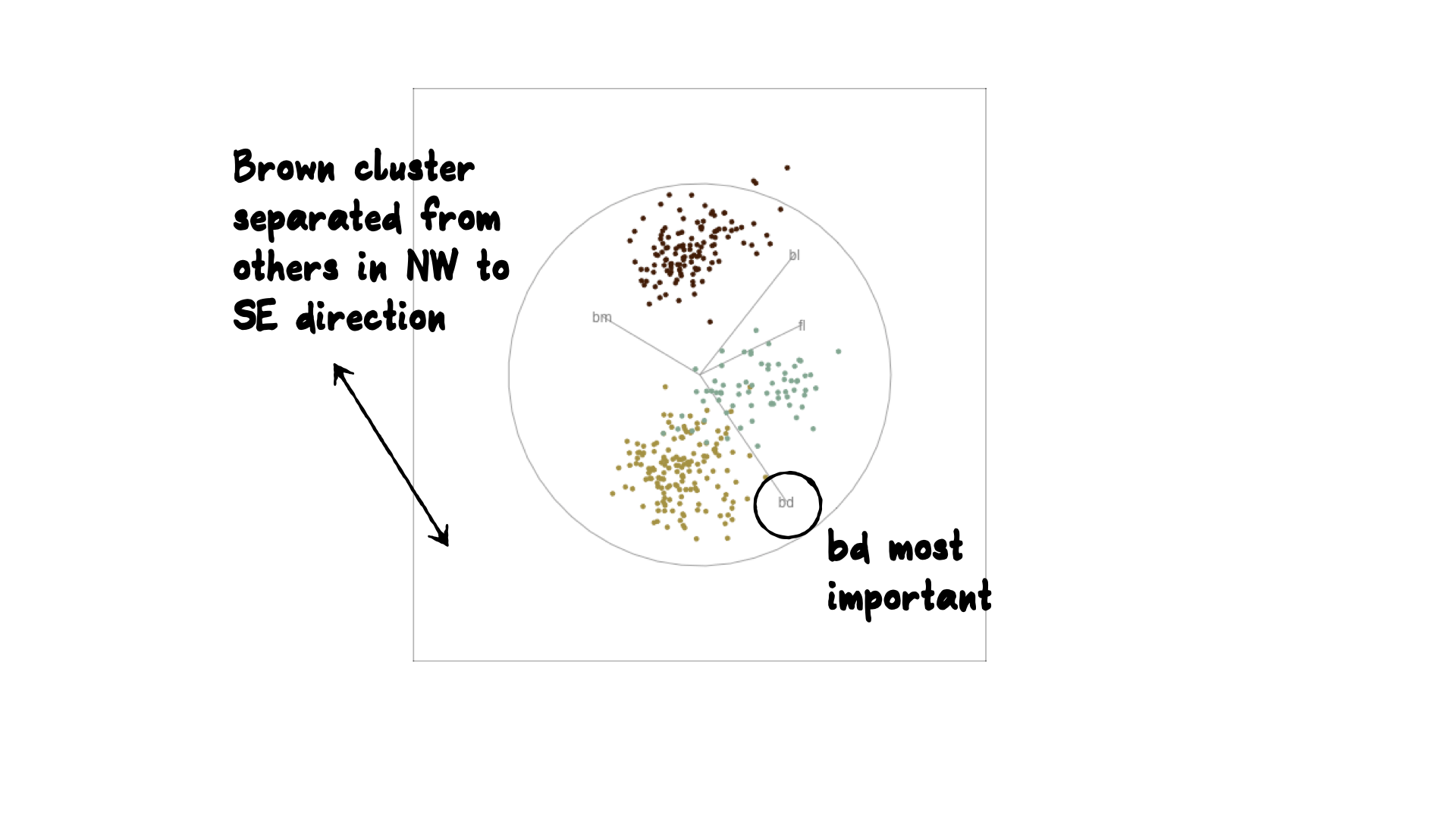
  • bd contribution controlled
  • if bd is removed from projection, Gentoo separation disappears
  • bd is important for distinguishing Gentoo
# Check contribution of bl, 
# change mvar to switch variables
animate_xy(penguins_std[,2:5], 
           radial_tour(as.matrix(best_proj), mvar = 2),
           col = penguins_std$species)

Manual tour

  • start from best projection, given by projection pursuit
  • bl contribution controlled
  • bl is important for distinguishing Adelie from Chinstrap

Local Tour

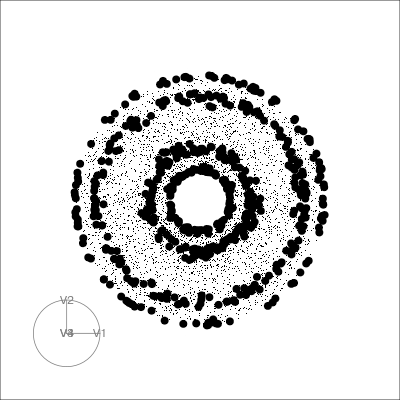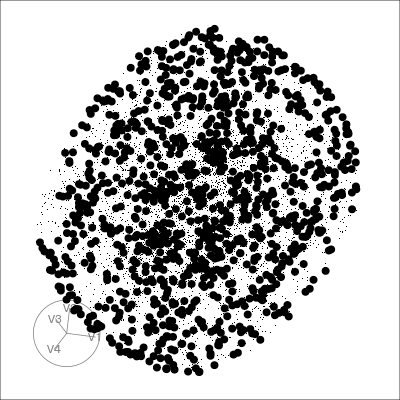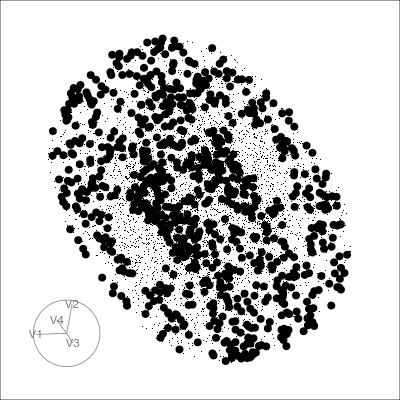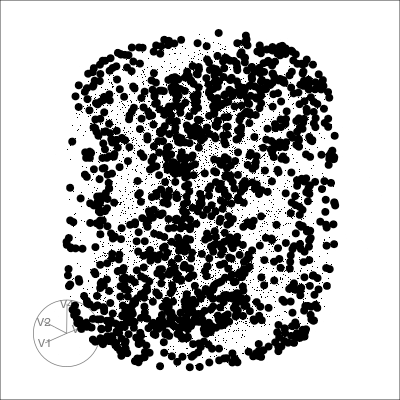
Rocks from and to a given projection, in order to observe the neighbourhood

Geometric shapes with slice tour

Solid 4D sphere

library(geozoo)
sphere2 <- sphere.solid.random(p=4)$points %>% as_tibble()
animate_slice(sphere2, axes="bottomleft")

Hollow 4D sphere

sphere1 <- sphere.hollow(p=4)$points %>% as_tibble()
animate_slice(sphere1, axes="bottomleft", half_range=0.6)

Geometric shapes with slice tour

4D Torus

torus <- torus(p = 4, n = 5000, radius=c(8, 4, 1))$points %>% as_tibble()
animate_slice(torus, axes="bottomleft", half_range=0.8)

4D Hollow Cube

cube1 <- cube.face(p=4)$points %>% as_tibble()
# Slicing needs data to be on a standard scale
cube1_std <- cube1 %>% 
  mutate(across(where(is.numeric),  ~ scale(.)[,1]))
animate_slice(cube1_std, axes="bottomleft")

PCA tour

Compute PCA, reduce dimension, show original variable axes in the reduced space.

penguins_pca <- prcomp(penguins_std[,2:5], 
                       center = FALSE)
penguins_coefs <- penguins_pca$rotation[, 1:3]
penguins_scores <- penguins_pca$x[, 1:3]

animate_pca(penguins_scores, pc_coefs = penguins_coefs, col=penguins_std$species)
render_gif(
  penguins_scores, grand_tour(), 
  display_pca(pc_coefs = penguins_coefs, 
              col=penguins_std$species,
              axes="bottomleft"), 
  "slides/images/penguins2d_pca.gif", 
  frames=100, width=400, height=400)

Projection dimension and displays

1D projections displayed as a density

animate_dist_cl(penguins_std[,2:5], 
                half_range=1.3)

Density contours overlaid on a scatterplot

animate_density2d(
  penguins_std[,2:5], 
  col=penguins_std$species, axes="bottomleft")

Your turn

Using the sample code from the tour package, check how many clusters are in the example data.

library(tourr)
data(flea)
?animate_xy
# On a Mac, start quartz window with:  quartz()
# On windows, start X11 window with:   X11()

animate_xy(flea[, 1:6])
# RStudio graphics windows: may want to reduce frame rate
animate_xy(flea[, 1:6], fps=10)

# Also
animate_xy(flea[, -7], col = flea$species)
animate_xy(flea[, 1:6], tour_path = guided_tour(lda_pp(flea$species)), col=flea$species)

Saving and sharing: Animated gif

render_gif(    
  penguins_std[,2:5], 
  grand_tour(), 
  display_xy(
    col=penguins_std$species, 
    axes="bottomleft"), 
  gif_file="slides/images/penguins2d.gif", 
  frames=100, 
  width=400, 
  height=400
)

Saving and sharing: single frame

Draw it with ggplot, and possibly pass to plotly.

load(here::here("data/p_tour_path.rda"))
penguins_pcti <- interpolate(
  penguins_pct, 0.2)
f27 <- matrix(
  penguins_pcti[,,27], 
  ncol=2)
p27 <- render_proj(
  penguins_std[,2:5],
  f27,
  obs_labels=
    penguins_std$species)

Resources

Creative Commons License This work is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.