8  Hierarchical clustering

8.1 Overview

Hierarchical cluster algorithms sequentially fuse neighboring points to form ever-larger clusters, starting from a full interpoint distance matrix. Distance between clusters is described by a “linkage method”, of which there are many. For example, single linkage measures the distance between clusters by the smallest interpoint distance between the members of the two clusters, complete linkage uses the maximum interpoint distance, and average linkage uses the average of the interpoint distances. Wards linkage, which usually produces the best clustering solutions, defines the distance as the reduction in the within-group variance. A good discussion on cluster analysis and linkage can be found in Boehmke & Greenwell (2019), on Wikipedia or any multivariate textbook.

Hierarchical clustering is summarised by a dendrogram, which sequentially shows points being joined to form a cluster, with the corresponding distances. Breaking the data into clusters is done by cutting the dendrogram at the long edges.

Here we will take a look at hierarchical clustering, using Wards linkage, on the simple_clusters data. The steps taken are to:

  1. Plot the data to check for presence of clusters and their shape.
  2. Compute the hierarchical clustering.
  3. Plot the dendrogram to help decide on an appropriate number of clusters, using the dendro_data function from the ggdendro package.
  4. Show the dendrogram overlaid on the data, calculated by the hierfly function in mulgar.
  5. Plot the clustering result, by colouring points in the plot of the data.

Load libraries 
data(simple_clusters)

# Compute hierarchical clustering with Ward's linkage
cl_hw <- hclust(dist(simple_clusters[,1:2]),
                method="ward.D2")
cl_ggd <- dendro_data(cl_hw, type = "triangle")

# Compute dendrogram in the data
cl_hfly <- hierfly(simple_clusters, cl_hw, scale=FALSE)

# Show result
simple_clusters <- simple_clusters %>%
  mutate(clw = factor(cutree(cl_hw, 2)))

Figure 8.1 illustrates the hierarchical clustering approach for a simple simulated data set (a) with two well-separated clusters in 2D. The dendrogram (b) is a representation of the order that points are joined into clusters. The dendrogram strongly indicates two clusters because the two branches representing the last join are much longer than all of the other branches.

Although, the dendrogram is usually a good summary of the steps taken by the algorithm, it can be misleading. The dendrogram might indicate a clear clustering (big differences in heights of branches) but the result may be awful. You need to check this by examining the result on the data, called model-in-the-data space by Wickham et al. (2015).

Plot (c) shows the dendrogram in 2D, overlaid on the data. The segments show how the points are joined to make clusters. In order to represent the dendrogram this way, new points (represented by a “+” here) need to be added corresponding to the centroid of groups of points that have been joined. These are used to draw the segments between other points and other clusters. We can see that the longest (two) edges stretches across the gap between the two clusters. This corresponds to the top of the dendrogram, the two long branches where we would cut it to make the two-cluster solution. This two-cluster solution is shown in plot (d).

Code to make the four plots
# Plot the data
pd <- ggplot(simple_clusters, aes(x=x1, y=x2)) +
  geom_point(colour="#3B99B1", size=2, alpha=0.8) +
  ggtitle("(a)") + 
  theme_minimal() +
  theme(aspect.ratio=1) 

# Plot the dendrogram
ph <- ggplot() +
  geom_segment(data=cl_ggd$segments, 
               aes(x = x, y = y, 
                   xend = xend, yend = yend)) + 
  geom_point(data=cl_ggd$labels, aes(x=x, y=y),
             colour="#3B99B1", alpha=0.8) +
  ggtitle("(b)") + 
  theme_minimal() +
  theme_dendro()

# Plot the dendrogram on the data
pdh <- ggplot() +
  geom_segment(data=cl_hfly$segments, 
                aes(x=x, xend=xend,
                    y=y, yend=yend)) +
  geom_point(data=cl_hfly$data, 
             aes(x=x1, y=x2,
                 shape=factor(node),
                 colour=factor(node),
                 size=1-node), alpha=0.8) +
  xlab("x1") + ylab("x2") +
  scale_shape_manual(values = c(16, 3)) +
  scale_colour_manual(values = c("#3B99B1", "black")) +
  scale_size(limits=c(0,17)) +
  ggtitle("(c)") + 
  theme_minimal() +
  theme(aspect.ratio=1, legend.position="none")

# Plot the resulting clusters
pc <- ggplot(simple_clusters) +
  geom_point(aes(x=x1, y=x2, colour=clw), 
             size=2, alpha=0.8) +
  scale_colour_discrete_divergingx(palette = "Zissou 1",
                                   nmax=5, rev=TRUE) +
  ggtitle("(d)") + 
  theme_minimal() +
  theme(aspect.ratio=1, legend.position="none")

pd + ph + pdh + pc + plot_layout(ncol=2)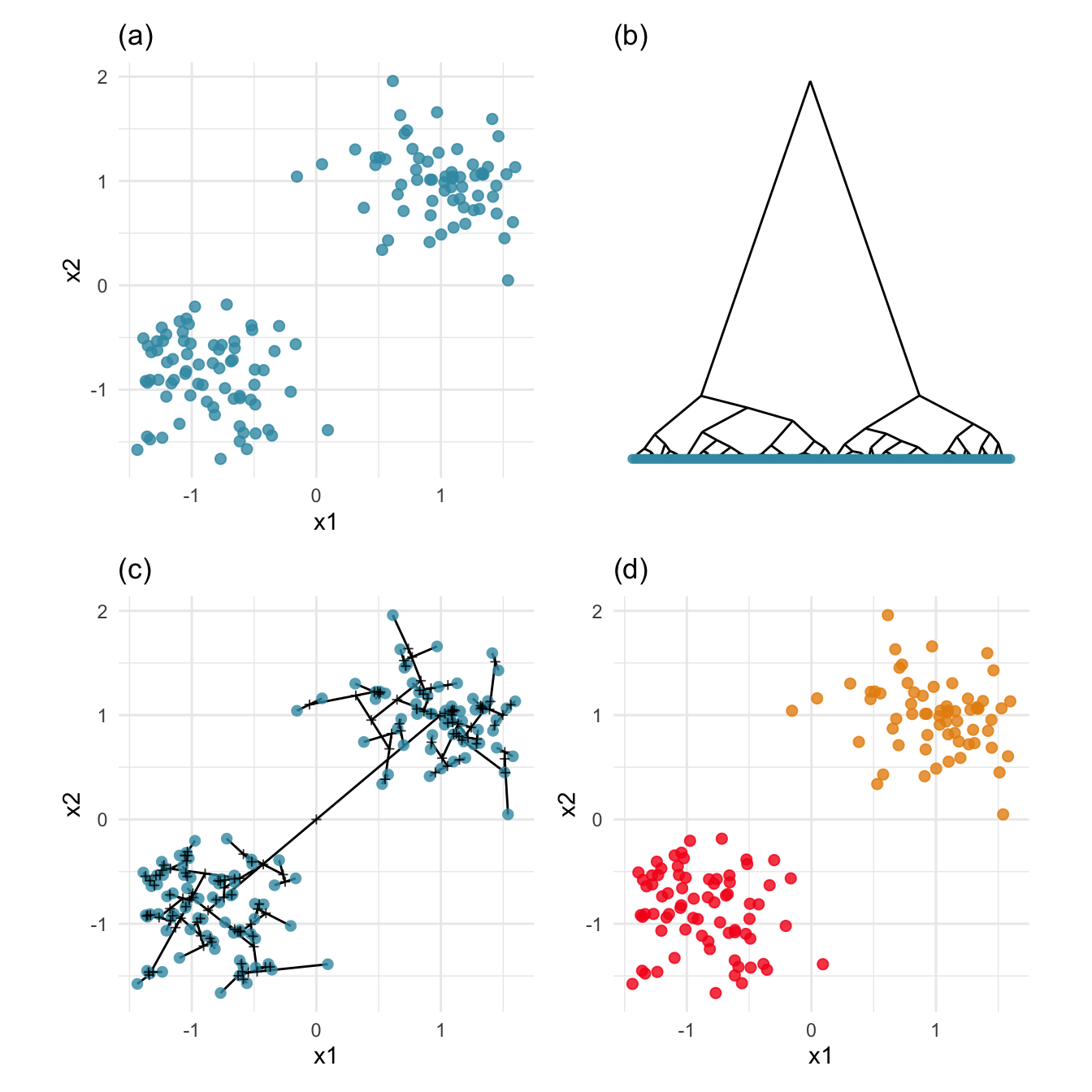
Figure 8.1: Hierarchical clustering on simulated data: (a) data, (b) dendrogram, (c) dendrogram on the data, and (d) two cluster solution. The extra points corresponding to nodes of the dendrogram are indicated by + in (c). The last join in the dendrogram (b), can be seen to correspond to the edges connecting the gap, when displayed with the data (c). The other joins can be seen to be pulling together points within each clump.

Plotting the dendrogram in the data space can help you understand how the hierarchical clustering has collected the points together into clusters. You can learn if the algorithm has been confused by nuisance patterns in the data, and how different choices of linkage method affects the result.

8.2 Common patterns which confuse clustering algorithms

Figure 8.2 shows two examples of structure in data that will confuse hierarchical clustering: nuisance variables and nuisance cases. We usually do not know that these problems exist prior to clustering the data. Discovering these iteratively as you conduct a clustering analysis is important for generating useful results.

Code to make plots
# Nuisance observations
set.seed(20190514)
x <- (runif(20)-0.5)*4
y <- x
d1 <- data.frame(x1 = c(rnorm(50, -3), 
                            rnorm(50, 3), x),
                 x2 = c(rnorm(50, -3), 
                            rnorm(50, 3), y),
                 cl = factor(c(rep("A", 50), 
                             rep("B", 70))))
d1 <- d1 %>% 
  mutate_if(is.numeric, function(x) (x-mean(x))/sd(x))
pd1 <- ggplot(data=d1, aes(x=x1, y=x2)) + 
  geom_point() +
    ggtitle("Nuisance observations") + 
  theme_minimal() +
    theme(aspect.ratio=1) 

# Nuisance variables
set.seed(20190512)
d2 <- data.frame(x1=c(rnorm(50, -4), 
                            rnorm(50, 4)),
                 x2=c(rnorm(100)),
                 cl = factor(c(rep("A", 50), 
                             rep("B", 50))))
d2 <- d2 %>% 
  mutate_if(is.numeric, function(x) (x-mean(x))/sd(x))
pd2 <- ggplot(data=d2, aes(x=x1, y=x2)) + 
  geom_point() +
    ggtitle("Nuisance variables") + 
  theme_minimal() +
    theme(aspect.ratio=1)

pd1 + pd2 + plot_layout(ncol=2)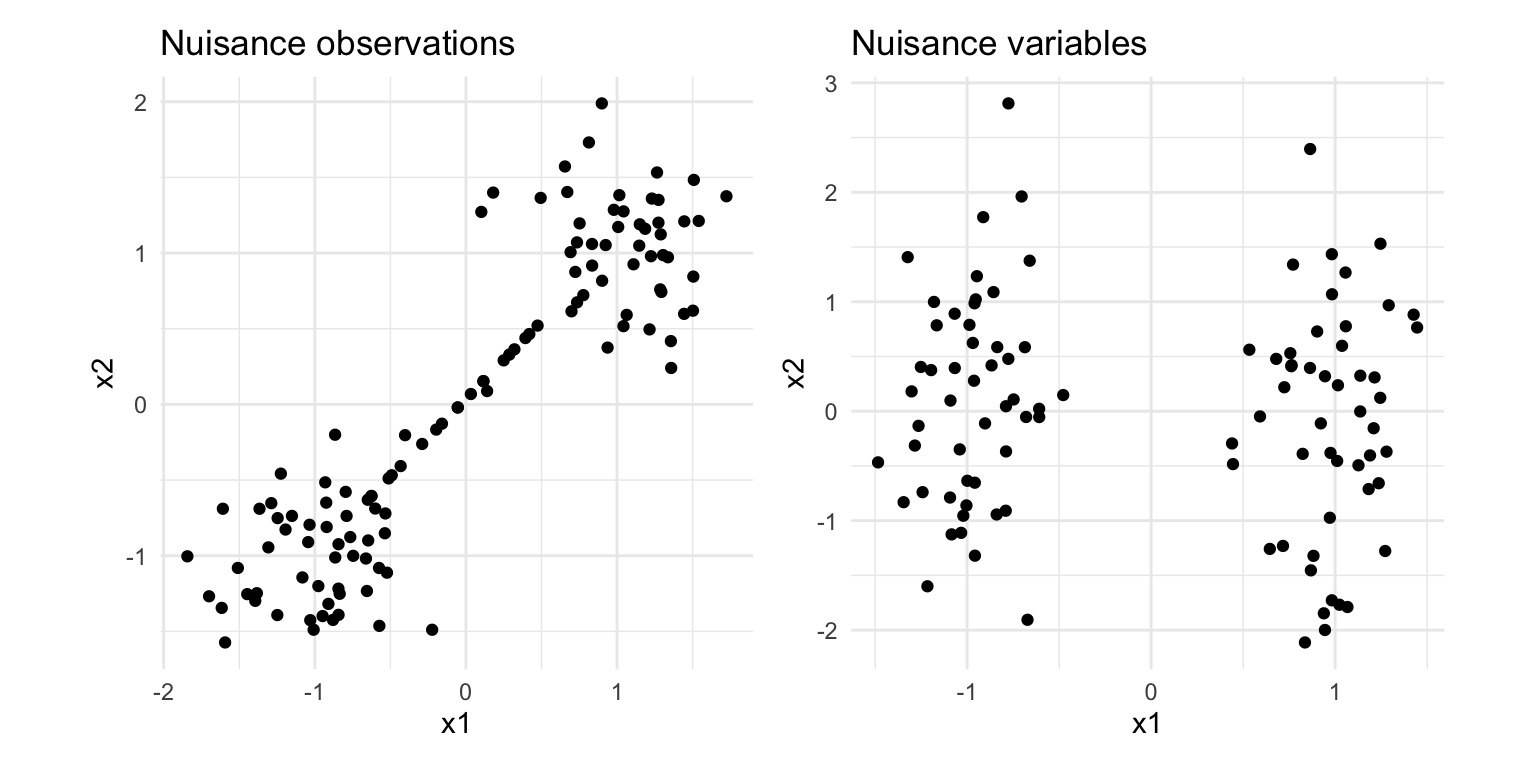
Figure 8.2: Two examples of data structure that causes problems for hierarchical clustering. Nuisance observations can cause problems because the close observations between the two clusters can cause some chaining in the hierarchical joining of observations. Nuisance variables can cause problems because observations across the gap can seem closer than observations at the end of each cluster.

If an outlier is a point that is extreme relative to other observations, an “inlier” is a point that is extreme relative to a cluster, but inside the domain of all of the observations. Nuisance observations are inliers, cases that occur between larger groups of points. If they were excluded there might be a gap between clusters. These can cause problems for clustering when distances between clusters are measured, and can be very problematic when single linkage hierarchical clustering is used. Figure 8.3 shows how nuisance observations affect single linkage but not Wards linkage hierarchical clustering.

Code to make plots
# Compute single linkage
d1_hs <- hclust(dist(d1[,1:2]),
                method="single")
d1_ggds <- dendro_data(d1_hs, type = "triangle")
pd1s <- ggplot() +
  geom_segment(data=d1_ggds$segments, 
               aes(x = x, y = y, 
                   xend = xend, yend = yend)) + 
  geom_point(data=d1_ggds$labels, aes(x=x, y=y),
             colour="#3B99B1", alpha=0.8) +
  theme_minimal() +
  ggtitle("(a) Single linkage dendrogram") +
  theme_dendro()

# Compute dendrogram in data
d1_hflys <- hierfly(d1, d1_hs, scale=FALSE)

pd1hs <- ggplot() +
  geom_segment(data=d1_hflys$segments, 
                aes(x=x, xend=xend,
                    y=y, yend=yend)) +
  geom_point(data=d1_hflys$data, 
             aes(x=x1, y=x2,
                 shape=factor(node),
                 colour=factor(node),
                 size=1-node), alpha=0.8) +
  scale_shape_manual(values = c(16, 3)) +
  scale_colour_manual(values = c("#3B99B1", "black")) +
  scale_size(limits=c(0,17)) +
  ggtitle("(b) Dendrogram in data space") + 
  theme_minimal() +
  theme(aspect.ratio=1, legend.position="none")

# Show result
d1 <- d1 %>%
  mutate(cls = factor(cutree(d1_hs, 2)))
pc_d1s <- ggplot(d1) +
  geom_point(aes(x=x1, y=x2, colour=cls), 
             size=2, alpha=0.8) +
  scale_colour_discrete_divergingx(palette = "Zissou 1",
                                   nmax=4, rev=TRUE) +
  ggtitle("(c) Two-cluster solution") + 
  theme_minimal() +
  theme(aspect.ratio=1, legend.position="none")

# Compute Wards linkage
d1_hw <- hclust(dist(d1[,1:2]),
                method="ward.D2")
d1_ggdw <- dendro_data(d1_hw, type = "triangle")
pd1w <- ggplot() +
  geom_segment(data=d1_ggdw$segments, 
               aes(x = x, y = y, 
                   xend = xend, yend = yend)) + 
  geom_point(data=d1_ggdw$labels, aes(x=x, y=y),
             colour="#3B99B1", alpha=0.8) +
  ggtitle("(d) Ward's linkage dendrogram") +
  theme_minimal() +
  theme_dendro()

# Compute dendrogram in data
d1_hflyw <- hierfly(d1, d1_hw, scale=FALSE)

pd1hw <- ggplot() +
  geom_segment(data=d1_hflyw$segments, 
                aes(x=x, xend=xend,
                    y=y, yend=yend)) +
  geom_point(data=d1_hflyw$data, 
             aes(x=x1, y=x2,
                 shape=factor(node),
                 colour=factor(node),
                 size=1-node), alpha=0.8) +
  scale_shape_manual(values = c(16, 3)) +
  scale_colour_manual(values = c("#3B99B1", "black")) +
  scale_size(limits=c(0,17)) +
  ggtitle("(e) Dendrogram in data space") + 
  theme_minimal() +
  theme(aspect.ratio=1, legend.position="none")

# Show result
d1 <- d1 %>%
  mutate(clw = factor(cutree(d1_hw, 2)))
pc_d1w <- ggplot(d1) +
  geom_point(aes(x=x1, y=x2, colour=clw), 
             size=2, alpha=0.8) +
  scale_colour_discrete_divergingx(palette = "Zissou 1",
                                   nmax=4, rev=TRUE) +
  ggtitle("(f) Two-cluster solution") + 
  theme_minimal() +
  theme(aspect.ratio=1, legend.position="none")

pd1s + pd1hs + pc_d1s + 
  pd1w + pd1hw + pc_d1w +
  plot_layout(ncol=3)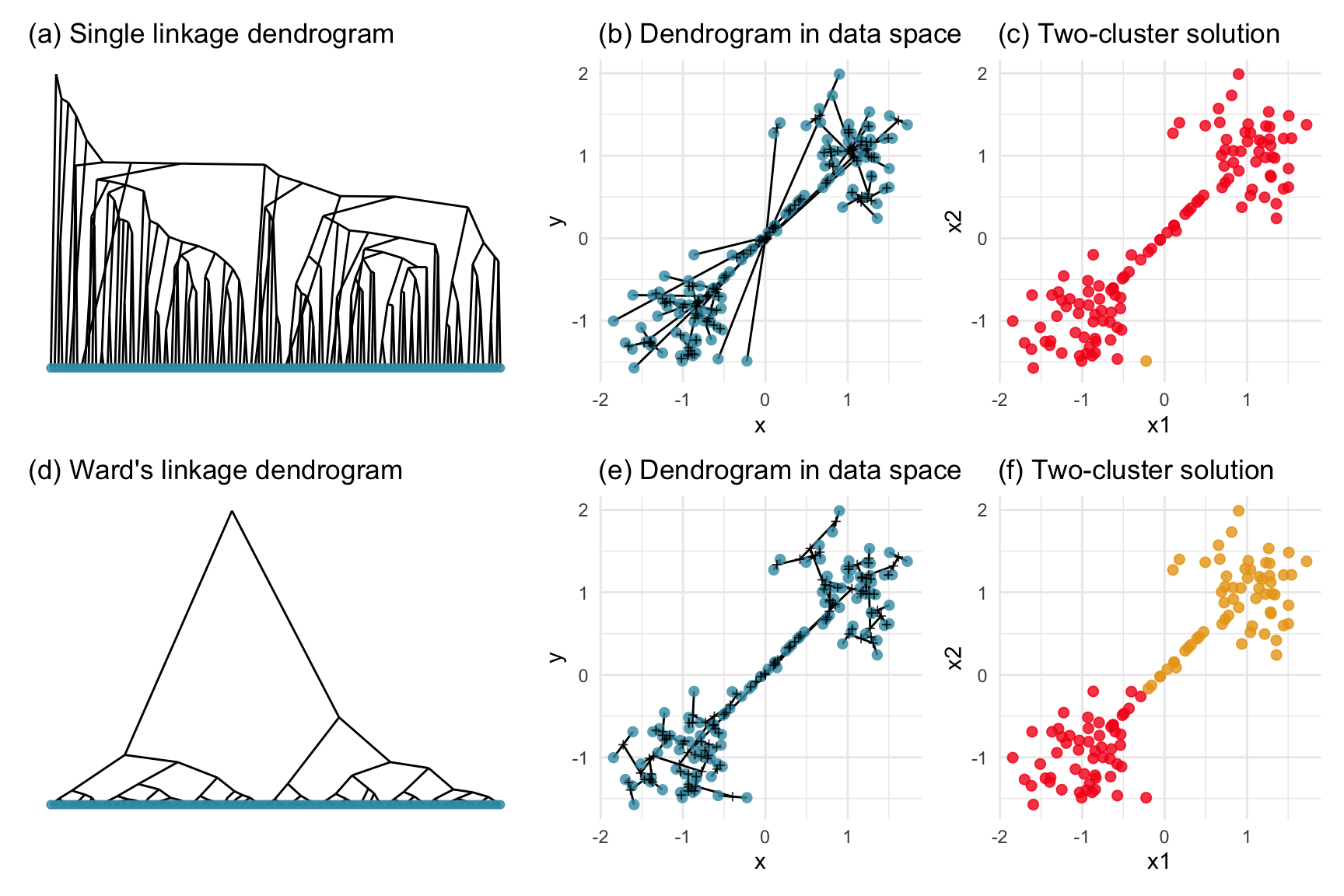
Figure 8.3: The effect of nuisance observations on single linkage (a, b, c) and Ward’s linkage hierarchical clustering (d, e, f). The single linkage dendrogram is very different to the Wards linkage dendrogram. When plotted with the data (b) we can see a pin cushion or asterisk pattern, where points are joined to others through a place in the middle of the line of nuisance observations. This results in the bad two cluster solution of a singleton cluster, and all the rest. Conversely, Ward’s dendrogram (d) strongly suggests two clusters, although the final join corresponds to just a small gap when shown on the data (e) but results in two sensible clusters.

Nuisance variables are ones that do not contribute to the clustering, such as x2 here. When we look at this data we see a gap between two elliptically shape clusters, with the gap being only in the horizontal direction, x1. When we compute the distances between points, in order to start clustering, without knowing that x2 is a nuisance variable, points across the gap might be considered to be closer than points within the same cluster. Figure 8.4 shows how nuisance variables affects complete linkage but not Wards linkage hierarchical clustering. (Wards linkage can be affected but it isn’t for this data.) Interestingly, the dendrogram for complete linkage looks ideal, that it suggests two clusters. It is not until you examine the resulting clusters in the data that you can see the error, that it has clustered across the gap.

Code
# Compute complete linkage
d2_hc <- hclust(dist(d2[,1:2]),
                method="complete")
d2_ggdc <- dendro_data(d2_hc, type = "triangle")
pd2c <- ggplot() +
  geom_segment(data=d2_ggdc$segments, 
               aes(x = x, y = y, 
                   xend = xend, yend = yend)) + 
  geom_point(data=d2_ggdc$labels, aes(x=x, y=y),
             colour="#3B99B1", alpha=0.8) +
  ggtitle("(a) Complete linkage dendrogram") +
  theme_minimal() +
  theme_dendro()

# Compute dendrogram in data
d2_hflyc <- hierfly(d2, d2_hc, scale=FALSE)

pd2hc <- ggplot() +
  geom_segment(data=d2_hflyc$segments, 
                aes(x=x, xend=xend,
                    y=y, yend=yend)) +
  geom_point(data=d2_hflyc$data, 
             aes(x=x1, y=x2,
                 shape=factor(node),
                 colour=factor(node),
                 size=1-node), alpha=0.8) +
  scale_shape_manual(values = c(16, 3)) +
  scale_colour_manual(values = c("#3B99B1", "black")) +
  scale_size(limits=c(0,17)) +
  ggtitle("(b) Dendrogram in data space") + 
  theme_minimal() +
  theme(aspect.ratio=1, legend.position="none")

# Show result
d2 <- d2 %>%
  mutate(clc = factor(cutree(d2_hc, 2)))
pc_d2c <- ggplot(d2) +
  geom_point(aes(x=x1, y=x2, colour=clc), 
             size=2, alpha=0.8) +
  scale_colour_discrete_divergingx(palette = "Zissou 1",
                                   nmax=4, rev=TRUE) +
  ggtitle("(c) Two-cluster solution") + 
  theme_minimal() +
  theme(aspect.ratio=1, legend.position="none")

# Compute Wards linkage
d2_hw <- hclust(dist(d2[,1:2]),
                method="ward.D2")
d2_ggdw <- dendro_data(d2_hw, type = "triangle")
pd2w <- ggplot() +
  geom_segment(data=d2_ggdw$segments, 
               aes(x = x, y = y, 
                   xend = xend, yend = yend)) + 
  geom_point(data=d2_ggdw$labels, aes(x=x, y=y),
             colour="#3B99B1", alpha=0.8) +
  ggtitle("(d) Ward's linkage dendrogram") +
  theme_minimal() +
  theme_dendro()

# Compute dendrogram in data
d2_hflyw <- hierfly(d2, d2_hw, scale=FALSE)

pd2hw <- ggplot() +
  geom_segment(data=d2_hflyw$segments, 
                aes(x=x, xend=xend,
                    y=y, yend=yend)) +
  geom_point(data=d2_hflyw$data, 
             aes(x=x1, y=x2,
                 shape=factor(node),
                 colour=factor(node),
                 size=1-node), alpha=0.8) +
  scale_shape_manual(values = c(16, 3)) +
  scale_colour_manual(values = c("#3B99B1", "black")) +
  scale_size(limits=c(0,17)) +
  ggtitle("(e) Dendrogram in data space") + 
  theme_minimal() +
  theme(aspect.ratio=1, legend.position="none")

# Show result
d2 <- d2 %>%
  mutate(clw = factor(cutree(d2_hw, 2)))
pc_d2w <- ggplot(d2) +
  geom_point(aes(x=x1, y=x2, colour=clw), 
             size=2, alpha=0.8) +
  scale_colour_discrete_divergingx(palette = "Zissou 1",
                                   nmax=4, rev=TRUE) +
  ggtitle("(f) Two-cluster solution") + 
  theme_minimal() +
  theme(aspect.ratio=1, legend.position="none")

pd2c + pd2hc + pc_d2c + 
  pd2w + pd2hw + pc_d2w +
  plot_layout(ncol=3)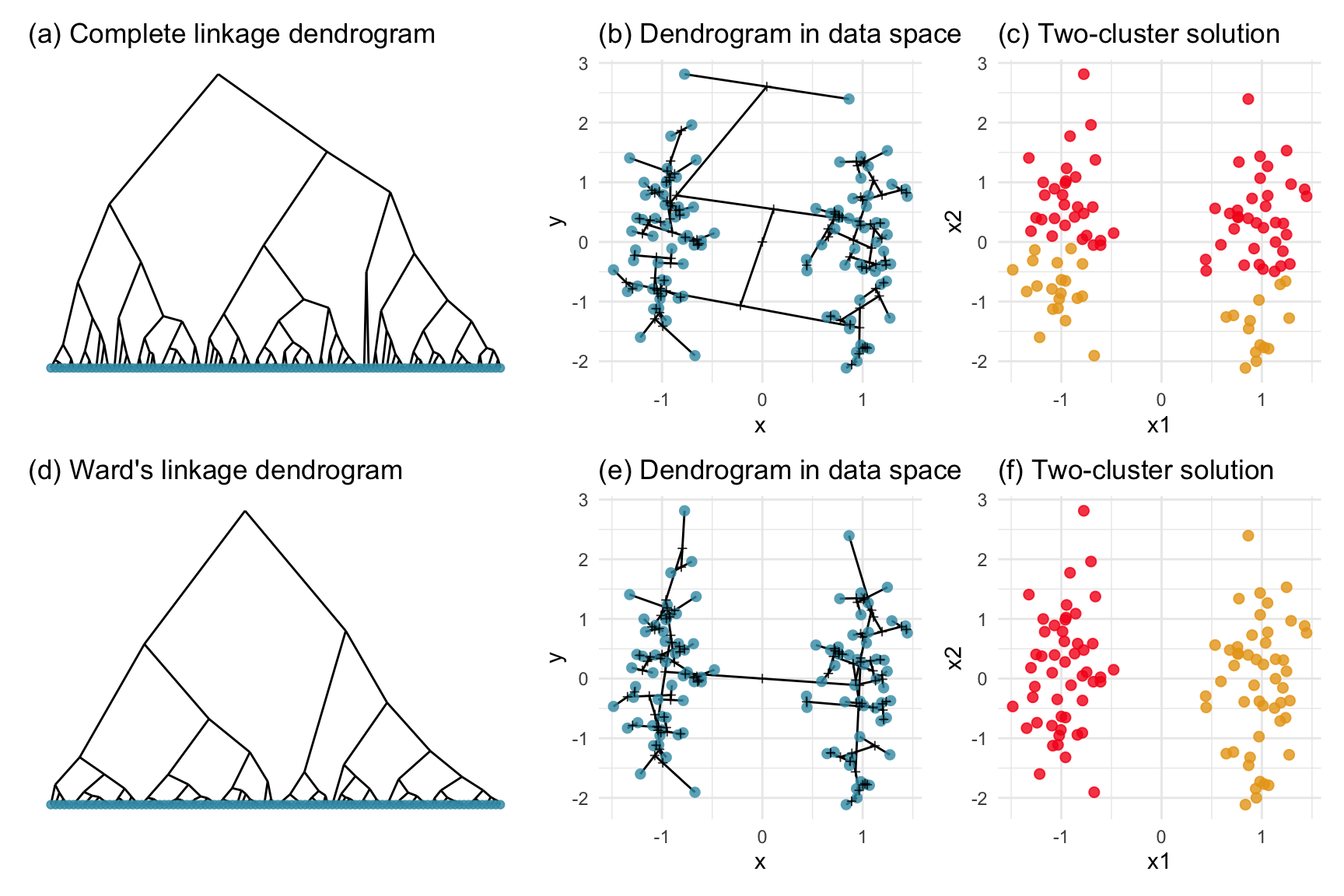
Figure 8.4: Complete linkage clustering (a, b, c) on nuisance variables in comparison to Ward’s linkage (d, e, f). The two dendrograms (a, d) look similar but when plotted on the data (b, e) we can see they are very different solutions. The complete linkage result breaks the data into clusters across the gap (c), which is a bad solution. It has been distract by the nuisance variables. Conversely, the Wards linkage two-cluster solution does as hoped, divided the data into two clusters separated by the gap (f).

Two dendrograms might look similar but the resulting clustering can be very different. They can also look very different but correspond to very similar clusterings. Plotting the dendrogram in the data space is important for understanding how the algorithm operated when grouping observations, even more so for high dimensions.

8.3 Dendrograms in high-dimensions

The first step with any clustering with high dimensional data is also to check the data. You typically don’t know whether there are clusters, or what shape they might be, or if there are nuisance observations or variables. A pairs plot like in Figure 8.5 is a nice complement to using the tour (Figure 8.6) for this. Here you can see three elliptical clusters, with one is further from the others.

Code for scatterplot matrix
load("data/penguins_sub.rda")
ggscatmat(penguins_sub[,1:4]) + 
  theme_minimal() +
  xlab("") + ylab("")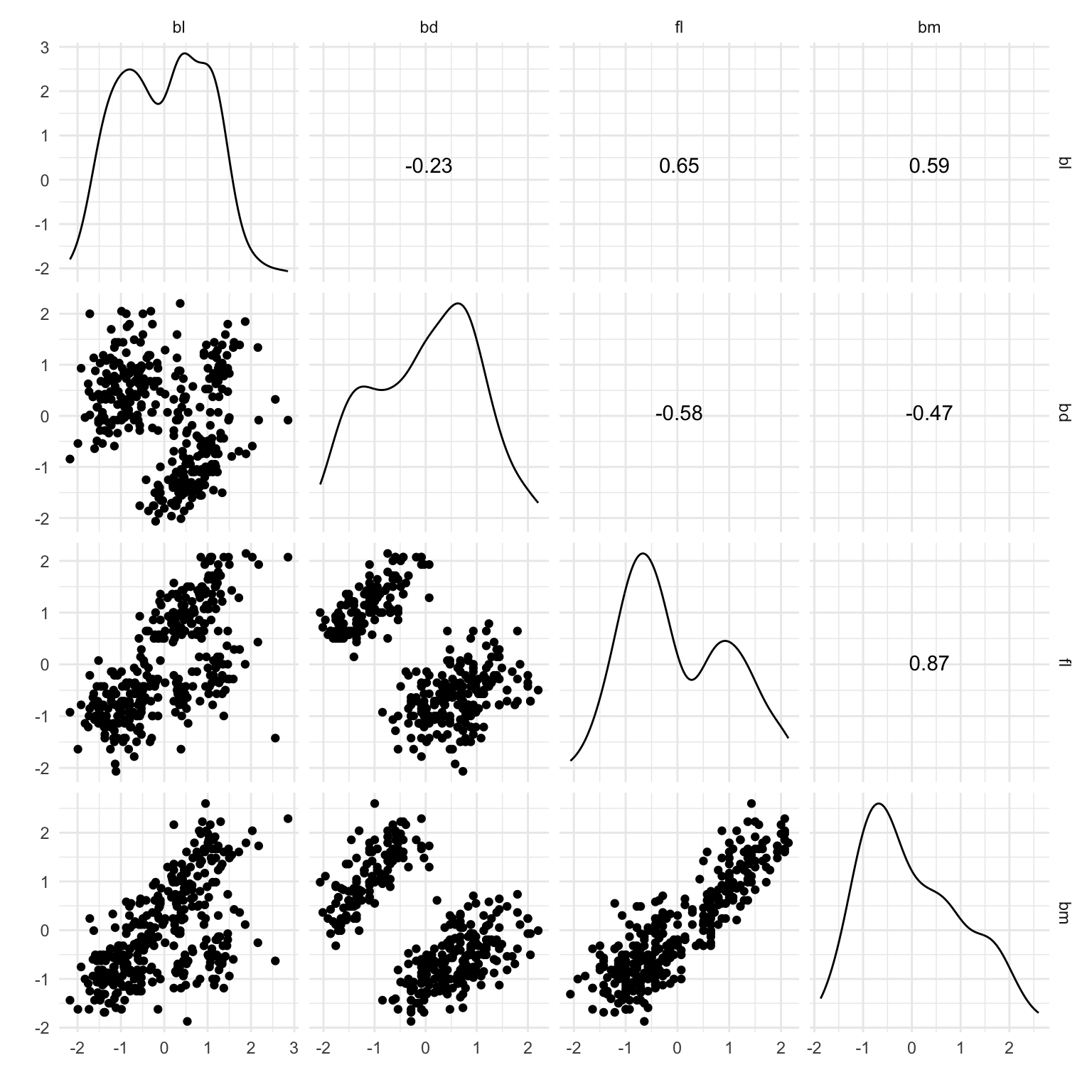
Figure 8.5: Make a scatterplot matrix to check for the presence of clustering, shape of clusters and presence of nuisance observations and variables. In the penguins it appears that there might be three elliptically shaped clusters, with some nuisance observations.
Code to create tour
set.seed(20230329)
b <- basis_random(4,2)
pt1 <- save_history(penguins_sub[,1:4], 
                    max_bases = 500, 
                    start = b)
save(pt1, file="data/penguins_tour_path.rda")

# To re-create the gifs
load("data/penguins_tour_path.rda")
animate_xy(penguins_sub[,1:4], 
           tour_path = planned_tour(pt1), 
           axes="off", rescale=FALSE, 
           half_range = 3.5)

render_gif(penguins_sub[,1:4], 
           planned_tour(pt1), 
           display_xy(half_range=0.9, axes="off"),
           gif_file="gifs/penguins_gt.gif",
           frames=500,
           loop=FALSE)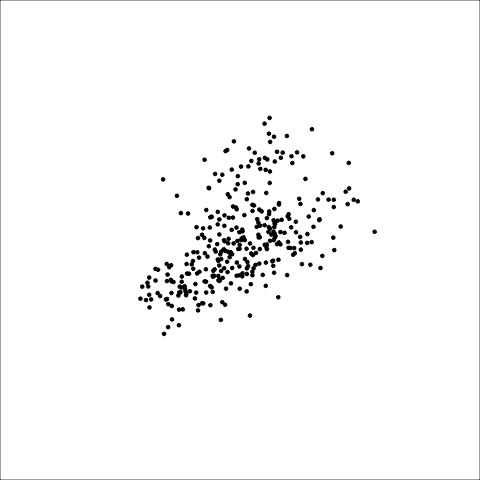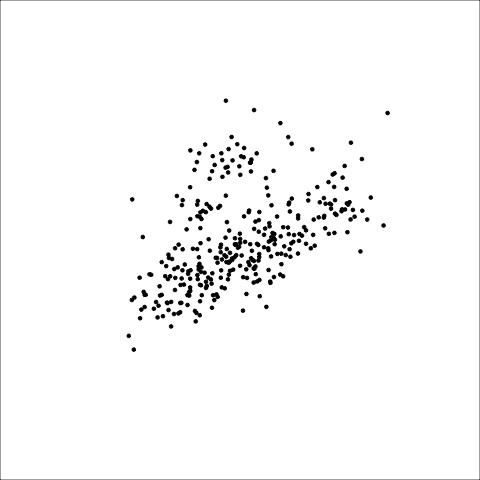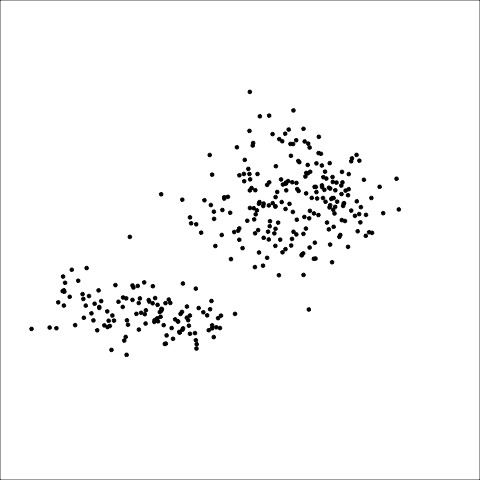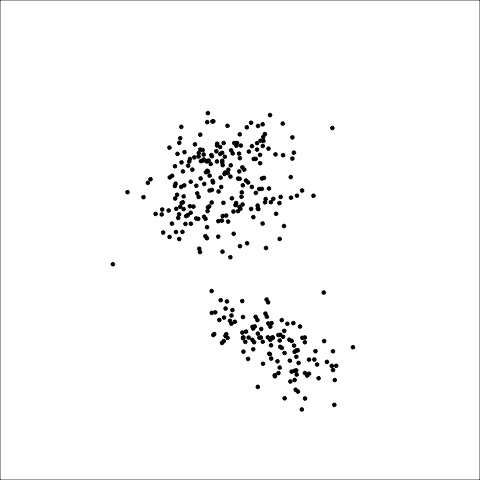
Tour of many linear projections of the penguins data. You can see three elliptical clusters, one further apart from the other two.
Figure 8.6: Use a grand tour of your data to check for clusters, the shape of clusters and for nuisance observations and variables. Here the penguins data looks like it has possibly three elliptical clusters, one more separated than the other two, with some nuisance observations.

The process is the same as for the simpler example. We compute and draw the dendrogram in 2D, compute it in \(p\)-D and view with a tour. Here we have also chosen to examine the three cluster solution for single linkage and wards linkage clustering.

p_dist <- dist(penguins_sub[,1:4])
p_hcw <- hclust(p_dist, method="ward.D2")
p_hcs <- hclust(p_dist, method="single")

p_clw <- penguins_sub %>% 
  mutate(cl = factor(cutree(p_hcw, 3))) %>%
  as.data.frame()
p_cls <- penguins_sub %>% 
  mutate(cl = factor(cutree(p_hcs, 3))) %>%
  as.data.frame()

p_w_hfly <- hierfly(p_clw, p_hcw, scale=FALSE)
p_s_hfly <- hierfly(p_cls, p_hcs, scale=FALSE)
Code to draw dendrograms
# Generate the dendrograms in 2D
p_hcw_dd <- dendro_data(p_hcw)
pw_dd <- ggplot() +
  geom_segment(data=p_hcw_dd$segments, 
               aes(x = x, y = y, 
                   xend = xend, yend = yend)) + 
  geom_point(data=p_hcw_dd$labels, aes(x=x, y=y),
             alpha=0.8) +
  theme_dendro()

p_hcs_dd <- dendro_data(p_hcs)
ps_dd <- ggplot() +
  geom_segment(data=p_hcs_dd$segments, 
               aes(x = x, y = y, 
                   xend = xend, yend = yend)) + 
  geom_point(data=p_hcs_dd$labels, aes(x=x, y=y),
             alpha=0.8) +
  theme_dendro()
Code to create tours of dendrogram in data
load("data/penguins_tour_path.rda")
glyphs <- c(16, 46)
pchw <- glyphs[p_w_hfly$data$node+1]
pchs <- glyphs[p_s_hfly$data$node+1]

animate_xy(p_w_hfly$data[,1:4], 
           #col=colw, 
           tour_path = planned_tour(pt1),
           pch = pchw,
           edges=p_w_hfly$edges, 
           axes="bottomleft")

animate_xy(p_s_hfly$data[,1:4], 
           #col=colw, 
           tour_path = planned_tour(pt1),
           pch = pchs,
           edges=p_s_hfly$edges, 
           axes="bottomleft")

render_gif(p_w_hfly$data[,1:4], 
           planned_tour(pt1),
           display_xy(half_range=0.9,            
                      pch = pchw,
                      edges = p_w_hfly$edges,
                      axes = "off"),
           gif_file="gifs/penguins_hflyw.gif",
           frames=500,
           loop=FALSE)

render_gif(p_s_hfly$data[,1:4], 
           planned_tour(pt1), 
           display_xy(half_range=0.9,            
                      pch = pchs,
                      edges = p_s_hfly$edges,
                      axes = "off"),
           gif_file="gifs/penguins_hflys.gif",
           frames=500,
           loop=FALSE)

# Show three cluster solutions
clrs <- hcl.colors(3, "Zissou 1")
w3_col <- clrs[p_w_hfly$data$cl[p_w_hfly$data$node == 0]]
render_gif(p_w_hfly$data[p_w_hfly$data$node == 0, 1:4], 
           planned_tour(pt1), 
           display_xy(half_range=0.9,   
                      col=w3_col,
                      axes = "off"),
           gif_file="gifs/penguins_w3.gif",
           frames=500,
           loop=FALSE)

s3_col <- clrs[p_s_hfly$data$cl[p_w_hfly$data$node == 0]]
render_gif(p_s_hfly$data[p_w_hfly$data$node == 0,1:4], 
           planned_tour(pt1), 
           display_xy(half_range=0.9,   
                      col=s3_col,
                      axes = "off"),
           gif_file="gifs/penguins_s3.gif",
           frames=500,
           loop=FALSE)

Figure 8.7 and Figure 8.8 show results for single linkage and wards linkage clustering of the penguins data. fig-penguins-ddw shows the 2D dendrograms. The 2D dendrograms are very different. Wards linkage produces a clearer indication of clusters, with a suggestion of three, or possibly four or five clusters. The dendrogram for single linkage suggests two clusters, and has the classical waterfall appearance that is often seen with this type of linkage. (If you look carefully, though, you will see it is actually a three cluster solution. At the very top of the dendrogram there is another branch connecting one observation to the other two clusters.)

Figure 8.8 (a) and (b) show the dendrograms in 4D overlaid on the data. The two are starkly different. The single linkage clustering is like pins pointing to (three) centres, with some long extra edges.

Plots (c) and (d) show the three cluster solutions, with Wards linkage almost recovering the clusters of the three species. Single linkage has two big clusters, and the singleton cluster. Although the Wards linkage produces the best result, single linkage does provide some interesting and useful information about the data. That singleton cluster is an outlier, an unusually-sized penguin. We can see it as an outlier just from the tour in Figure 8.6 but single linkage emphasizes it, bringing it more strongly to our attention.

Figure 8.7: Wards linkage (left) and single linkage (right).
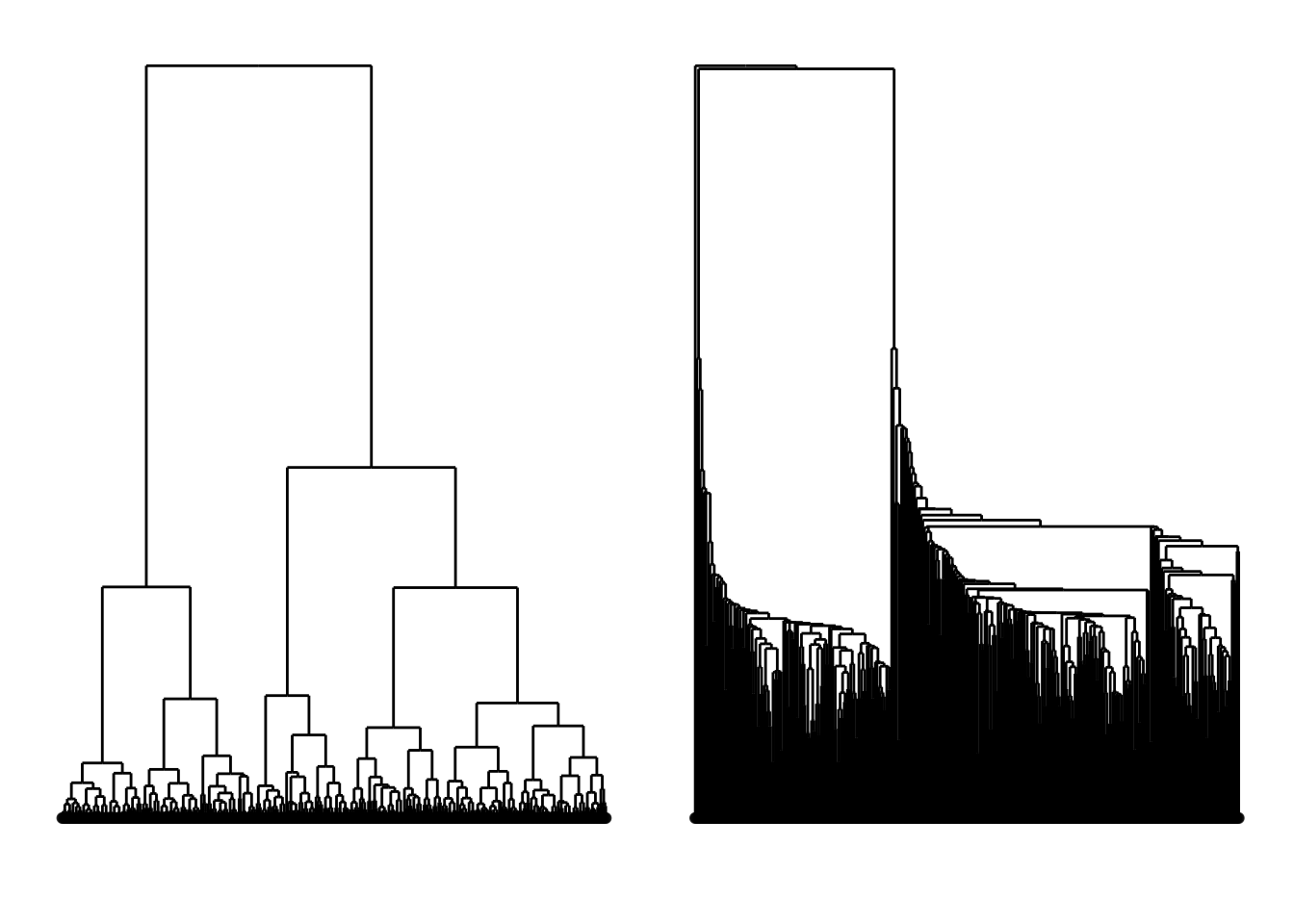
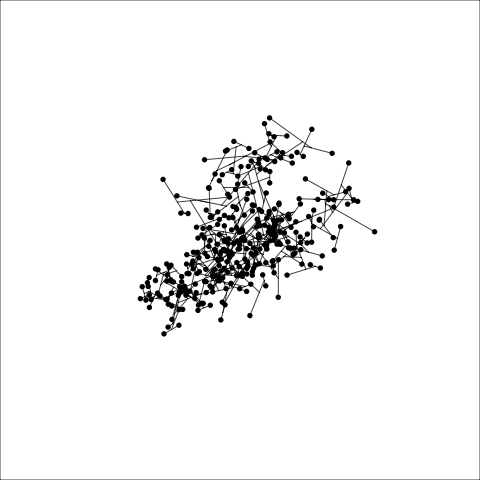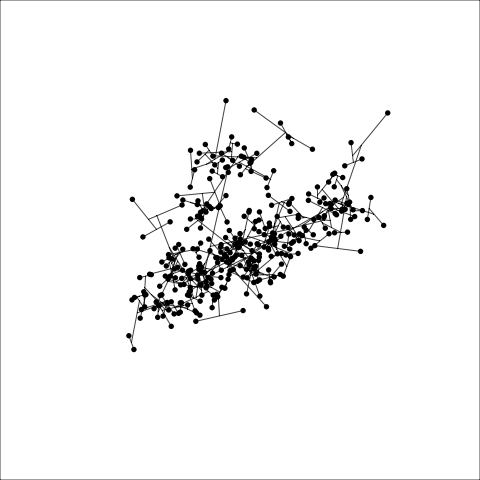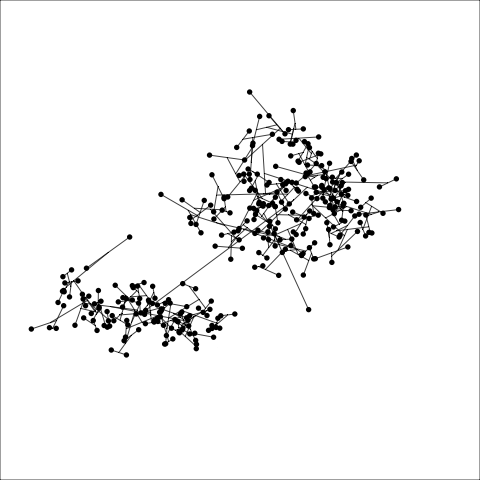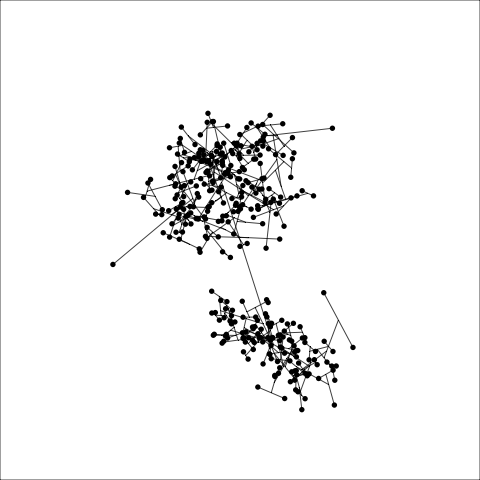
Tour showing the dendrogram for Wards linkage clustering on the penguins data in 4D. You can see that it connects points within each clump and then connects between clusters.
(a) Wards linkage
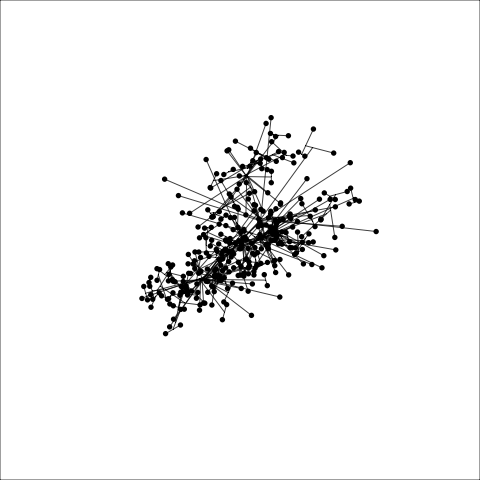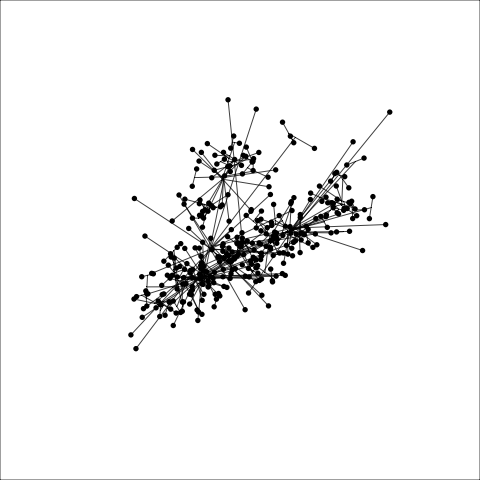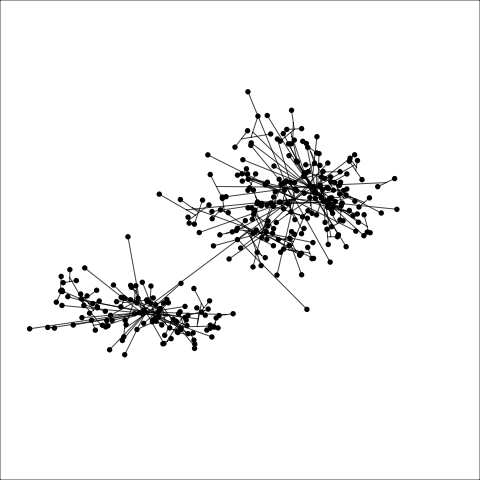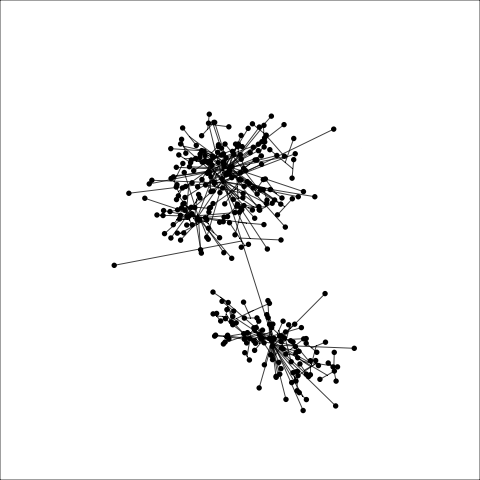
Tour showing the dendrogram for single linkage clustering on the penguins data in 4D. You can see that the connections are like asterisks, connecting towards the center of each clump and there are a couple of long connections between clusters.
(b) Single linkage
(c) Wards linkage
(d) Single linkage
Figure 8.8: Dendrograms for Wards and single linkage of the penguins data, shown in 2D (top) and in 4D (middle), and the three-cluster solution of each.

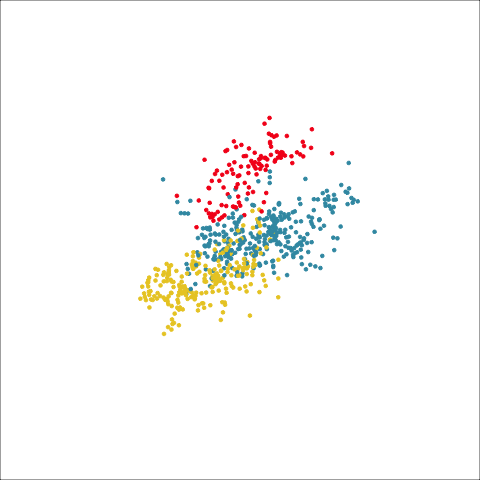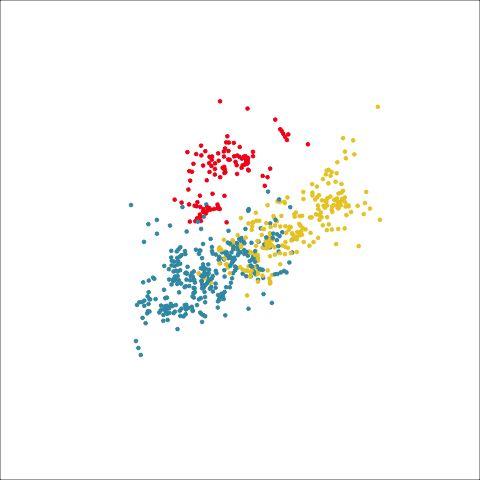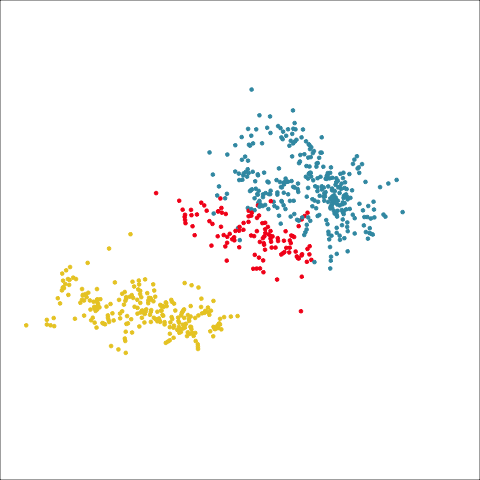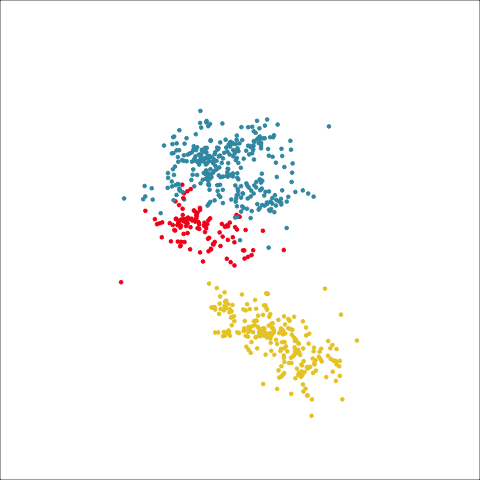
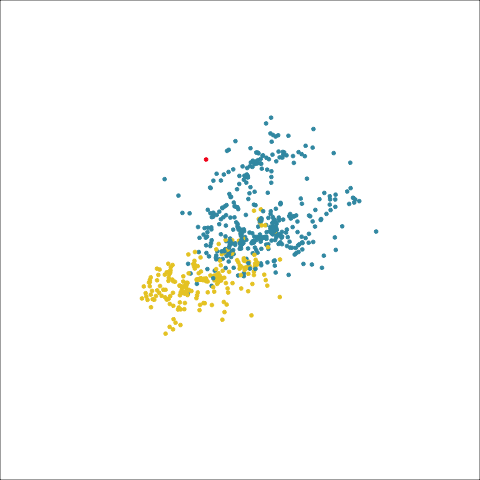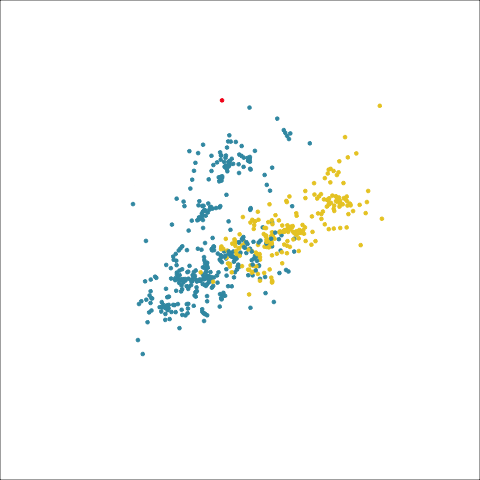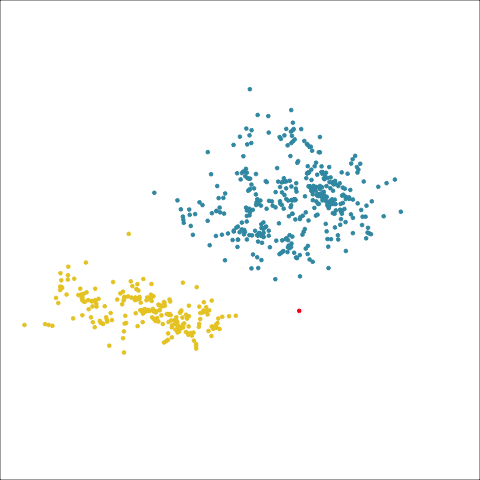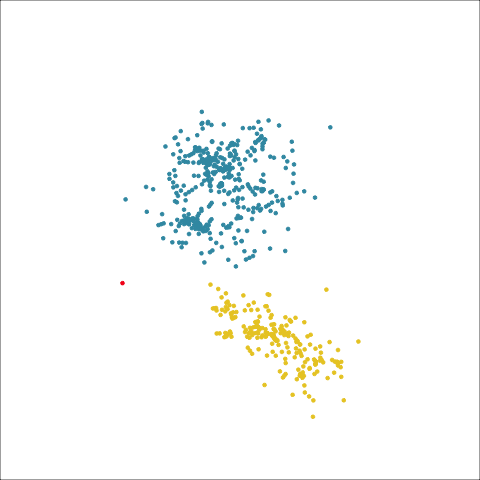
Single linkage on the penguins has a very different joining pattern to Wards! While Wards provides the better result, single linkage provides useful information about the data, such as emphasizing the outlier.

Figure 8.9 provides HTML objects of the dendrograms, so that they can be directly compared. The same tour path is used, so the sliders allow setting the view to the same projection in each plot.

Code to make html objects of the dendrogram in 4D
load("data/penguins_tour_path.rda")
# Create a smaller one, for space concerns
pt1i <- interpolate(pt1[,,1:5], 0.1)
pw_anim <- render_anim(p_w_hfly$data,
                       vars=1:4,
                       frames=pt1i, 
                       edges = p_w_hfly$edges,
             obs_labels=paste0(1:nrow(p_w_hfly$data),
                               p_w_hfly$data$cl))

pw_gp <- ggplot() +
     geom_segment(data=pw_anim$edges, 
                    aes(x=x, xend=xend,
                        y=y, yend=yend,
                        frame=frame)) +
     geom_point(data=pw_anim$frames, 
                aes(x=P1, y=P2, 
                    frame=frame, 
                    shape=factor(node),
                    label=obs_labels), 
                alpha=0.8, size=1) +
     xlim(-1,1) + ylim(-1,1) +
     scale_shape_manual(values=c(16, 46)) +
     coord_equal() +
     theme_bw() +
     theme(legend.position="none", 
           axis.text=element_blank(),
           axis.title=element_blank(),
           axis.ticks=element_blank(),
           panel.grid=element_blank())

pwg <- ggplotly(pw_gp, width=450, height=500,
                tooltip="label") %>%
       animation_button(label="Go") %>%
       animation_slider(len=0.8, x=0.5,
                        xanchor="center") %>%
       animation_opts(easing="linear", transition = 0)
htmlwidgets::saveWidget(pwg,
          file="html/penguins_cl_ward.html",
          selfcontained = TRUE)

# Single
ps_anim <- render_anim(p_s_hfly$data, vars=1:4,
                         frames=pt1i, 
                       edges = p_s_hfly$edges,
             obs_labels=paste0(1:nrow(p_s_hfly$data),
                               p_s_hfly$data$cl))

ps_gp <- ggplot() +
     geom_segment(data=ps_anim$edges, 
                    aes(x=x, xend=xend,
                        y=y, yend=yend,
                        frame=frame)) +
     geom_point(data=ps_anim$frames, 
                aes(x=P1, y=P2, 
                    frame=frame, 
                    shape=factor(node),
                    label=obs_labels), 
                alpha=0.8, size=1) +
     xlim(-1,1) + ylim(-1,1) +
     scale_shape_manual(values=c(16, 46)) +
     coord_equal() +
     theme_bw() +
     theme(legend.position="none", 
           axis.text=element_blank(),
           axis.title=element_blank(),
           axis.ticks=element_blank(),
           panel.grid=element_blank())

psg <- ggplotly(ps_gp, width=450, height=500,
                tooltip="label") %>%
       animation_button(label="Go") %>%
       animation_slider(len=0.8, x=0.5,
                        xanchor="center") %>%
       animation_opts(easing="linear", transition = 0)
htmlwidgets::saveWidget(psg,
          file="html/penguins_cl_single.html",
          selfcontained = TRUE)
Figure 8.9: Animation of dendrogram from Wards (top) and single (bottom) linkage clustering of the penguins data.

Viewing the dendrograms in high-dimensions provides insight into how the observations have joined points to clusters. For example, single linkage often has edges leading to a single focal point, which might not be yield a useful clustering but might help to identify outliers. If the edges point to multiple focal points, with long edges bridging gaps in the data, the result is more likely yielding a useful clustering.

Exercises

  1. Compute complete linkage clustering for the nuisance observations data set. Does it perform more similarly to single linkage or Wards linkage?
  2. Compute single linkage clustering for the nuisance variables data. Does it perform more similarly to complete linkage or Wards linkage?
  3. Use hierarchical clustering with Euclidean distance and Wards linkage to split the clusters_nonlin data into four clusters. Look at the dendrogram in 2D and 4D. In 4D you can also include the cluster assignment as color. Does this look like a good solution?
  4. Repeat the same exercise using single linkage instead of Wards linkage. How does this solution compare to what we have found with Wards linkage? Does the solution match how you would cluster the data in a spin-and-brush approach?
  5. Argue why single linkage might not perform well for the fake_trees data. Which method do you think will work best with this data? Conduct hierarchical clustering with your choice of linkage method. Does the 2D dendrogram suggest 10 clusters for the 10 branches? Take a look at the high-dimensional representation of the dendrogram. Has your chosen method captured the branches well, or not, explaining what you think worked well or poorly?
  6. What would a useful clustering of the first four PCs of the aflw data be? What linkage method would you expect works best to cluster it this way? Conduct the clustering. Examine the 2D dendrogram and decide on how many clusters should be used. Examine the cluster solution using a tour with points coloured by cluster.
  7. Based on your assessment of the cluster structure in the challenge data sets, c1-c7, from the mulgar package, which linkage method would you recommend. Use your suggested linkage method to cluster each data set, and summarise how well it performed in detecting the clusters that you have seen.