Creating effective data plots

Dianne Cook
Monash University

Why (1/3)

Is there any pattern in the residuals that indicate a problem with the model fit?

Do we need to change the model specification?

Why (2/3)

Is there a difference between the species?

Why (3/3)

Which is the best display to answer: what is distribution of thyroid cancer across Australia?

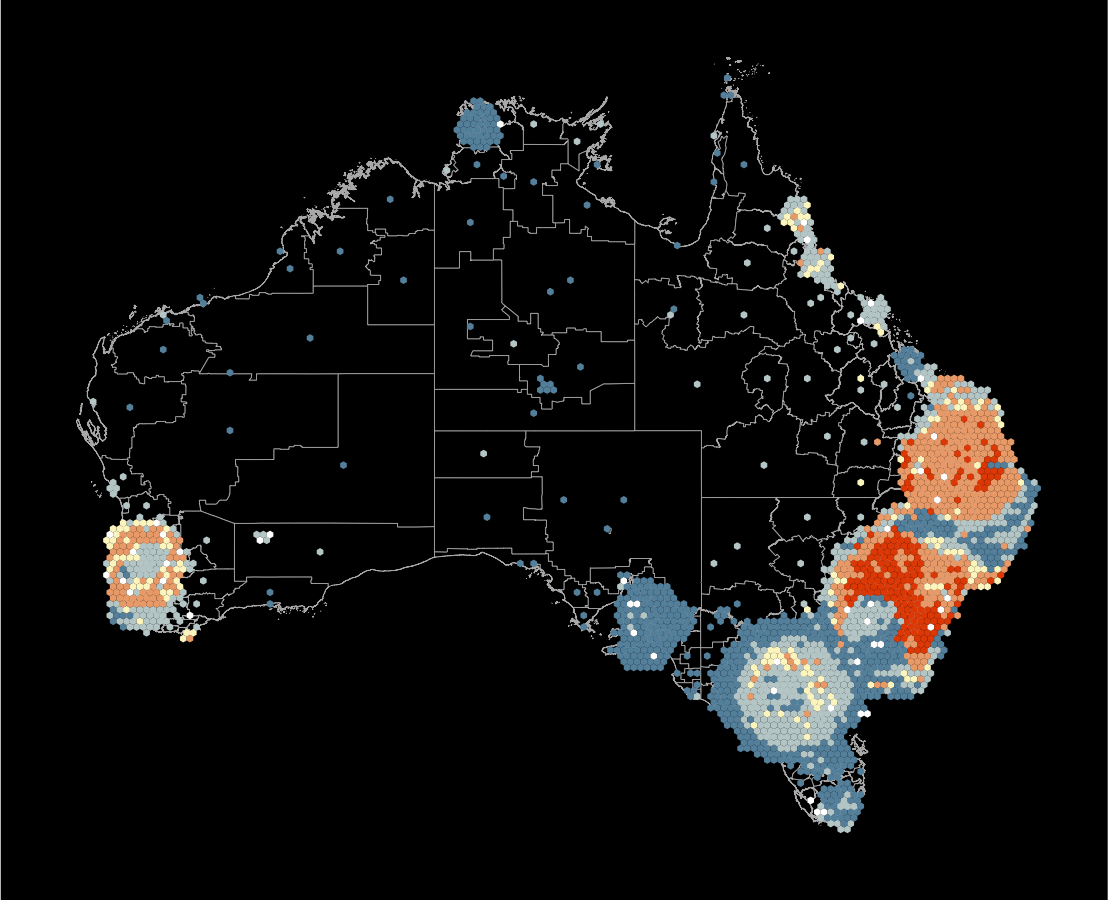
What’s the goal?

Reading data plots is subjective.

Making decisions based on data visualisations is common, where we need to be objective .

It is possible, and here is how we do that …

Outline

• Organising your data into tidy form
• Mapping the variables to elements of the plot
• Cognitive principles: briefly
• Testing the strength of patterns in the plot
• Testing which is the best design

These are the tools you need

install.packages("ggplot2")

or better yet:

install.packages("tidyverse")

• Define your plots using a grammar that maps variables in tidy data to elements of the plot.
• Wrangle your data into tidy form for clarity of plot specification.

space

install.packages("nullabor")

• Compare your data plot to plots of null data.
• This checks whether what we see is real or spurious.
• Also allows for measuring the effectiveness of one plot design vs another.

Organising your data to enable mapping variables to graphical elements

Tidy data

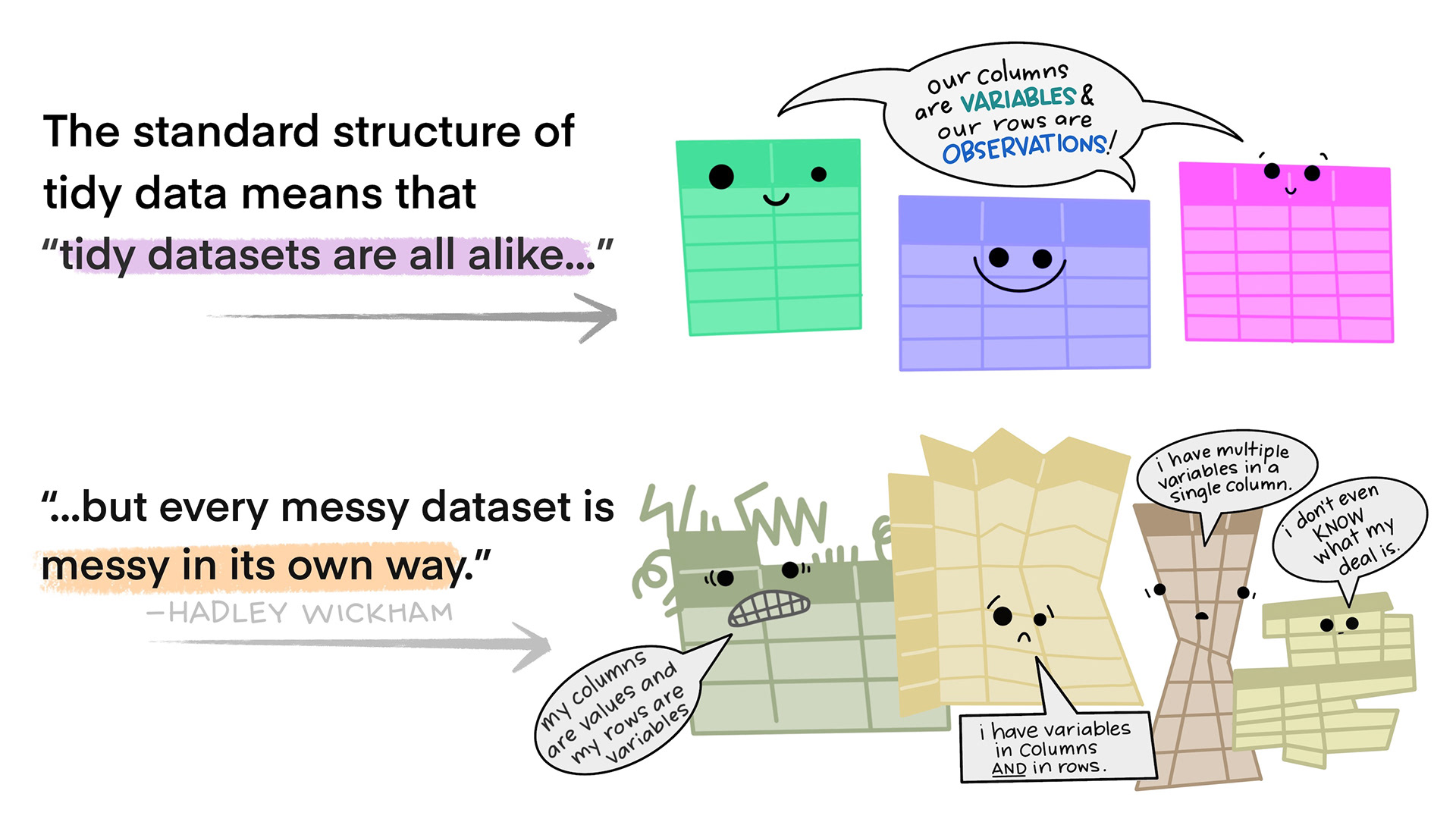
1. Each variable forms a column
2. Each observation forms a row
3. Each type of observational unit forms a table. If you have data on multiple levels (e.g. data about houses and data about the rooms within those houses), these should be in separate tables.

Illustrations from the Openscapes blog Tidy Data for reproducibility, efficiency, and collaboration by Julia Lowndes and Allison Horst

QUESTION

How would you get this data into tidy form?

Tuberculosis from WHO

Tidying

First get the data in tidy form

tb_aus_sa <- tb_aus |>
  filter(year > 2012) |>
  select(iso3, year, 
         newrel_f014:newrel_f65, 
         newrel_m014:newrel_m65) |>
  pivot_longer(cols=newrel_f014:newrel_m65,
               names_to = "sex_age", 
               values_to = "count") |>
  filter(!is.na(count)) |>
  separate(sex_age, into=c("stuff", 
                           "sex_age")) |>
  mutate(sex = str_sub(sex_age, 1, 1),
         age = str_sub(sex_age, 2, 
                       str_length(sex_age))) |>
  mutate(age = case_when(
    age == "014" ~ "0-14",
    age == "1524" ~ "15-24",
    age == "2534" ~ "25-34",
    age == "3544" ~ "35-44",
    age == "4554" ~ "45-54",
    age == "5564" ~ "55-64",
    age == "65" ~ "65")) |>
  select(iso3, year, sex, age, count)

Statistical data

\[X = \left[ \begin{array}{rrrr} X_{~1} & X_{~2} & ... & X_{~p} \end{array} \right] \\ = \left[ \begin{array}{rrrr} X_{~11} & X_{~12} & ... & X_{~1p} \\ X_{~21} & X_{~22} & ... & X_{~2p} \\ \vdots & \vdots & \ddots& \vdots \\ X_{~n1} & X_{~n2} & ... & X_{~np} \end{array} \right]\]

• This is tidy data!
• You might also make assumptions about the distribution of each variable, e.g. \(X_{~1} \sim N(0,1), ~~X_{~2} \sim \text{Exp}(1) ...\)

Mapping

In ggplot2, the variables from tidy data are explicitly mapped to elements of the plot, using aesthetics.

Basic Mappings

• x and y to plot points in a two-dimensional space
• color, fill to render as a color scale
• size maps variable to size of object
• shape maps variable to different shapes

Depending on the geom different mappings are possible, xmin, xend, linetype, alpha, stroke, weight …

Facets

Variables are used to subset (or condition)

Layers

Different data can be mapped onto the same plot, eg observations, and means

Example

ggplot(mpg, 
       aes(
         x=displ, 
         y=hwy, 
         color=class)) + 
  geom_point()

displ is mapped to x
hwy is mapped to y
class is mapped to color.

Common plot descriptions as scripts

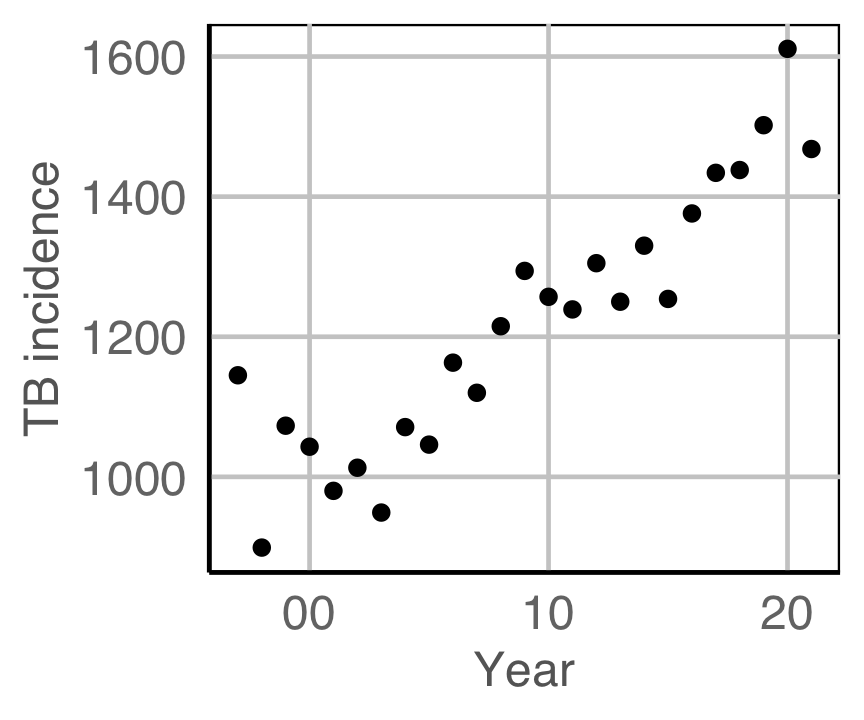
Example 1A

How are variables mapped to create this plot?

ggplot(tb_aus, 
       aes(x=year, 
           y=c_newinc)) + 
  geom_point() +
  scale_x_continuous("Year", 
    breaks = seq(1980, 2020, 10), 
    labels = c("80", "90", "00", "10", "20")) +
  ylab("TB incidence") 

Example 1B

How are variables mapped to create this plot?

ggplot(tb_aus, 
       aes(x=year, 
       y=c_newinc)) + 
  geom_point() +
  geom_smooth(se=F, colour="#F5191C") +
  scale_x_continuous("Year", breaks = seq(1980, 2020, 10), labels = c("80", "90", "00", "10", "20")) +
  ylab("TB incidence") 

Example 2A

How are variables mapped to create this plot?

ggplot(penguins, 
       aes(x=flipper_length_mm, 
           y=bill_length_mm, 
           color=species)) + 
  geom_point(alpha=0.8) +
  scale_color_discrete_divergingx(palette="Zissou 1") +
  theme(legend.title = element_blank(), 
        legend.position = "bottom",
        legend.direction = "horizontal",
        legend.text = element_text(size="8"))

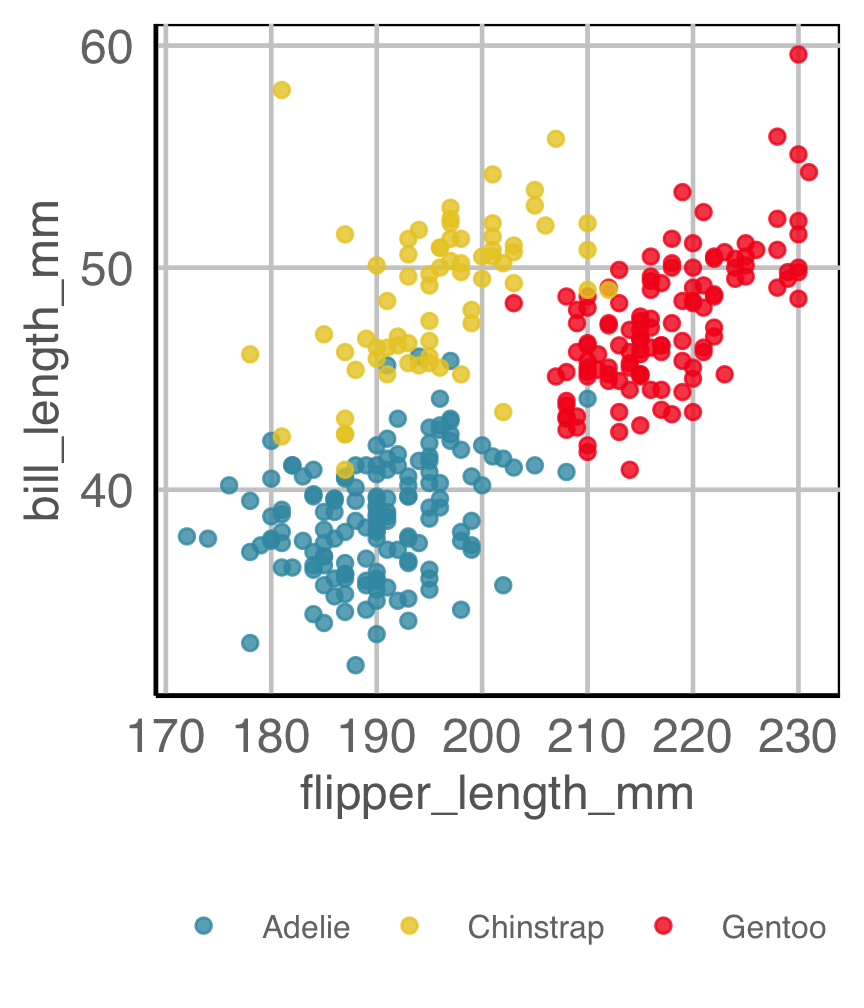
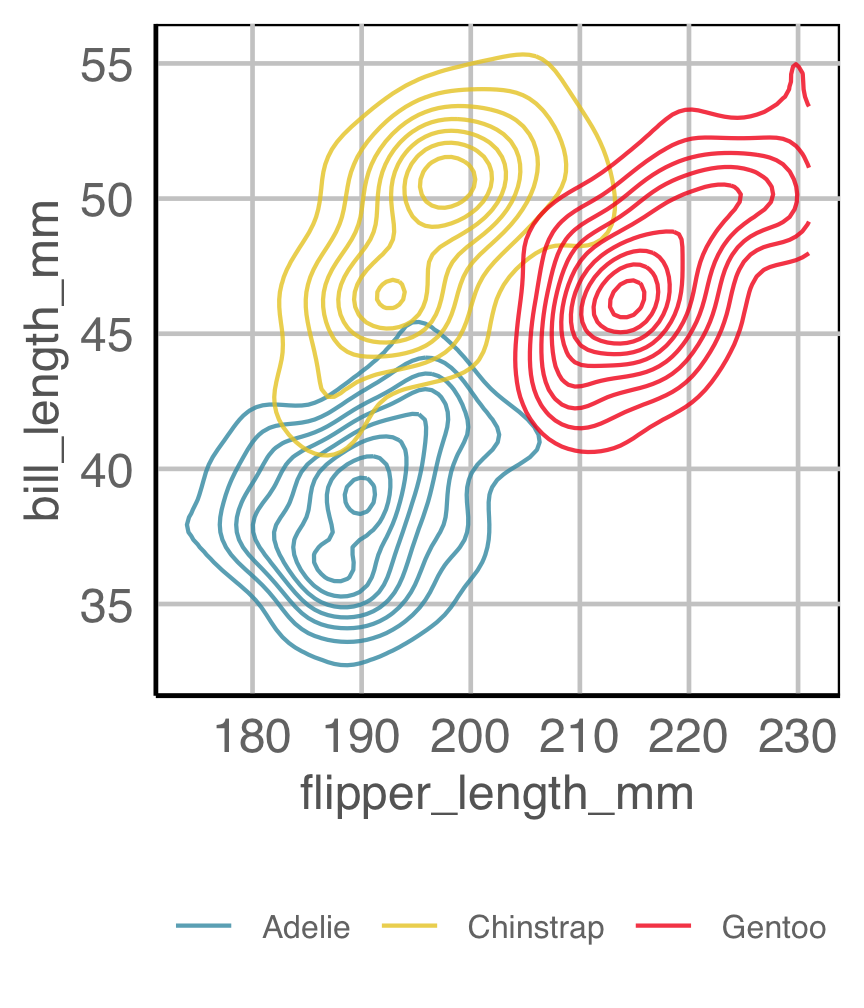
Example 2B

How are variables mapped to create this plot?

ggplot(penguins, 
       aes(x=flipper_length_mm, 
           y=bill_length_mm, 
           color=species)) + 
  geom_density2d(alpha=0.8) +
  scale_color_discrete_divergingx(palette="Zissou 1") +
  theme(legend.title = element_blank(), 
        legend.position = "bottom",
        legend.direction = "horizontal",
        legend.text = element_text(size="8"))

Easily re-plot different ways (1/2)

ggplot(tb_aus_sa, 
       aes(x=year, 
           y=count, 
           fill=sex)) + 
  geom_col(position="fill") +
  facet_wrap(~age, ncol=7) +
  ylab("") +
  scale_fill_discrete_divergingx(palette="ArmyRose") +
  scale_x_continuous("year", 
    breaks = seq(2013, 2021, 2), 
    labels = c("13", "15", "17", "19", "21")) +
  theme(legend.position = "bottom", 
        legend.direction = "horizontal",
        legend.title = element_blank(),
        axis.text = element_text(size="10"))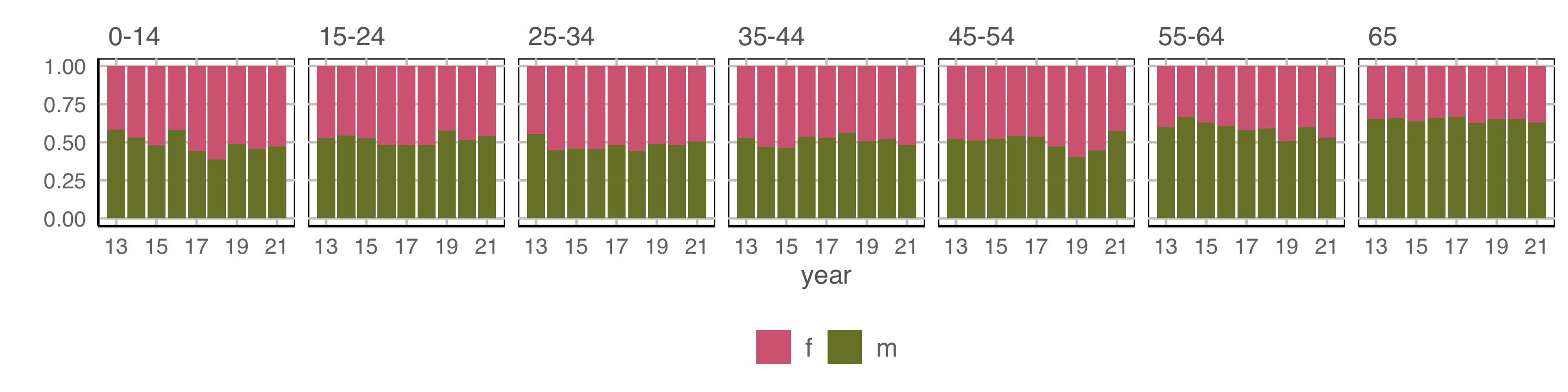

Observations: Relatively equal proportions, with more incidence among males in older population. No clear temporal trend.

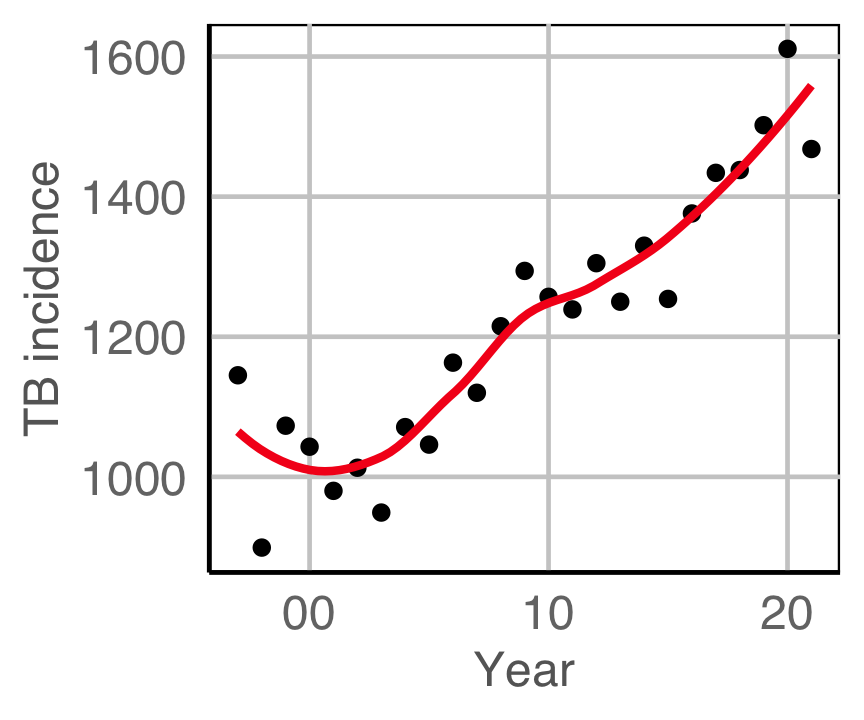
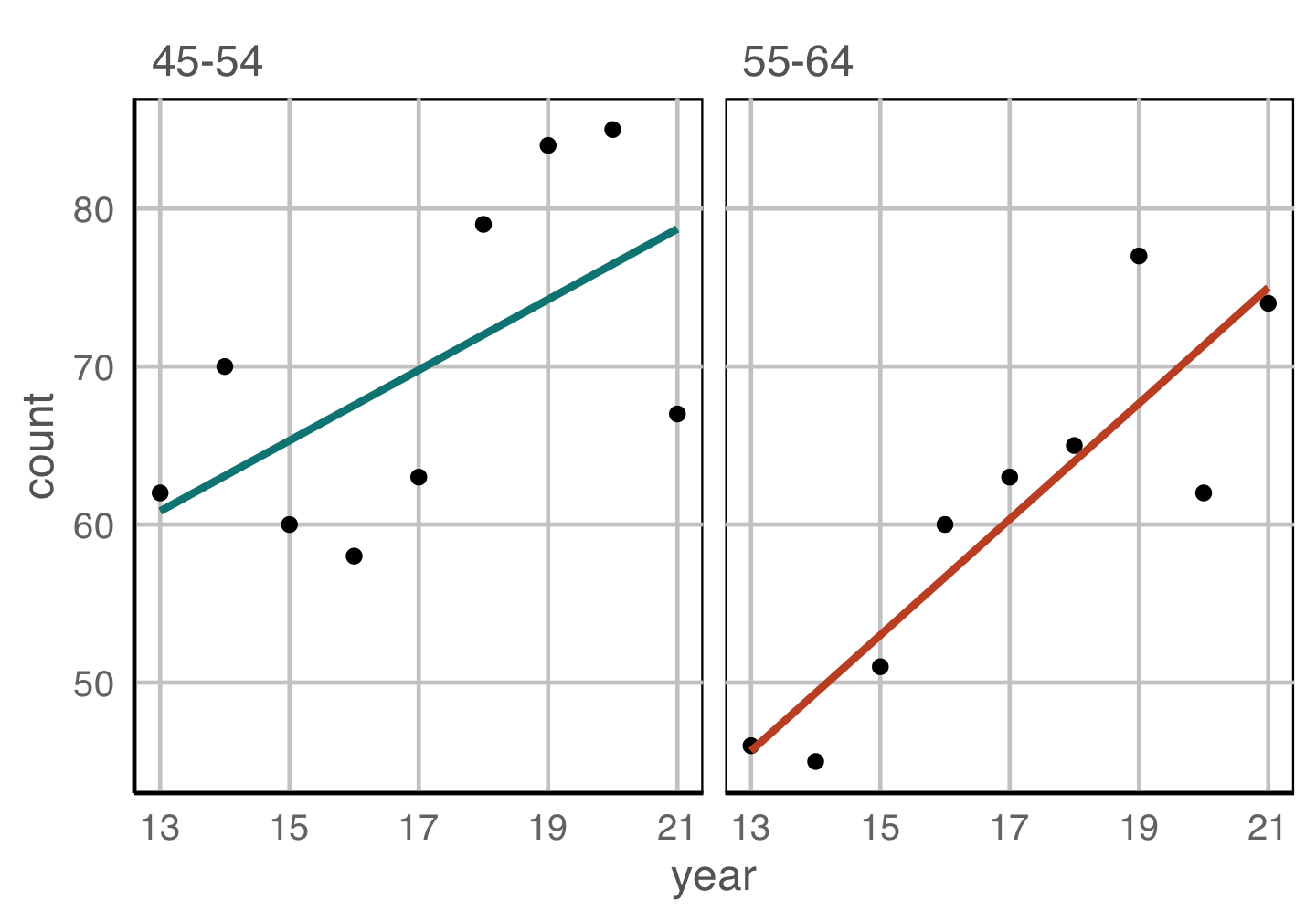
Easily re-plot different ways (2/2)

ggplot(tb_aus_sa, 
       aes(x=year, 
           y=count, 
           colour=sex)) + 
  geom_point() +
  geom_smooth(se=F, alpha=0.7) +
  facet_grid(sex~age, scales = "free_y") +
  ylab("count") +
  scale_colour_discrete_divergingx(palette="ArmyRose") +
  scale_x_continuous("year", 
    breaks = seq(2013, 2021, 2), 
    labels = c("13", "15", "17", "19", "21")) +
  theme(legend.position = "bottom", 
        legend.direction = "horizontal",
        legend.title = element_blank(),
        axis.text = element_text(size="10"))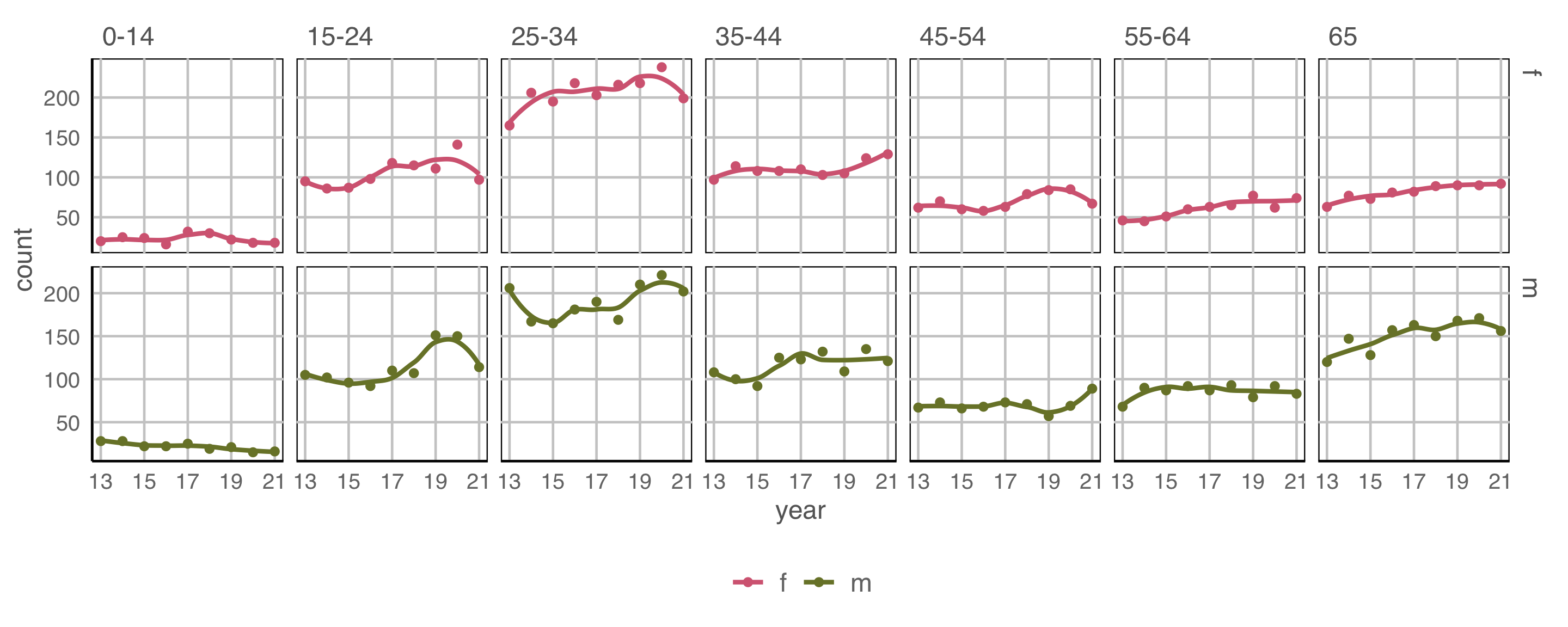

Small increasing temporal trend is present in early age groups, for both males and females. Also older groups, although numbers are much smaller.

Tidy data to plot descriptions allows quick re-arrangment, and clearly shows relationship between plots

Cognitive principles

Hierarchy of mappings

Cleveland and McGill (1984)

Illustrations made by Emi Tanaka

Hierarchy of mappings

1. Position - common scale (BEST)
2. Position - nonaligned scale
3. Length, direction, angle
4. Area
5. Volume, curvature
6. Shading, color (WORST)

1. scatterplot, barchart
2. side-by-side boxplot, stacked barchart
3. piechart, rose plot, gauge plot, donut, wind direction map, starplot
4. treemap, bubble chart, mosaicplot
5. chernoff face
6. choropleth map

Proximity

Place elements that you want to compare close to each other. If there are multiple comparisons to make, you need to decide which one is most important.

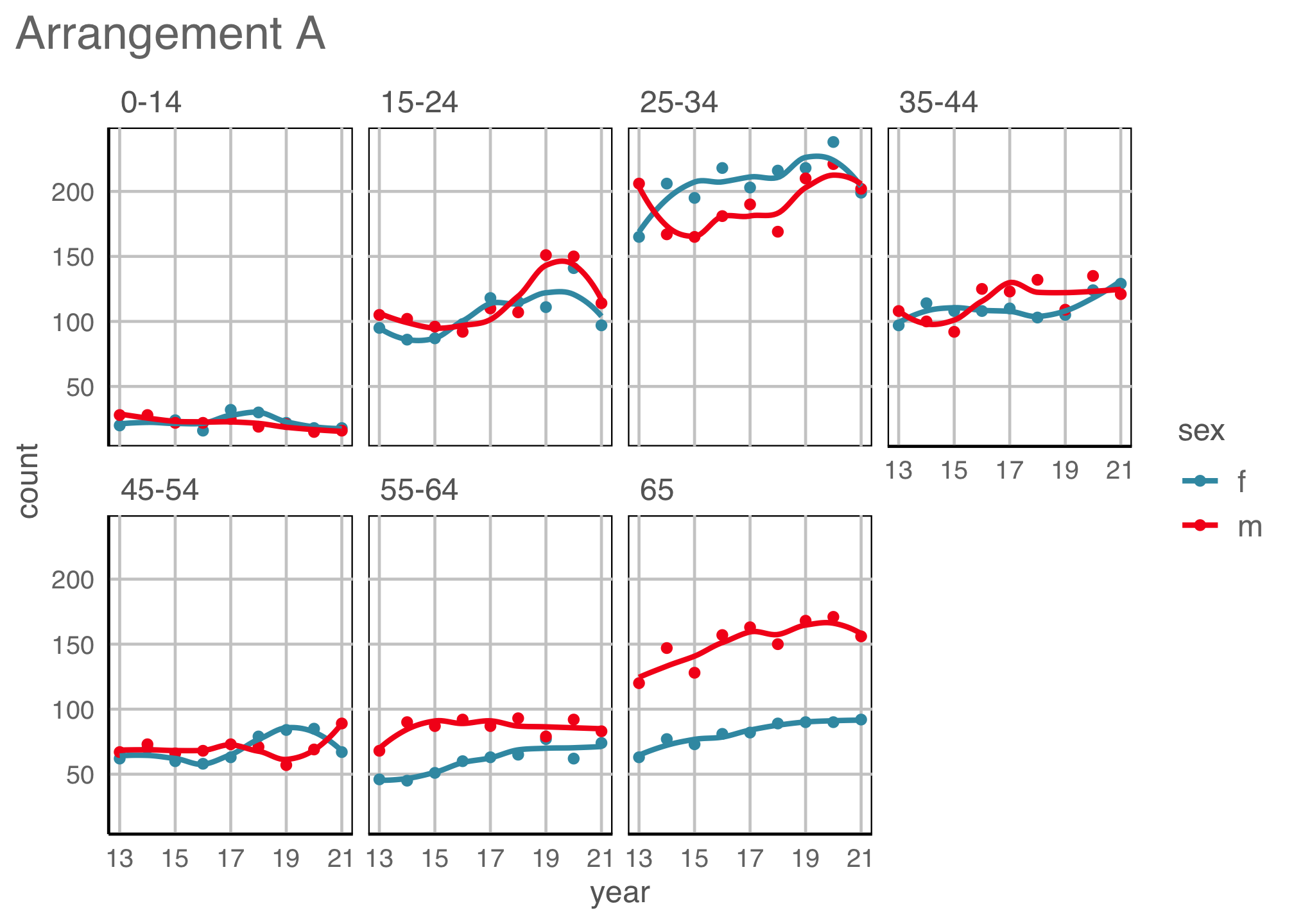
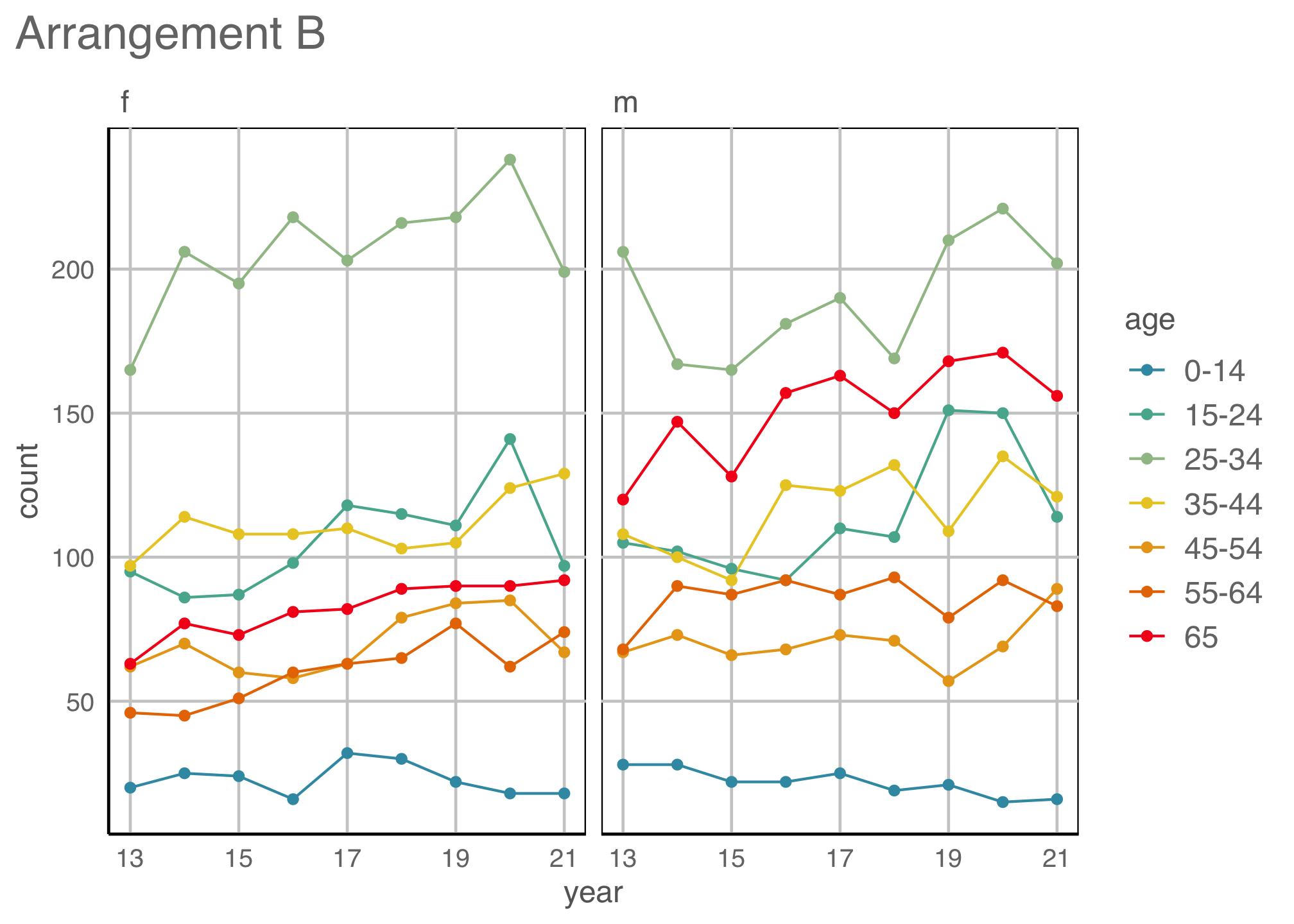
Change blindness

Making comparisons across plots requires the eye to jump from one focal point to another. It may result in not noticing differences.

Scaling

For comparison of different patterns, consider the scale. Typically the scale should be the SAME in each plot.

facet_wrap(..., scales="free_y")

Statistical thinking

Statistical thinking

• Because the plot is specified using a functional mapping of the variables, it is a statistic.
• The null and alternative hypotheses are indicated from the plot description.
• Applying the function to a dataset provides the observed value.

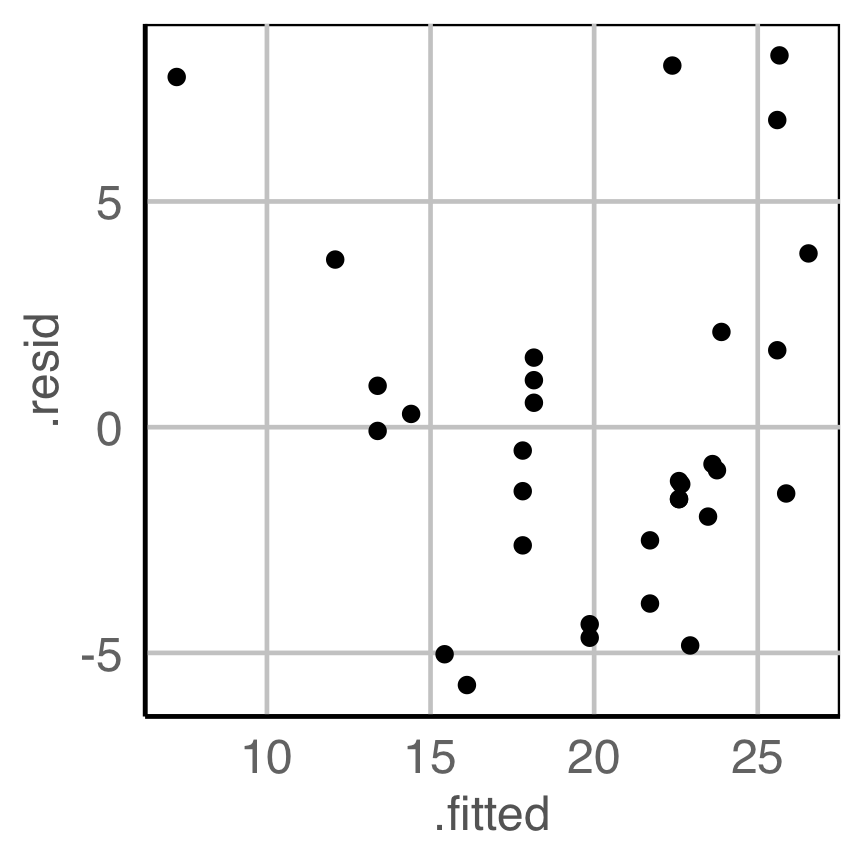
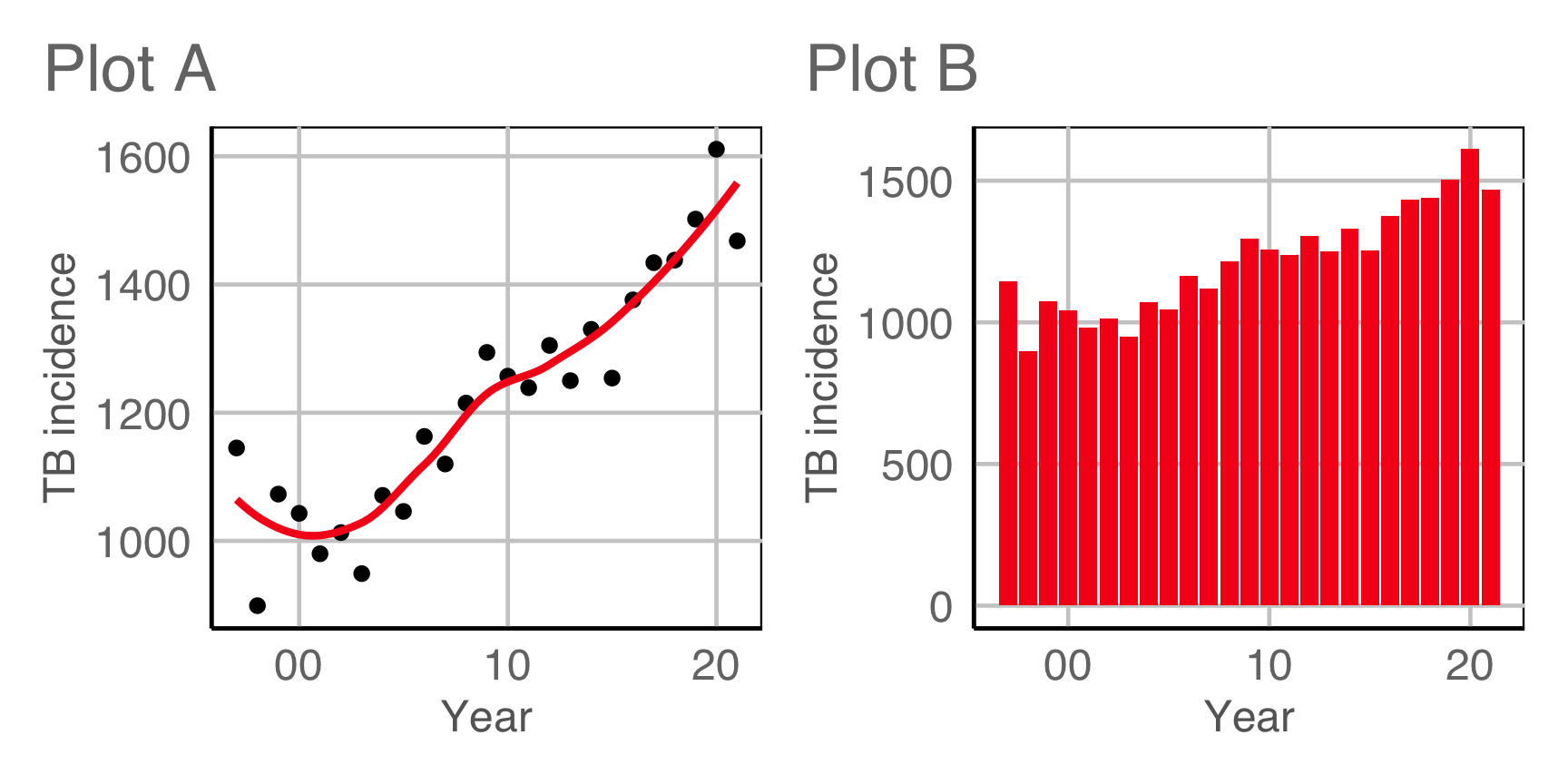
What is your plot testing? (1/3)

LM_FIT <- lm(VAR2 ~ VAR1, 
             data = DATA)
FIT_ALL <- augment(LM_FIT)
ggplot(FIT_ALL, aes(x=.FITTED, 
                    y=.RESID)) + 
  geom_point()

What will we be assessing using this plot?

Is the model misspecified?

• non-linearity
• heteroskedasticity
• outliers/anomalies
• non-normality
• fitted value distribution

What is your plot testing? (1/3)

What do you see?

✗ non-linearity
✓ heteroskedasticity
✗ outliers/anomalies
✓ non-normality
✗ fitted value distribution is uniform

Are you sure?

What is your plot testing? (2/3)

ggplot(DATA, 
       aes(x=VAR1, 
           y=VAR2, 
           color=CLASS)) + 
  geom_point() 

What will we be assessing using this plot?

Is there a difference between the groups?

• location
• shape
• outliers/anomalies

What is your plot testing? (2/3)

What do you see?

There a difference between the groups

✓ location
✗ shape
✓ outliers/anomalies

Are you sure?

What is your plot testing? (3/3)

ggplot() + 
  geom_tile(DATA, 
    aes(x=LONGITUDE, 
        y=LATITUDE, 
        fill=VAR1)) +
  geom_path(MAP, 
        aes(x=LONGITUDE, 
            y=LATITUDE,
            group=GROUP)) +
  theme_map() 

What will we be assessing using this plot?

Is there a spatial trend?

Are there any spatial anomalies?

What is your plot testing? (3/3)

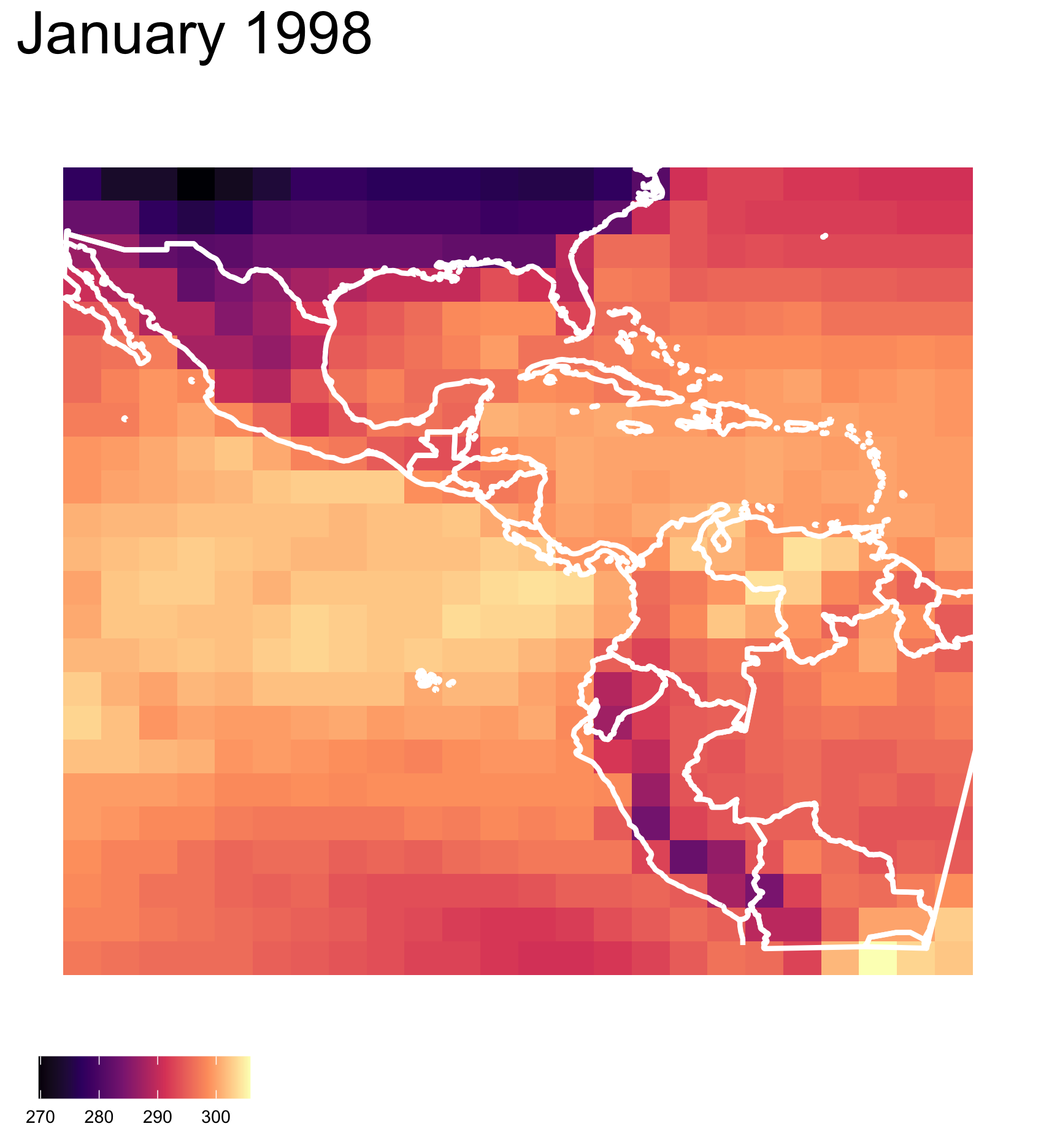
What do you see?

There are clusters of high and low temperature in different parts of the region.

✓ clusters
✓ outliers/anomalies

Are you sure?

Null hypothesis, example 1

LM_FIT <- lm(VAR2 ~ VAR1, 
             data = DATA)
FIT_ALL <- augment(LM_FIT)
ggplot(FIT_ALL, aes(x=.FITTED, 
                    y=.RESID)) + 
  geom_point()

What is the null hypothesis?

There is no relationship between residuals and fitted values. This is \(H_o\).

Alternative hypothesis, \(H_a\):

There is some relationship, which might be

• non-linearity
• heteroskedasticity
• outliers/anomalies

Null hypothesis, example 2

ggplot(DATA, 
       aes(x=VAR1, 
           y=VAR2, 
           color=CLASS)) + 
  geom_point()

What is the null hypothesis?

There is no difference between the classes. This is \(H_o\).

Alternative hypothesis, \(H_a\):

There is some difference between the classes, which might be

• location
• shape
• outliers/anomalies

Creating null samples

Creating null samples, example 1

ggplot(DATA, 
       aes(x=VAR1, 
           y=VAR2, 
           color=CLASS)) + 
  geom_point()

\(H_o\): There is no difference between the classes.

How would you generate null samples?

Break any association by permuting (scrambling/shuffling/re-sampling) the CLASS variable.

Creating null samples, example 2

LM_FIT <- lm(VAR2 ~ VAR1, 
             data = DATA)
FIT_ALL <- augment(LM_FIT)
ggplot(FIT_ALL, aes(x=.FITTED, 
                    y=.RESID)) + 
  geom_point()

\(H_o\): There is no relationship between residuals and fitted values.

How would you generate null samples?

Break any association by

• permuting residuals,
• or residual rotation,
• or simulate residuals from a normal distribution.

Conducting a lineup test

Steps

1. Create a lineup of \(m-1\) null plots + 1 data plot, where the data plot is randomly placed among nulls. Remove any distracting information, like tick labels, titles.
2. Ask uninvolved observer(s) to pick the plot that is most different. (May need to use a crowd-sourcing service.)
3. Compute the probability that the data plot was chosen, assuming it is no different from the null plots. This is the \(p\)-value.
4. Decide to reject or fail to reject the null.

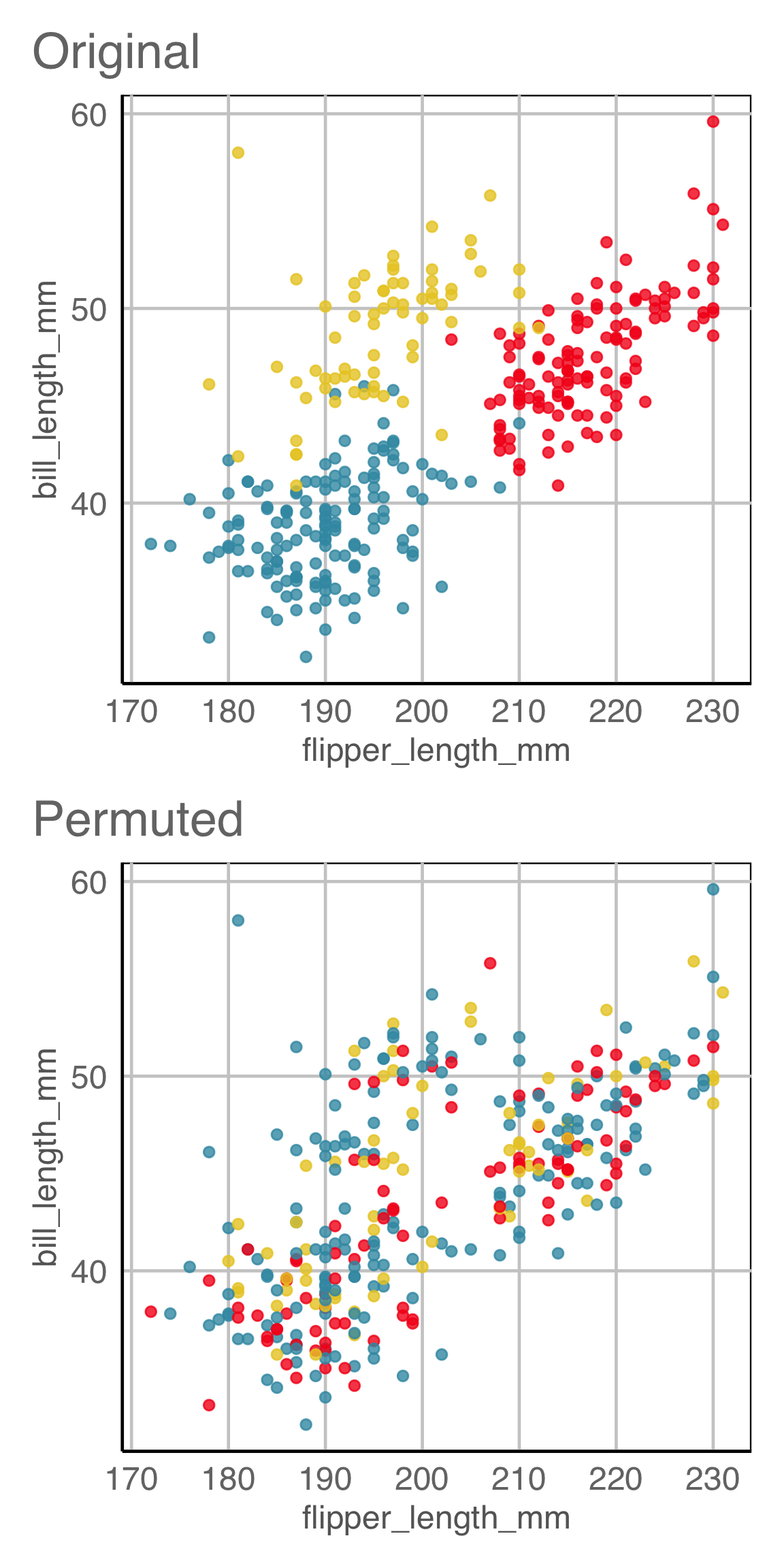
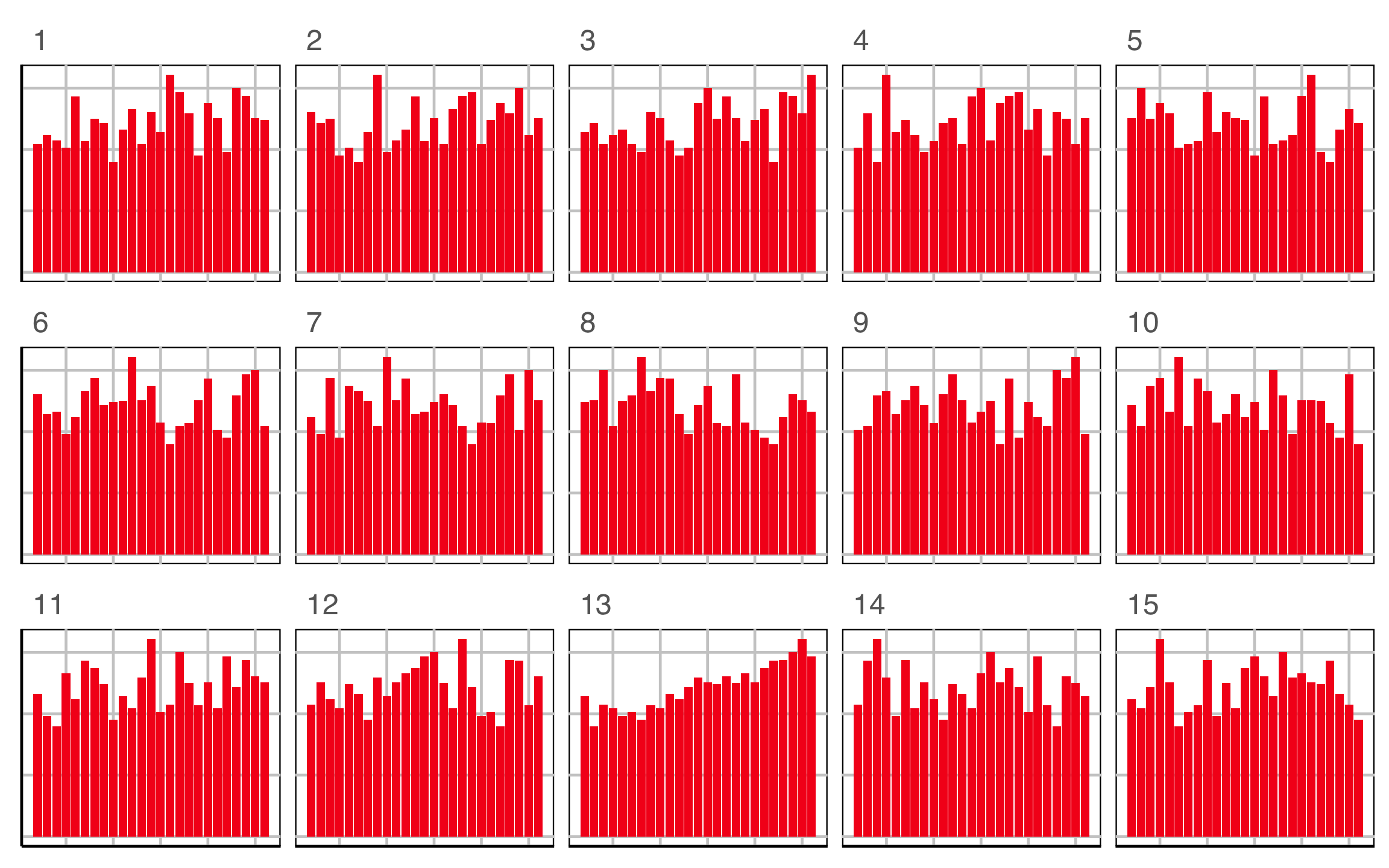
Lineup example 1 (1/2)

set.seed(241)
ggplot(lineup(null_permute("species"), penguins, n=15), 
       aes(x=flipper_length_mm, 
           y=bill_length_mm, 
           color=species)) + 
  geom_point(alpha=0.8) +
  facet_wrap(~.sample, ncol=5) +
  scale_color_discrete_divergingx(palette="Zissou 1") +
  theme(legend.position = "none",
        axis.title = element_blank(),
        axis.text = element_blank(),
        panel.grid.major = element_blank())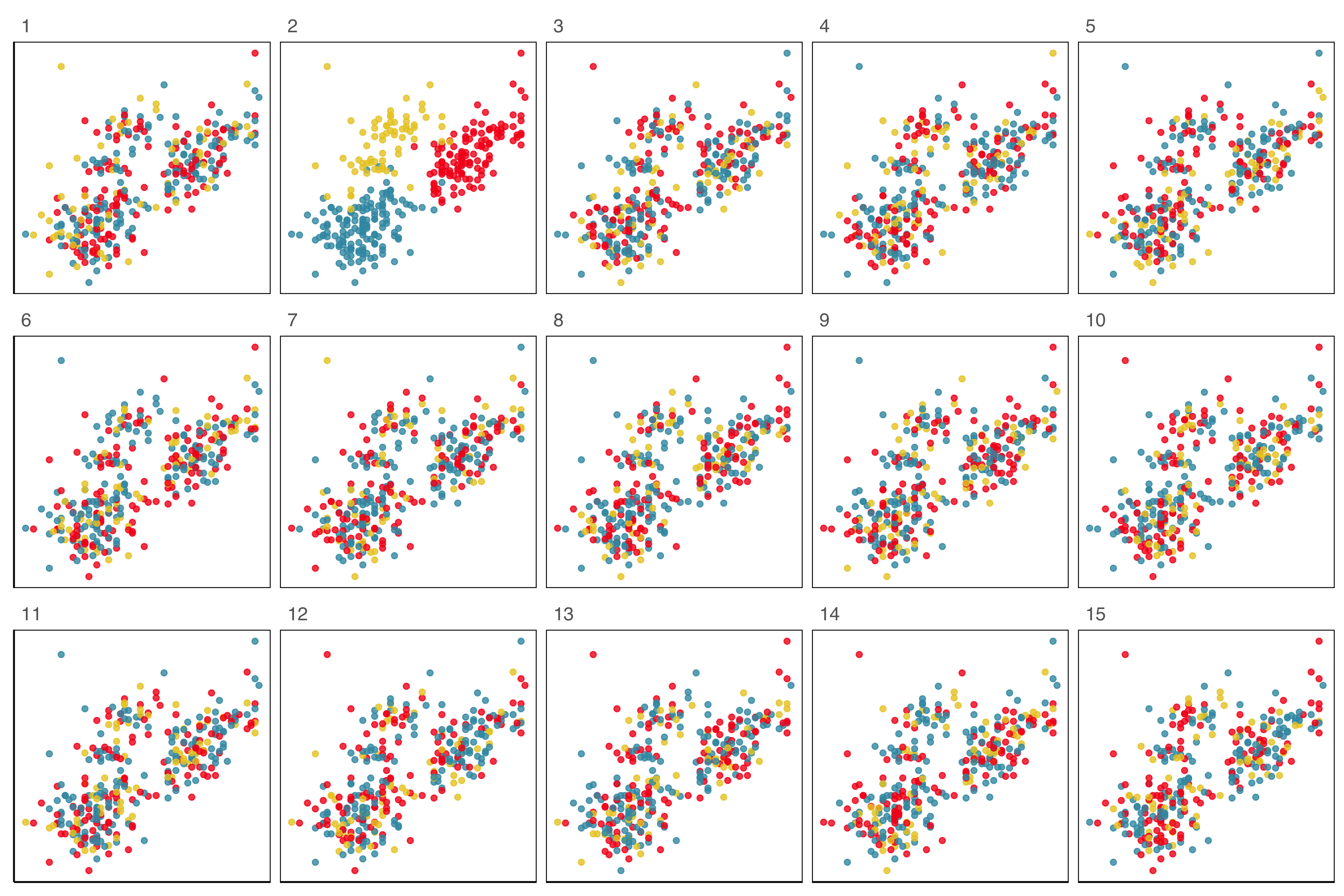

Lineup example 1 (2/2)

If 10 people are shown this lineup and all 10 pick plot 2, which is the data plot, the \(p\)-value will be 0.

Generally, we can compute the probability that the data plot is chosen by \(x\) out of \(K\) observers, shown a lineup of \(m\) plots, using a simulation approach that extends from a binomial distribution, with \(p=1/m\).

pvisual(10, 10, 15)

      x simulated        binom
[1,] 10         0 1.734168e-12

This means we would reject \(H_o\) and conclude that there is a difference in the distribution of bill length and flipper length between the species of penguins.

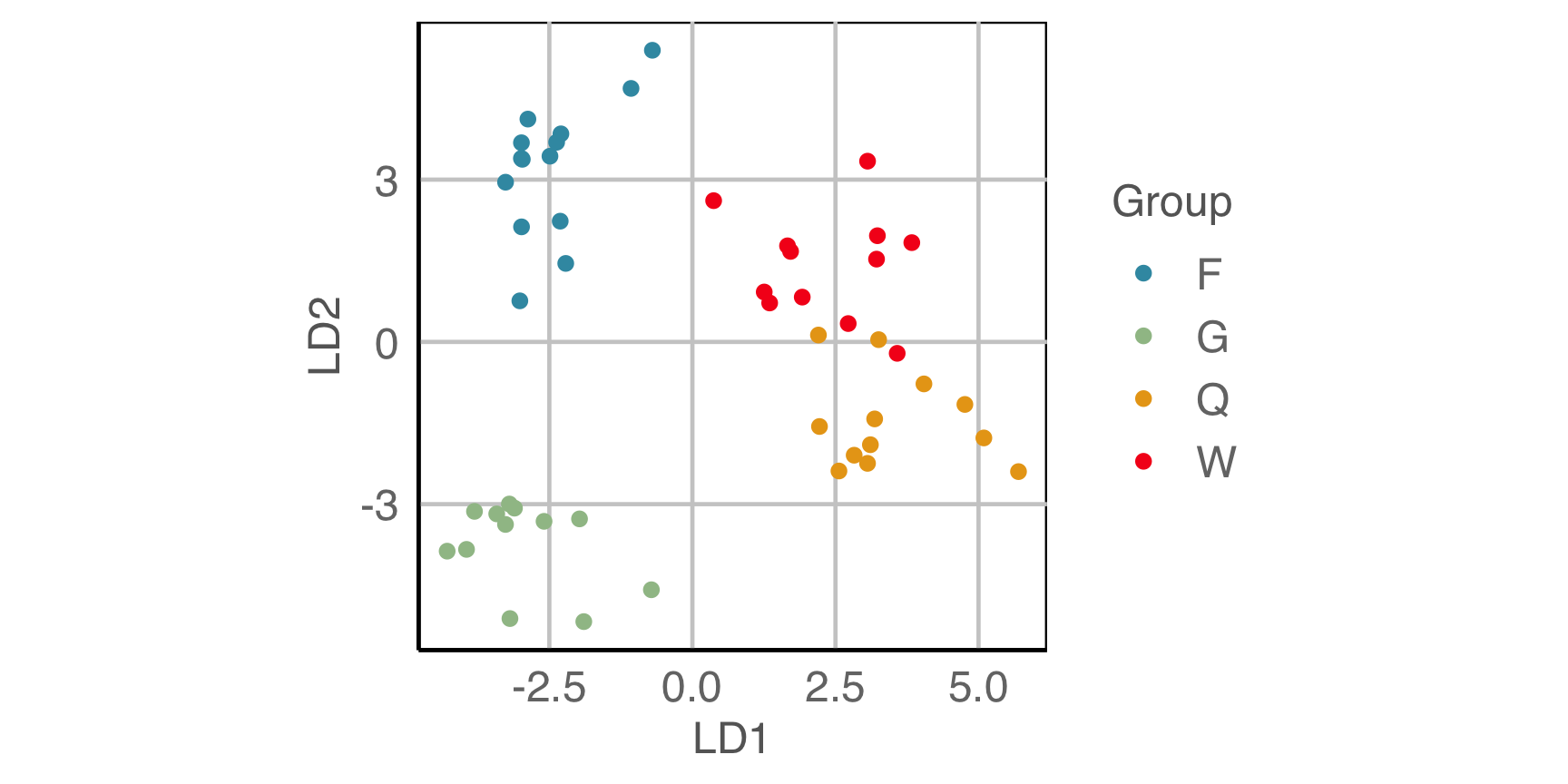
Lineup example 2 (1/2)

data(wasps)
set.seed(258)
wasps_l <- lineup(null_permute("Group"), wasps[,-1], n=15)
wasps_l <- wasps_l |>
  mutate(LD1 = NA, LD2 = NA)
for (i in unique(wasps_l$.sample)) {
  x <- filter(wasps_l, .sample == i)
  xlda <- MASS::lda(Group~., data=x[,1:42])
  xp <- MASS:::predict.lda(xlda, x, dimen=2)$x
  wasps_l$LD1[wasps_l$.sample == i] <- xp[,1]
  wasps_l$LD2[wasps_l$.sample == i] <- xp[,2]
}
ggplot(wasps_l, 
       aes(x=LD1, 
           y=LD2, 
           color=Group)) + 
  geom_point(alpha=0.8) +
  facet_wrap(~.sample, ncol=5) +
  scale_color_discrete_divergingx(palette="Zissou 1") +
  theme(legend.position = "none",
        axis.title = element_blank(),
        axis.text = element_blank(),
        panel.grid.major = element_blank())

Lineup example 2 (2/2)

If 10 people are shown this lineup and 1 picked the data plot (position 6), which is the data plot, the \(p\)-value will be large.

pvisual(1, 10, 15)

     x simulated     binom
[1,] 1    0.4639 0.4983882

This means we would NOT reject \(H_o\) and conclude that there is NO difference in the distribution of groups.

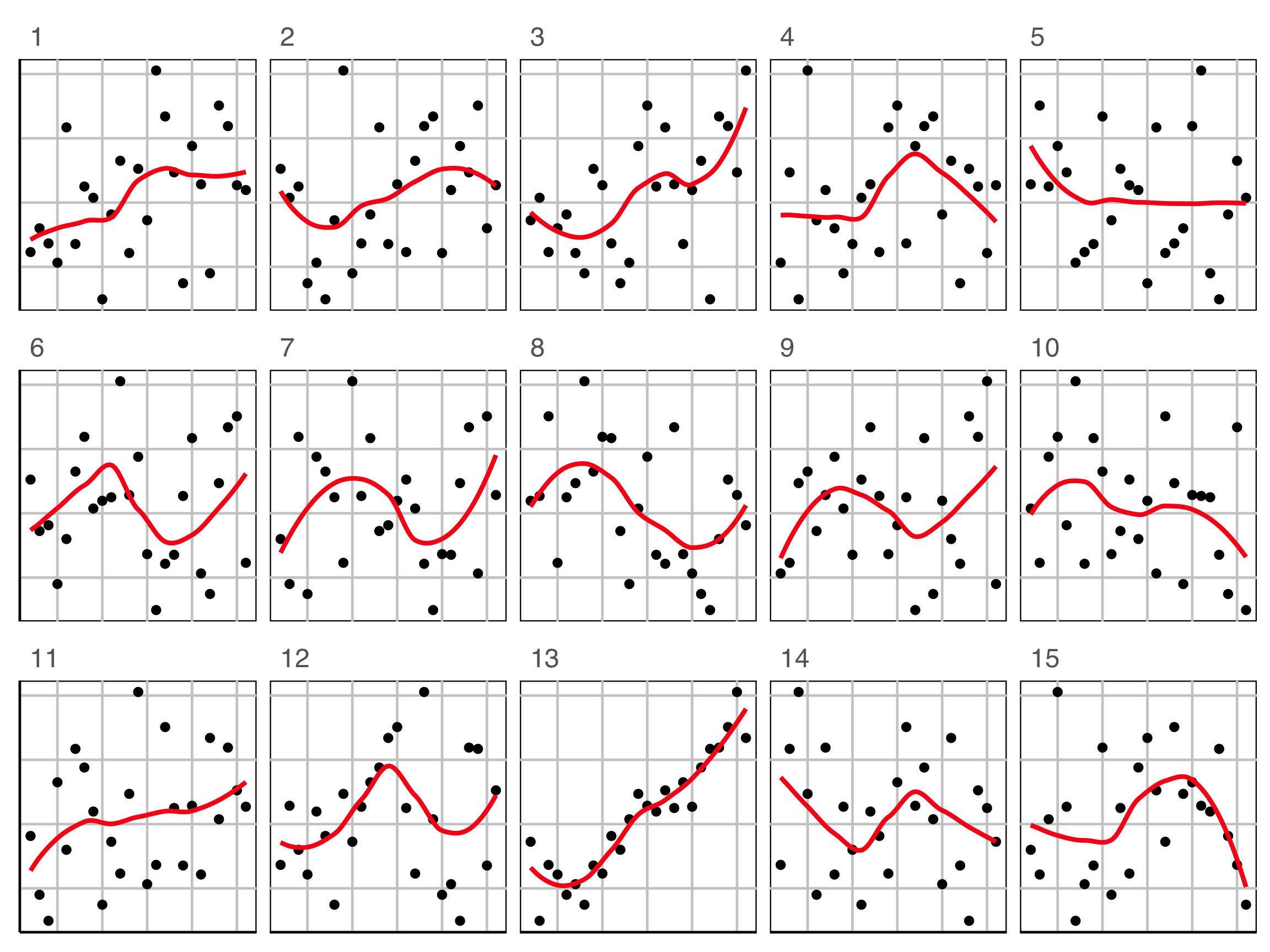
Lineup example 3 (1/2)

Which plot is the most different?

Lineup example 3 (2/2)

Plot description was:

ggplot(stars, aes(x=temp)) +
  geom_density()

In particular, the researcher is interested to know if star temperature is a skewed distribution.

\(H_o: X\sim exp(\widehat{\lambda})\)
\(H_a:\) it has a different distribution.

Generate the lineup with:

lineup(null_dist("temp", "exp", 
  list(rate = 1 / 
         mean(dslabs::stars$temp))), 
  stars, n=15)

Compute the \(p\)-value based on your responses to the lineup (previous slide).

pvisual(n=??, k=??, m=15)

Testing for best plot design

Steps

1. Decide on plot descriptions, say two possibilities.
2. Using the same data, and same null data create lineups that only differ because of the plot description.
3. Show each lineup to two samples of uninvolved observers (one observer cannot see both lineups).
4. Compute the proportion of each sample who identified the data plot, this is the signal strength or statistical power of each plot design. Also can be evaluated on time to detect the data plot.
5. The plot with the greater value (or shorter time) is the best design (for that problem).

If your birthday is between Jan 1 and Jun 30, CLOSE YOUR EYES NOW

No peeking!

Which plot is the most different?

Raise your hand when you have chosen.

00:20

• Blank
• Plot design 1A
• Plot design 1B

Plot design example 1

This is the pair of plot designs we are evaluating.

Compute signal strength:

?? / ??

If your birthday is between Jul 1 and Dec 31, CLOSE YOUR EYES NOW

No peeking!

Which plot is the most different?

Raise your hand when you have chosen.

00:20

• Blank
• Plot design 2A
• Plot design 2B

Plot design example 2

This is the pair of plot designs we are evaluating. Comparing colour palettes used for the spatial distribution of temperature.

Compute signal strength:

?? / ??

Key take-aways

• Re-arrange your data into tidy form. Conceptually, even if it’s not feasible computationally.
• Define your plots using the grammar, conceptually even if the software you use doesn’t support it.
• Utilise valuable cognitive principles: appropriate mapping, proximity and scale.
• Make null plots for comparison, the same plot description applied to null data. Null data by construction has no interesting pattern.

To learn more

• Wickham, Cook, Hofmann, Buja (2010) Graphical Inference for Infovis, IEEE TVCG, https://doi.org/10.1109/TVCG.2010.161.
• Hofmann, Follett, Majumder, Cook (2012) Graphical Tests for Power Comparison of Competing Designs, IEEE TVCG, https://doi.org/10.1109/TVCG.2012.230.
• Buja, Cook, Hofmann, Lawrence, Lee EK, Swayne, Wickham (2009) Statistical inference for exploratory data analysis and model diagnostics, https://doi.org/10.1098/rsta.2009.0120.
• Majumder, Hofmann, Cook (2013) Validation of visual statistical inference, applied to linear models, https://doi.org/10.1080/01621459.2013.808157.
• VanderPlas, Rottger, Cook, Hofmann (2021) Statistical significance calculations for scenarios in visual inference, https://doi.org/10.1002/sta4.337.

Acknowledgements

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.