Interactively Exploring Market Segmentation with High-dimensional Visualisation

Dianne Cook
Econometrics and Business Statistics
Monash University
Joint work with Ursula Laa, Matthias Medl, BOKU

You can’t see beyond 3D!

You can’t see beyond 3D!

We are going to see that we can gain intuition for structure in high dimensions through visualisation

The greatest value of a data plot is when it forces us to notice what we never expected to see. ~Adapted from a Tukey quote.

It doesn’t mean that it’s easy. It doesn’t mean that visualisation is used alone. It means that (high-dimensional) visualisation is an important part of your toolbox, especially to allow discovery of what we don’t know.

Outline

• Using a tour to see into high dimensions
• Why use a tour
• Algorithms in the tourr package
• New developments in recent years
• Using tours to understand dimension reduction and clustering
• Applying to market segmentation
• Future research directions

High-dimensional visualisation

Tours of high-dimensional data are like examining the shadows (projections)

(and slices/sections to see through a shadow)

High-dimensions in statistics

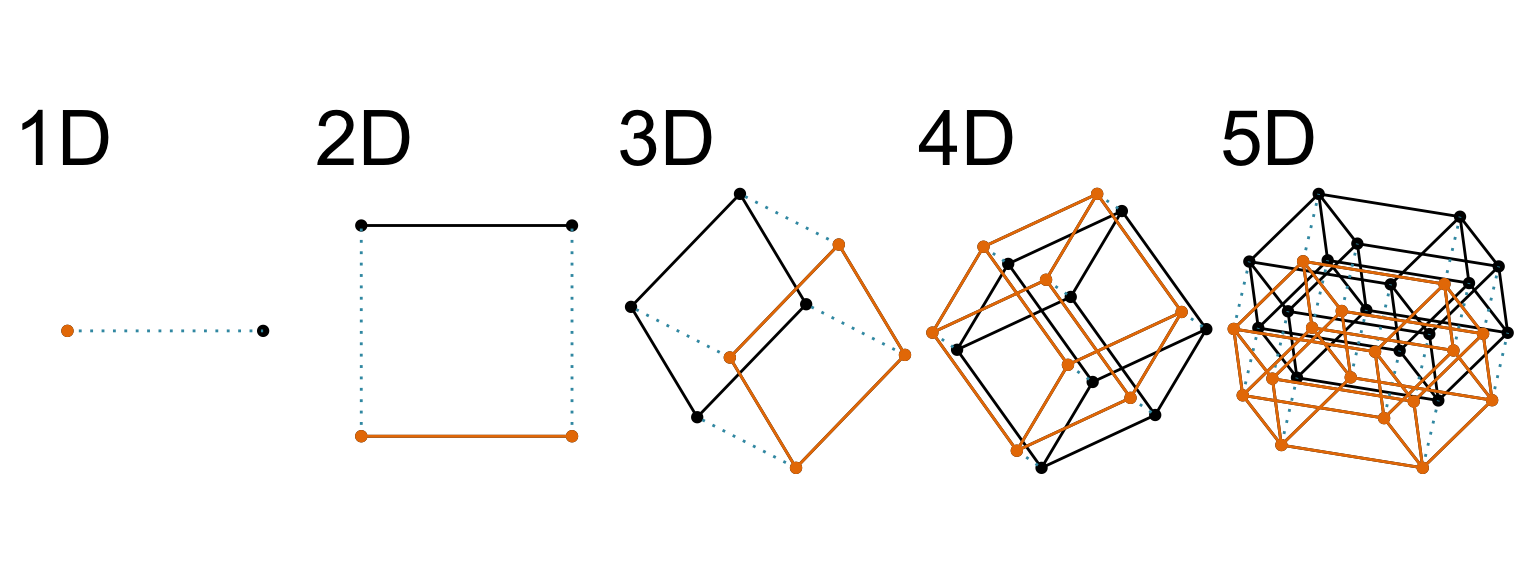
Increasing dimension adds an additional orthogonal axis.

If you want more high-dimensional shapes there is an R package, geozoo, which will generate cubes, spheres, simplices, mobius strips, torii, boy surface, klein bottles, cones, various polytopes, …

And read or watch Flatland: A Romance of Many Dimensions (1884) Edwin Abbott.

Explanation

Data

$$\begin{eqnarray*} X_{~n\times p} = [X_{~1}~X_{~2}~\dots~X_{~p}]_{~n\times p} = \left[ \begin{array}{cccc} x_{~11} & x_{~12} & \dots & x_{~1p} \\ x_{~21} & x_{~22} & \dots & x_{~2p}\\ \vdots & \vdots & & \vdots \\ x_{~n1} & x_{~n2} & \dots & x_{~np} \end{array} \right]_{~n\times p} \end{eqnarray*}$$

Explanation

Projection

$$\begin{eqnarray*} A_{~p\times d} = \left[ \begin{array}{cccc} a_{~11} & a_{~12} & \dots & a_{~1d} \\ a_{~21} & a_{~22} & \dots & a_{~2d}\\ \vdots & \vdots & & \vdots \\ a_{~p1} & a_{~p2} & \dots & a_{~pd} \end{array} \right]_{~p\times d} \end{eqnarray*}$$

Explanation

Projected data

$$\begin{eqnarray*} Y_{~n\times d} = XA = \left[ \begin{array}{cccc} y_{~11} & y_{~12} & \dots & y_{~1d} \\ y_{~21} & y_{~22} & \dots & y_{~2d}\\ \vdots & \vdots & & \vdots \\ y_{~n1} & y_{~n2} & \dots & y_{~nd} \end{array} \right]_{~n\times d} \end{eqnarray*}$$

High-dimensional visualisation

Data is 2D: $~~p=2$

Projection is 1D: $~~d=1$

$$\begin{eqnarray*} A_{~2\times 1} = \left[ \begin{array}{c} a_{~11} \\ a_{~21}\\ \end{array} \right]_{~2\times 1} \end{eqnarray*}$$

Notice that the values of $A$ change between (-1, 1). All possible values being shown during the tour.

$$\begin{eqnarray*} A = \left[ \begin{array}{c} 1 \\ 0\\ \end{array} \right] ~~~~~~~~~~~~~~~~ A = \left[ \begin{array}{c} 0.7 \\ 0.7\\ \end{array} \right] ~~~~~~~~~~~~~~~~ A = \left[ \begin{array}{c} 0.7 \\ -0.7\\ \end{array} \right] \end{eqnarray*}$$

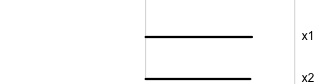
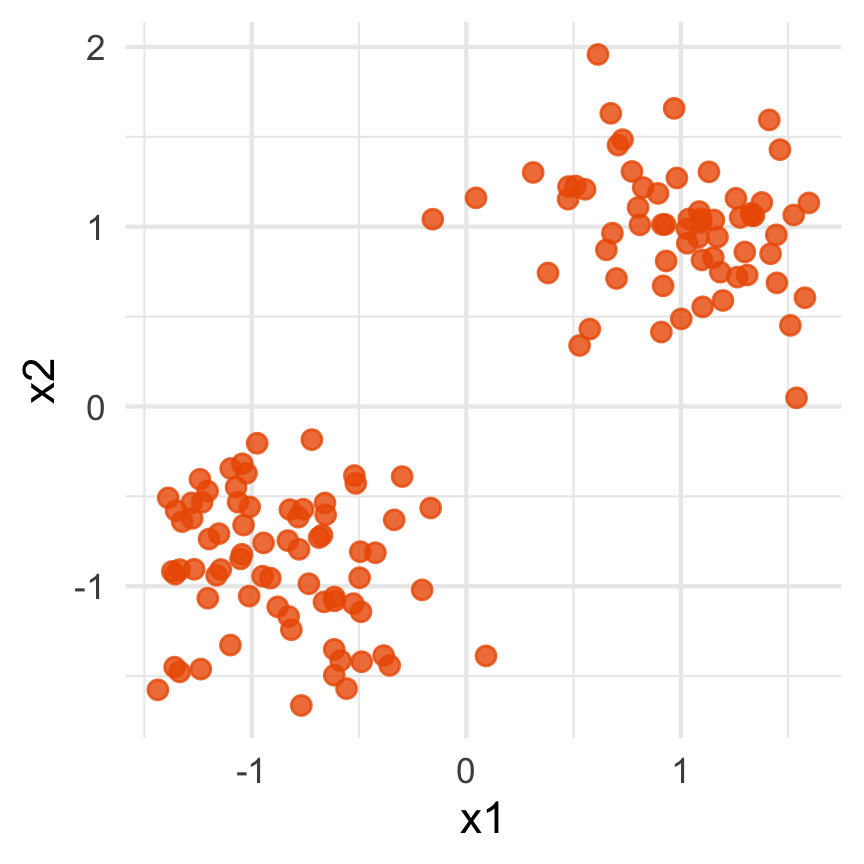
watching the 1D shadows we can see:

• unimodality
• bimodality, there are two clusters.

What does the 2D data look like? Can you sketch it?

High-dimensional visualisation

⟵
The 2D data

High-dimensional visualisation

Data is 3D: $p=3$

Projection is 2D: $d=2$

$$\begin{eqnarray*} A_{~3\times 2} = \left[ \begin{array}{cc} a_{~11} & a_{~12} \\ a_{~21} & a_{~22}\\ a_{~31} & a_{~32}\\ \end{array} \right]_{~3\times 2} \end{eqnarray*}$$

Notice that the values of $A$ change between (-1, 1). All possible values being shown during the tour.

See:

• circular shapes
• some transparency, reveals middle
• hole in in some projections
• no clustering

High-dimensional visualisation

Data is 4D: $p=4$

Projection is 2D: $d=2$

$$\begin{eqnarray*} A_{~4\times 2} = \left[ \begin{array}{cc} a_{~11} & a_{~12} \\ a_{~21} & a_{~22}\\ a_{~31} & a_{~32}\\ a_{~41} & a_{~42}\\ \end{array} \right]_{~4\times 2} \end{eqnarray*}$$

How many clusters do you see?

• three, right?
• one separated, and two very close,
• and they each have an elliptical shape.

• do you also see an outlier or two?

Early tour algorithms

1D paths in 3D space

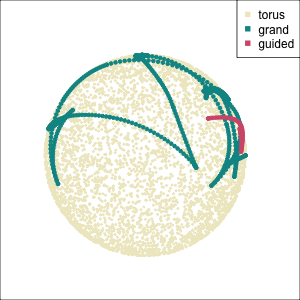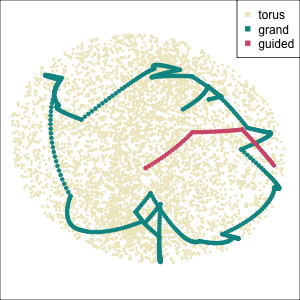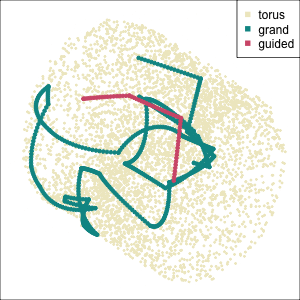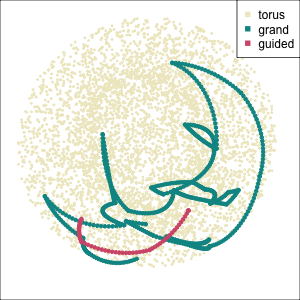
2D paths in 3D space

Early tour algorithms

Grand tour: see from all sides

Guided tour: Steer towards the most interesting features.

Why? (Three cluster data)

Avoid being a blind man inspecting the elephant

Principal component analysis

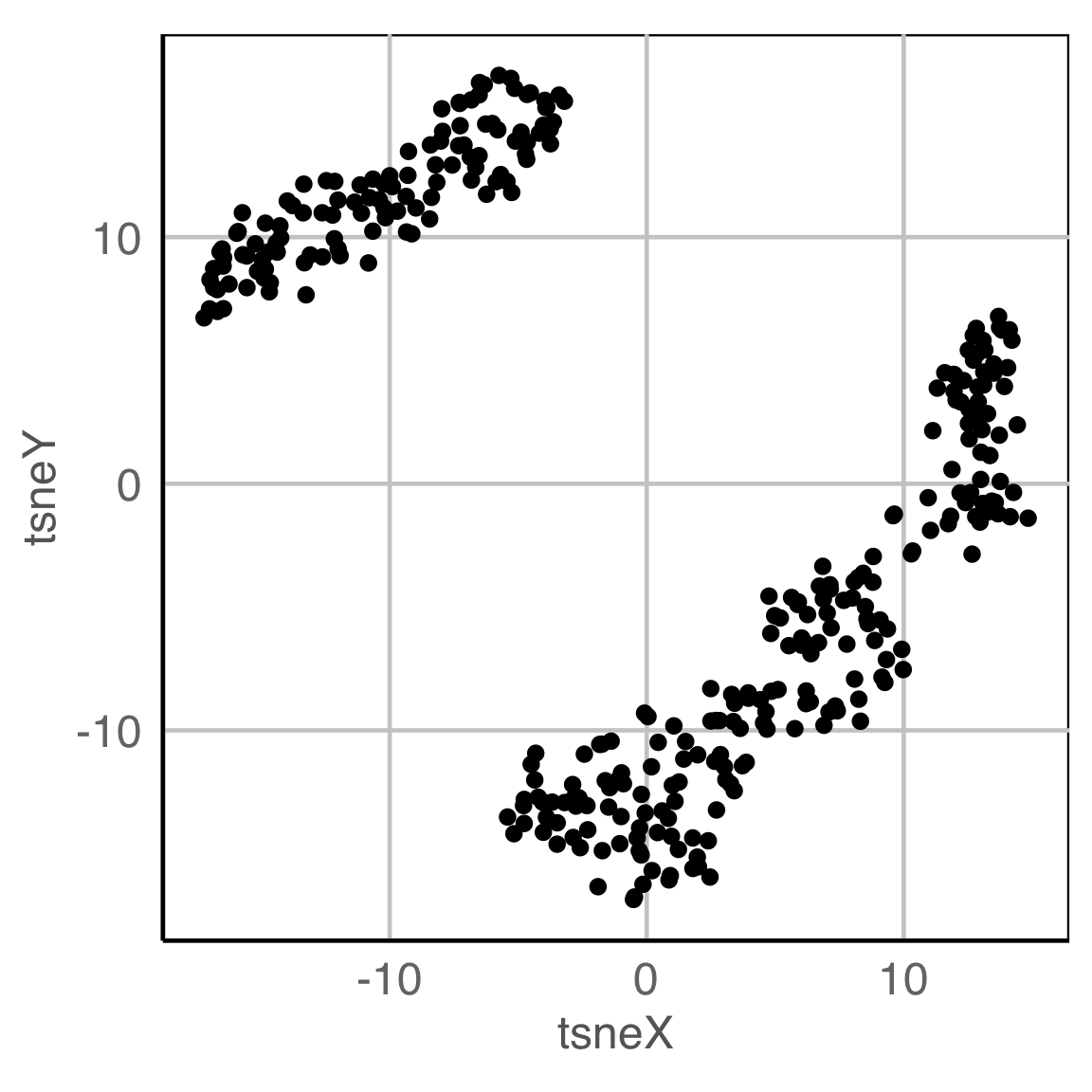
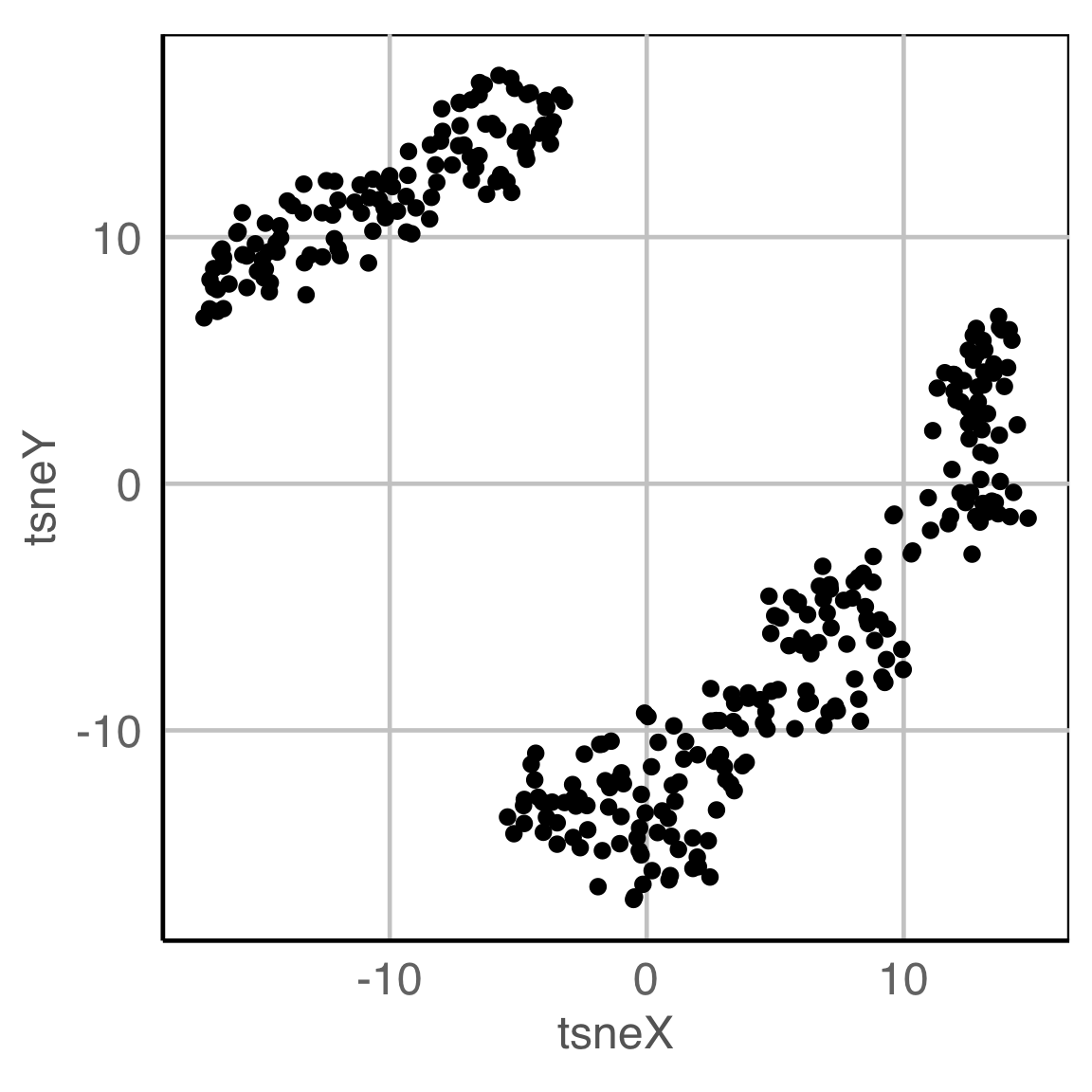
NLDR: t-Stochastic neighbourhood embedding

Philosophy: Model in the data space (1/2)

Data in the model space ¹

Model in the data space

library(mulgar)

p_pca_m <- pca_model(p_pca, s=2.2)
p_pca_m_d <- rbind(p_pca_m$points, penguins_sub[,1:4])
animate_xy(p_pca_m_d, edges=p_pca_m$edges,
           axes="bottomleft",
           edges.col="#E7950F",
           edges.width=3)
render_gif(p_pca_m_d, 
           grand_tour(), 
           display_xy(half_range=4.2,
                      edges=p_pca_m$edges, 
                      edges.col="#E7950F",
                      edges.width=3),
           gif_file="gifs/p_pca_model.gif",
           frames=500,
           width=400,
           height=400,
           loop=FALSE)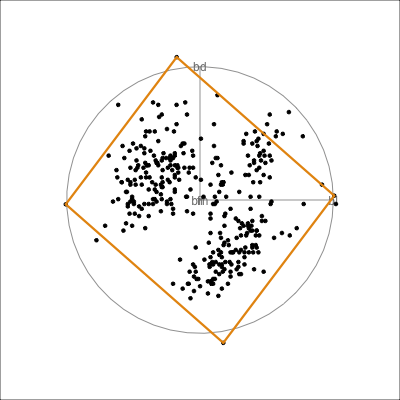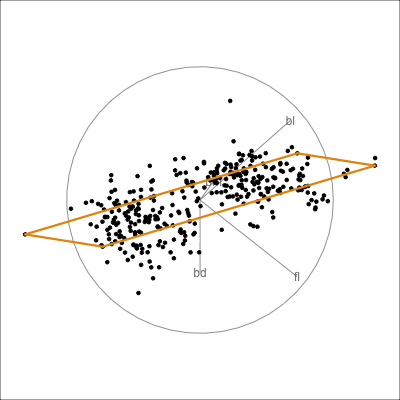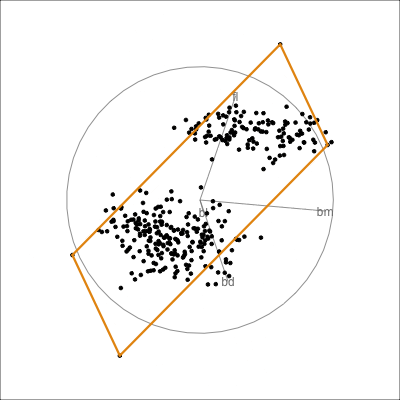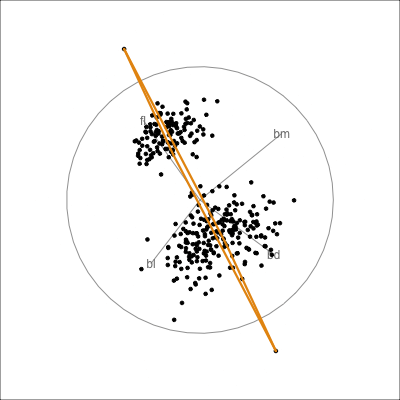

1. Wickham et al (2015) https://doi.org/10.1002/sam.11271

Philosophy: Model in the data space (2/2)

Data in the model space

Model in the data space

???

Stay tuned for new work to appear next year

Hiding in high-d (1/2)

library(tidyverse)
library(tourr)
library(GGally)
set.seed(946)
d <- tibble(x1=runif(200, -1, 1), 
            x2=runif(200, -1, 1), 
            x3=runif(200, -1, 1))
d <- d %>%
  mutate(x4 = x3 + runif(200, -0.1, 0.1))
d <- bind_rows(d, c(x1=0, x2=0, x3=-0.5, x4=0.5))

d_r <- d %>%
  mutate(x1 = cos(pi/6)*x1 + sin(pi/6)*x3,
         x3 = -sin(pi/6)*x1 + cos(pi/6)*x3,
         x2 = cos(pi/6)*x2 + sin(pi/6)*x4,
         x4 = -sin(pi/6)*x2 + cos(pi/6)*x4)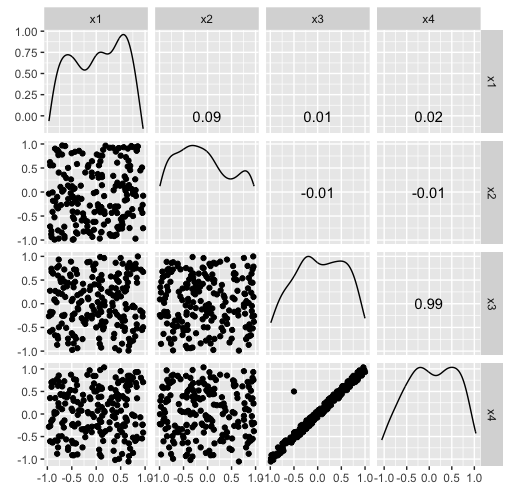

Hiding in high-d (2/2)

library(tidyverse)
library(tourr)
library(GGally)
set.seed(946)
d <- tibble(x1=runif(200, -1, 1), 
            x2=runif(200, -1, 1), 
            x3=runif(200, -1, 1))
d <- d %>%
  mutate(x4 = x3 + runif(200, -0.1, 0.1))
d <- bind_rows(d, c(x1=0, x2=0, x3=-0.5, x4=0.5))

d_r <- d %>%
  mutate(x1 = cos(pi/6)*x1 + sin(pi/6)*x3,
         x3 = -sin(pi/6)*x1 + cos(pi/6)*x3,
         x2 = cos(pi/6)*x2 + sin(pi/6)*x4,
         x4 = -sin(pi/6)*x2 + cos(pi/6)*x4)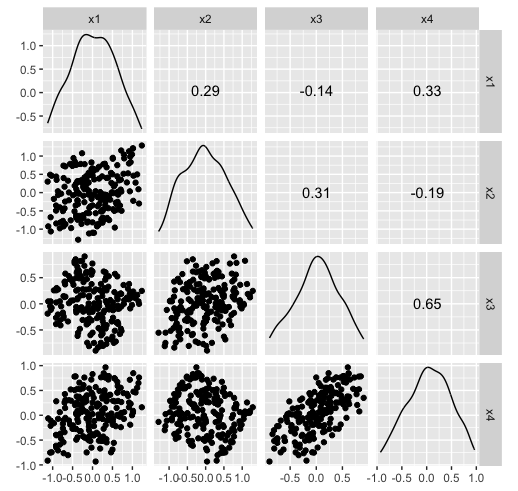

Algorithms in the tourr package

Movement

• choice of target planes
  • grand: random
  • guided: objective function
  • local: nearby
  • little: marginals
  • manual/radial: specific variable
• interpolation between them
  • geodesic: plane to plane
  • Givens: frame/basis to frame/basis

Display

How should you plot your projected data?

• 1D: density, dotplot, histogram
• 2D: scatterplot, density2D, sage, pca, slice
• 3D: stereo
• kD: parallel coordinates, scatterplot matrix
• 1D+spatial: image

The packages detourr, liminal and lionfish take the path produced by tourr functions.

Recent developments

• interactivity: detourr, liminal, langevitour, lionfish
• slice/section: explore shape of models
• manual/radial tour: explore sensitivity of structure to particular variables
• sage: correct for piling
• Givens interpolation: frame to frame

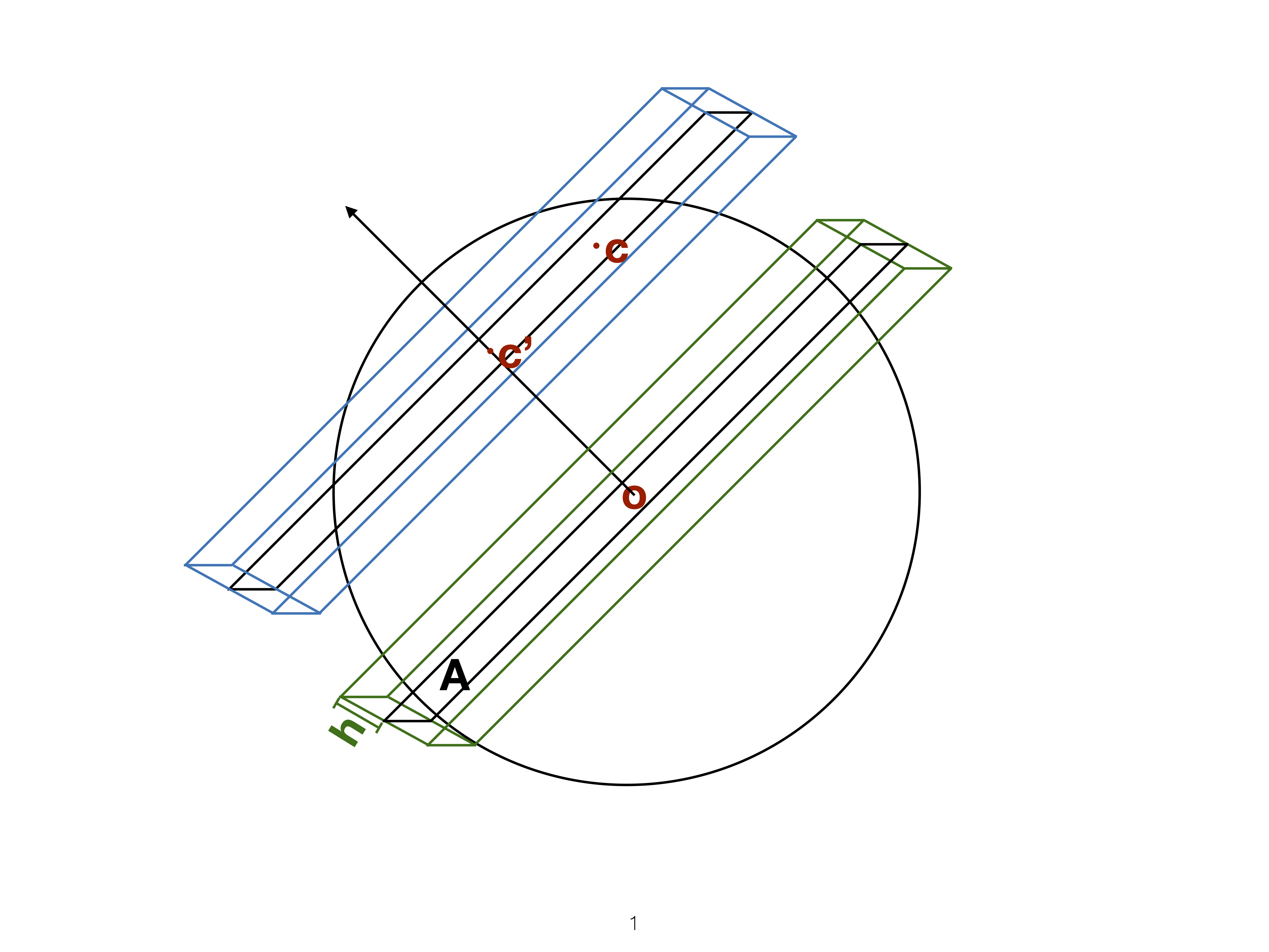
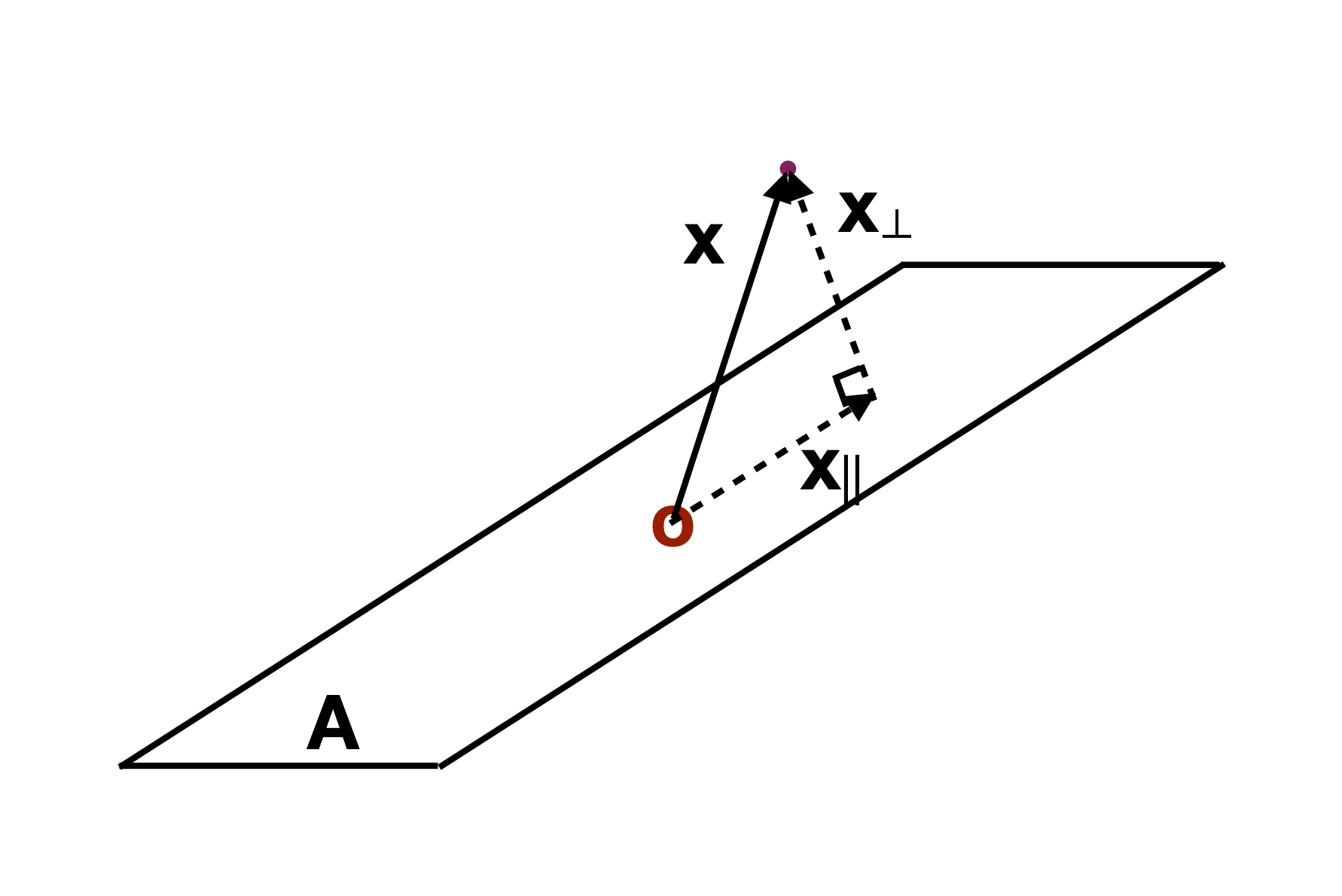
Slice

Utilise distance from the projection plane to make the slice, and shift centre of projection plane.

Sage transformation (1/2)

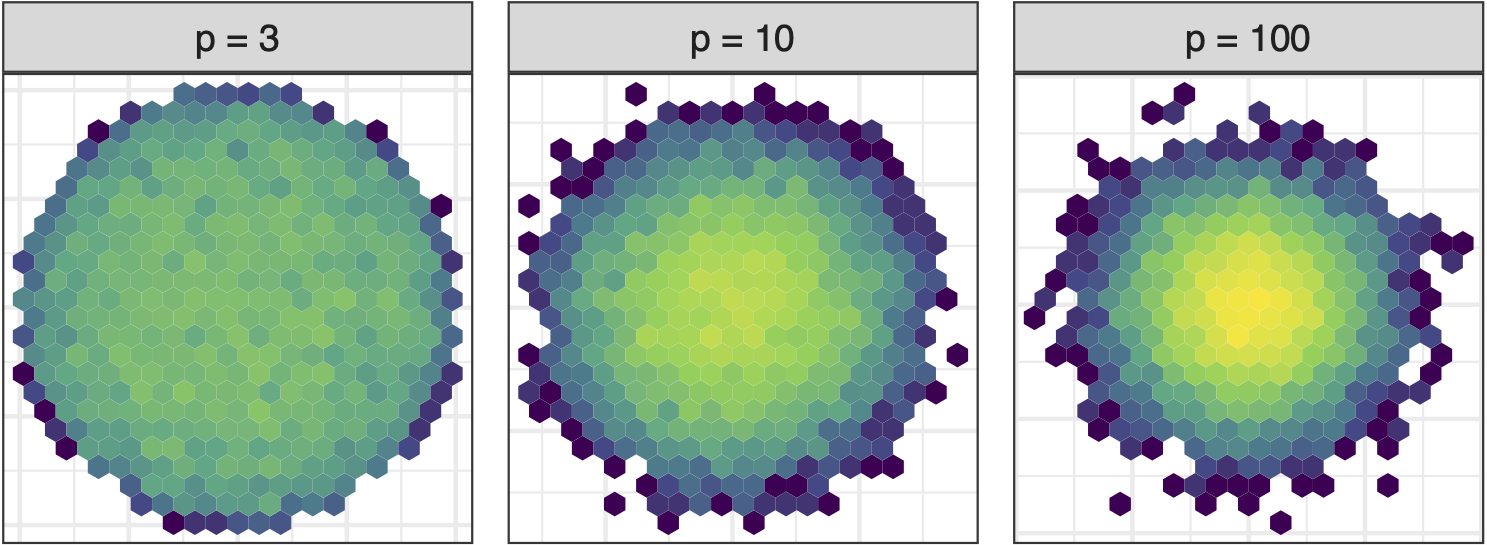
Increase variables, increase concentration, possibly obscuring important structure.

Sage transformation (2/2)

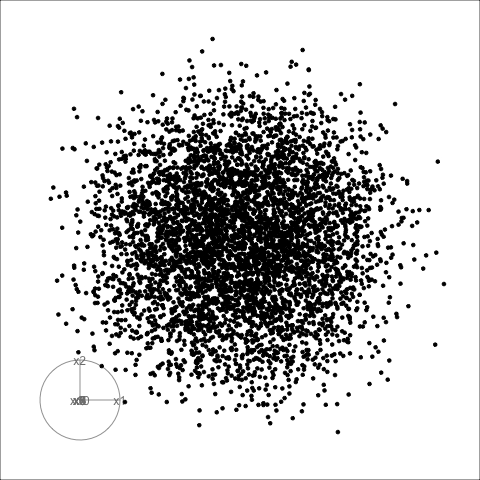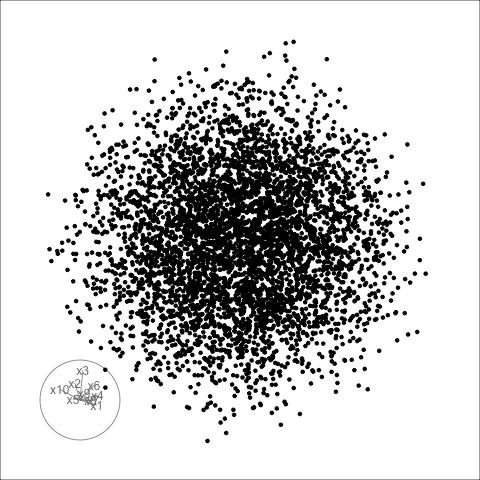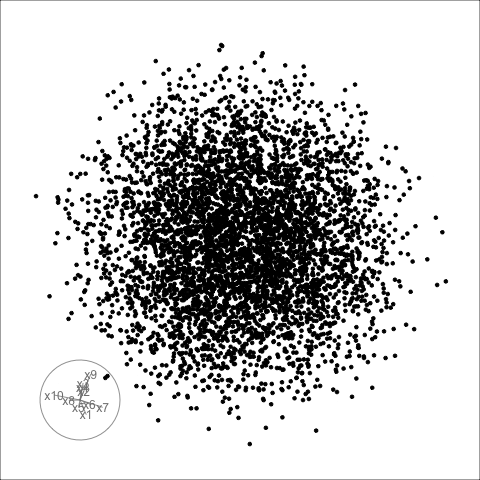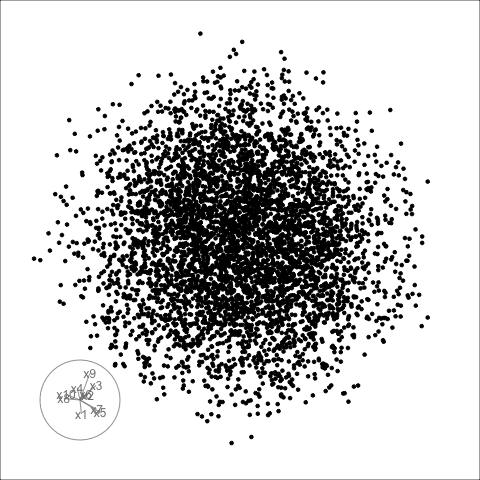
Transformation expands the centre to make a sage display.

Givens (1/2)

TARGET BASIS (would show dog if we could find)

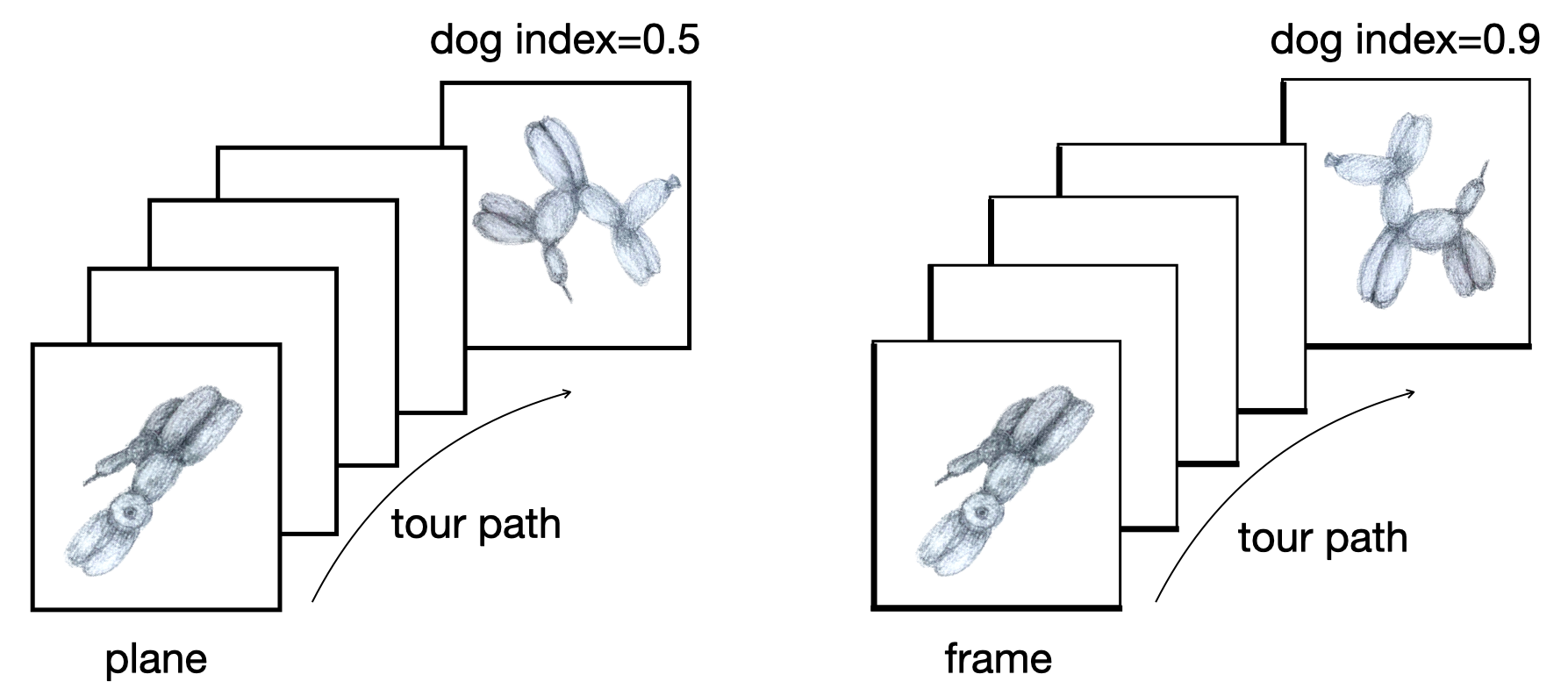
Givens (2/2)

——–Givens—–geodesic

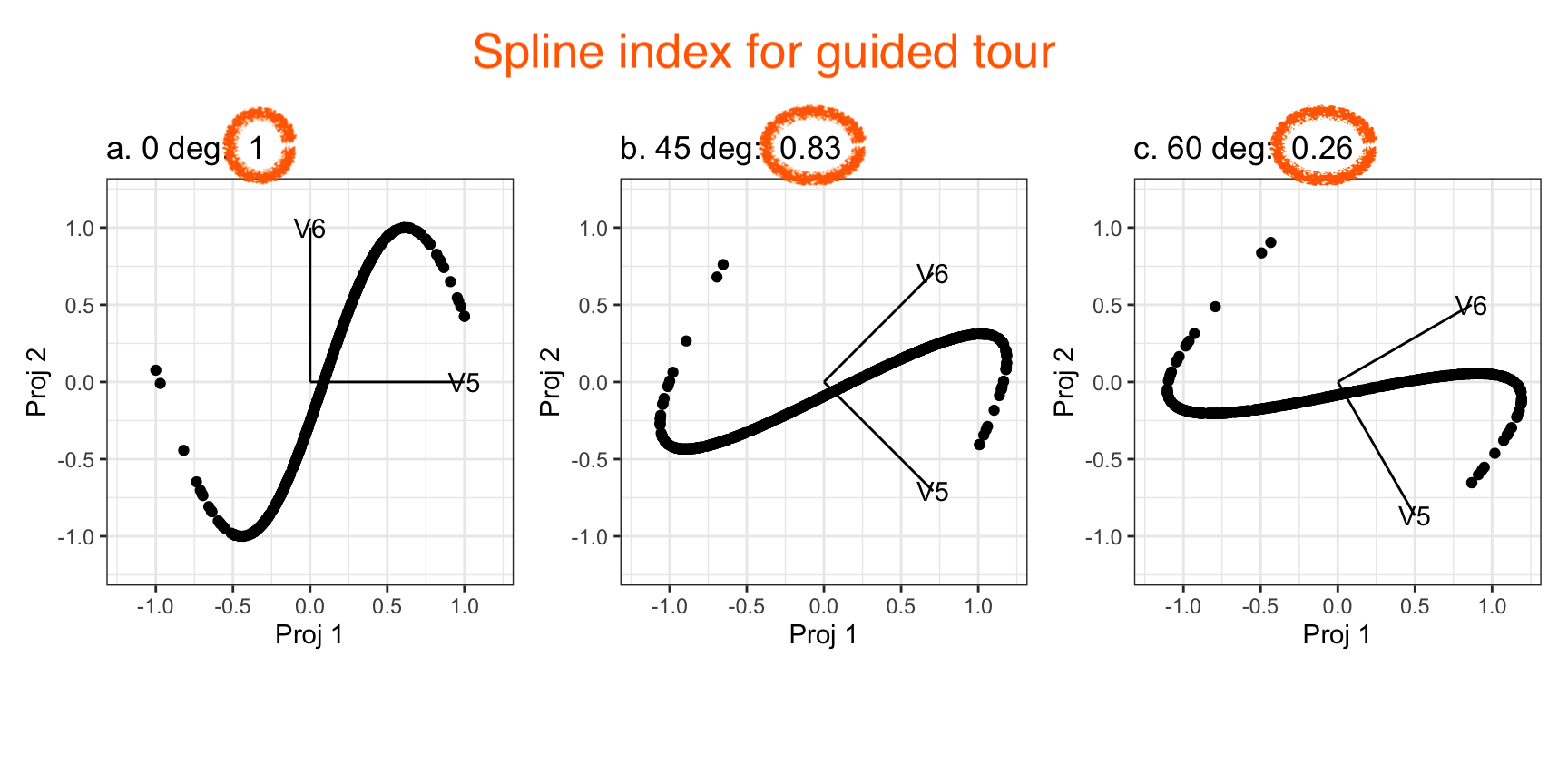
Givens interpolation ends at requested frame, but geodesic interpolation arrives at the plane, is frame-agnostic, and that is problematic for optimisation using the guided tour.

Interactivity: exploration

If you want to discover and mark the clusters you see, you can use the detourr package to spin and brush points. Here’s a live demo. Hopefully this works.

library(detourr)
set.seed(645)
detour(penguins_sub[,1:4], 
       tour_aes(projection = bl:bm)) |>
       tour_path(grand_tour(2), fps = 60, 
                 max_bases=40) |>
       show_scatter(alpha = 0.7, 
                    axes = FALSE, 
                    size = 2)

DEMO

Manual/radial tour

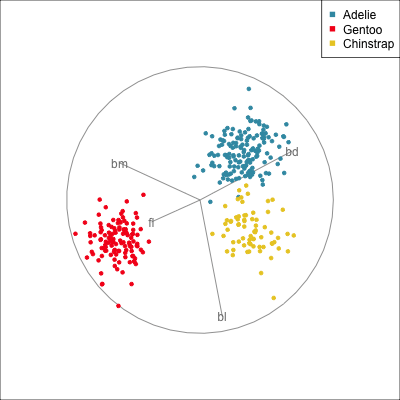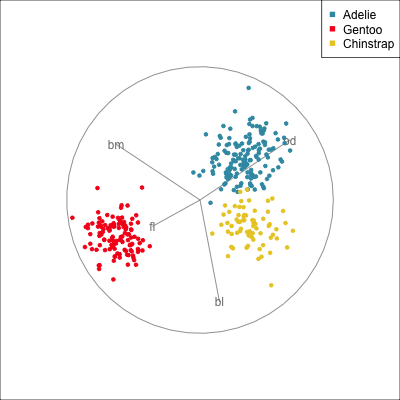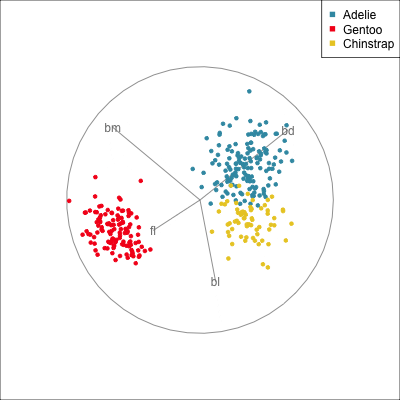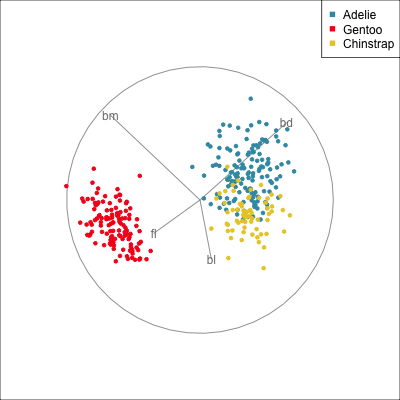
Best projection provided by the guided tour, separating three species.

Removing flipper length

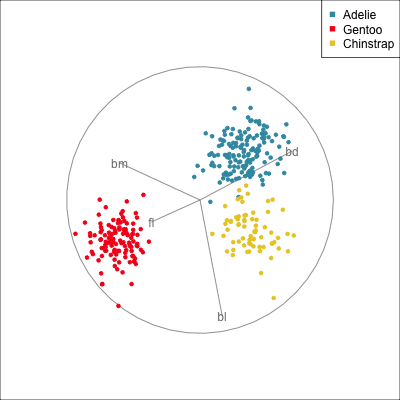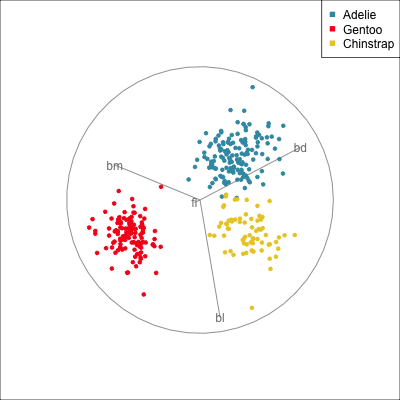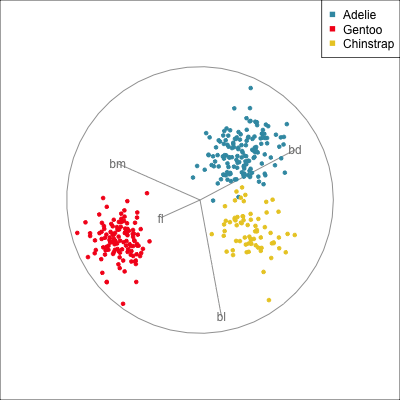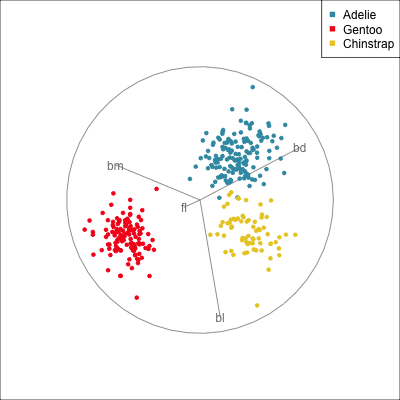
Removing bill length

Slice tour (1/2)

Projection

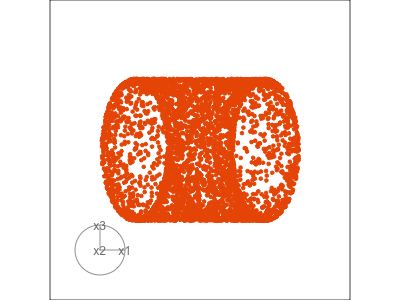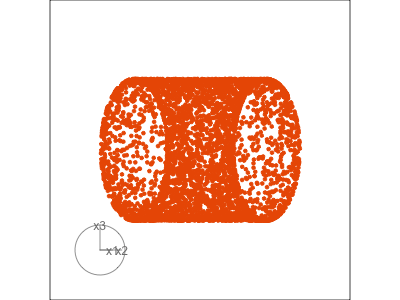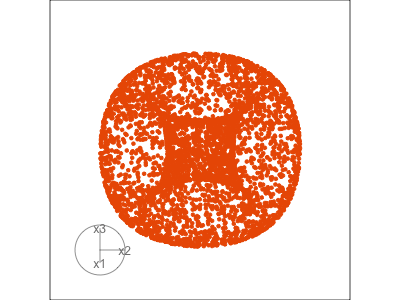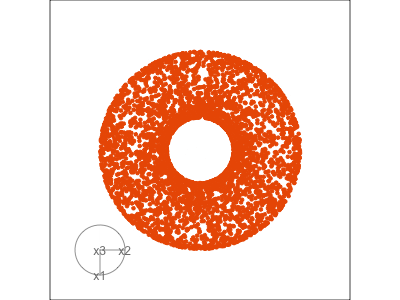
Slice

Slice tour (2/2)

This is especially useful for exploring classification models, comparing boundaries produced by different models. (The same penguins data used here.)

Linear discriminant analysis

Classification tree

Clustering & tours

Model-based - 2D (1/3)

Table of model types

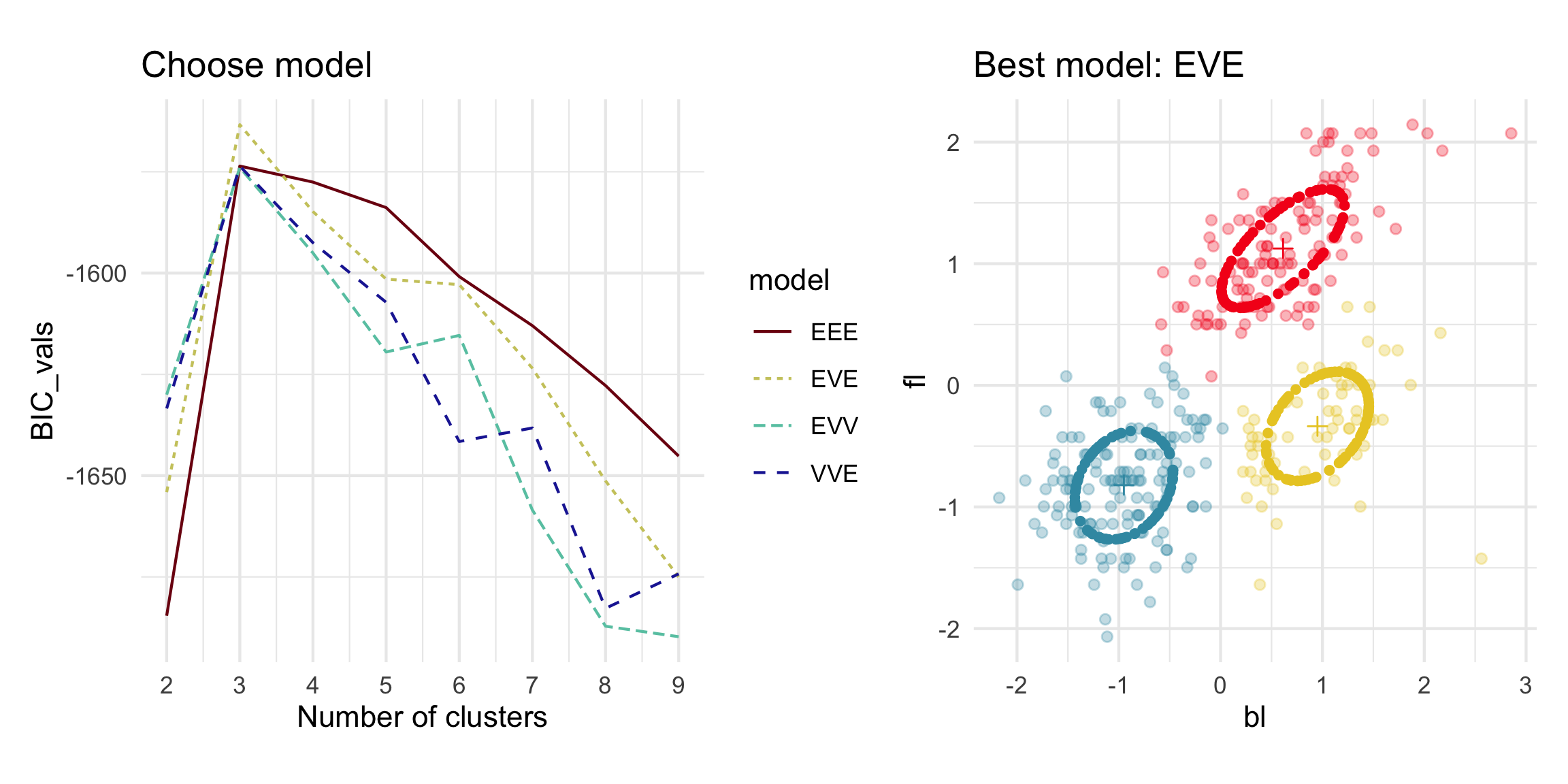
Model-based - 4D (2/3)

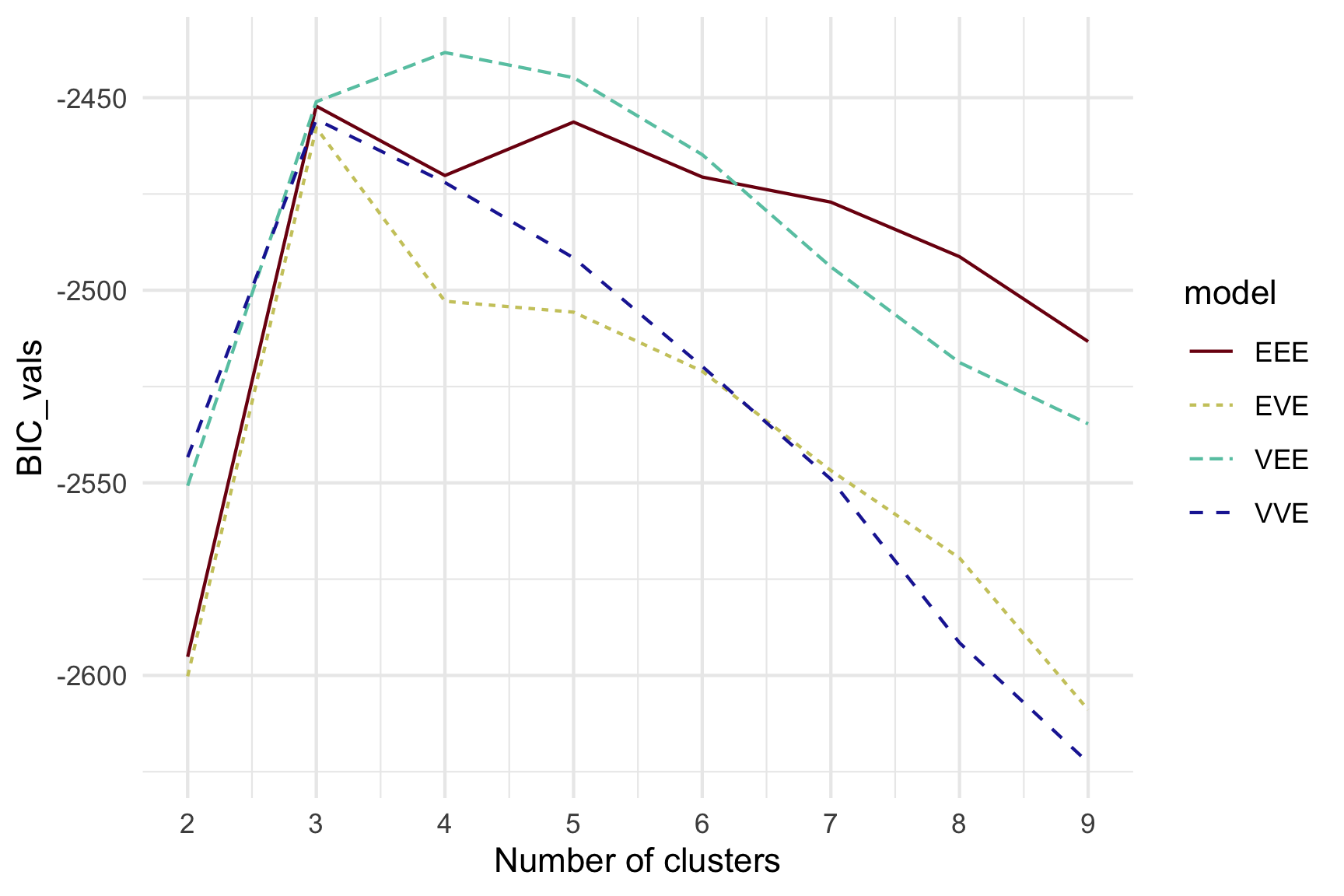
Model-based (3/3) ~~Which fits the data better?

Best model: four-cluster VEE

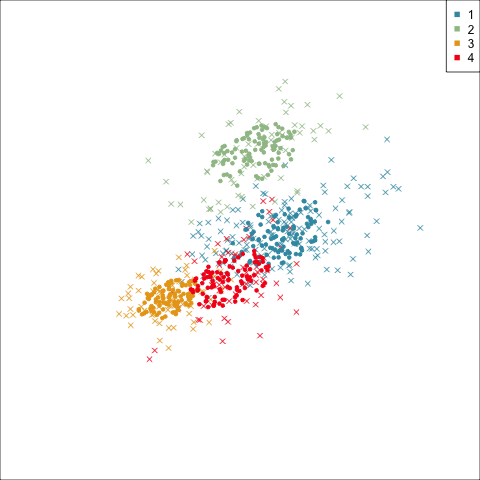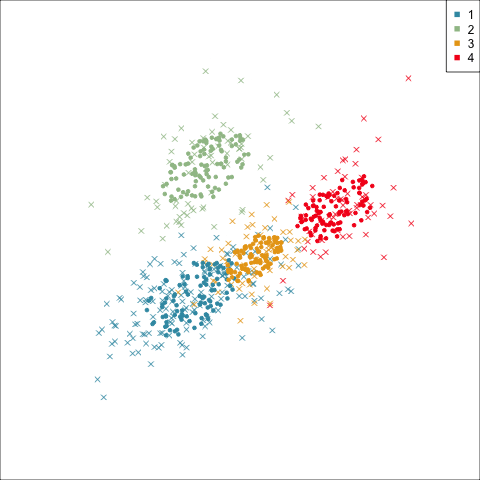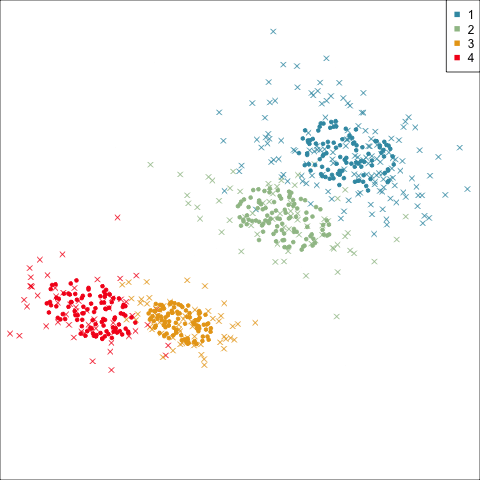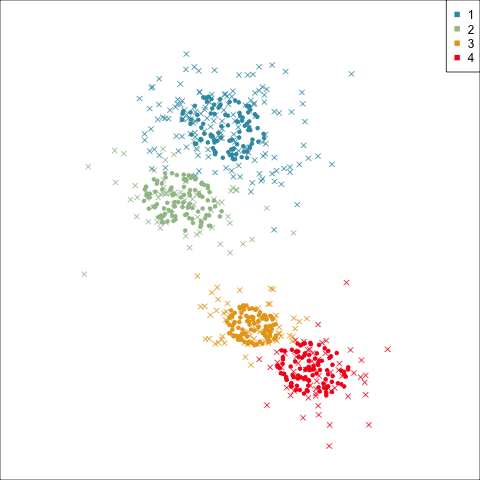
Three-cluster EEE

Table of model types

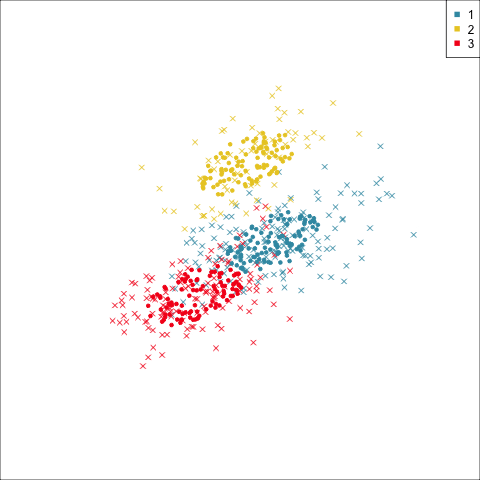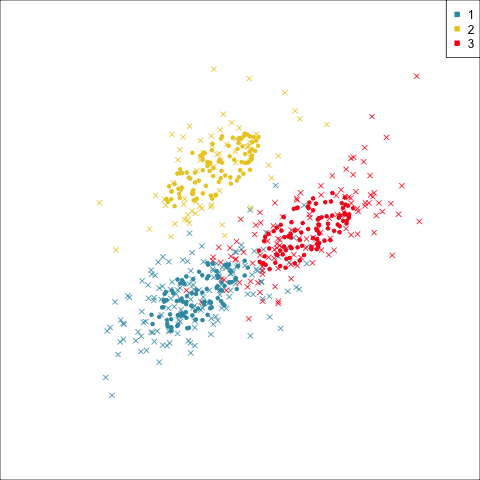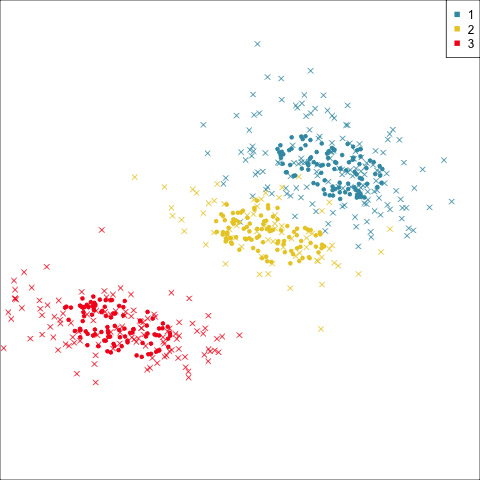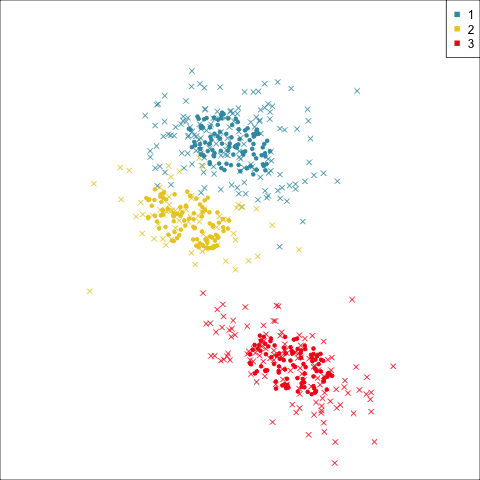
Summarising clusters

Convex hulls are often used to summarise clusters in 2D. It is possible to view these in high-d, too.

Ward’s linkage hierarchical clustering

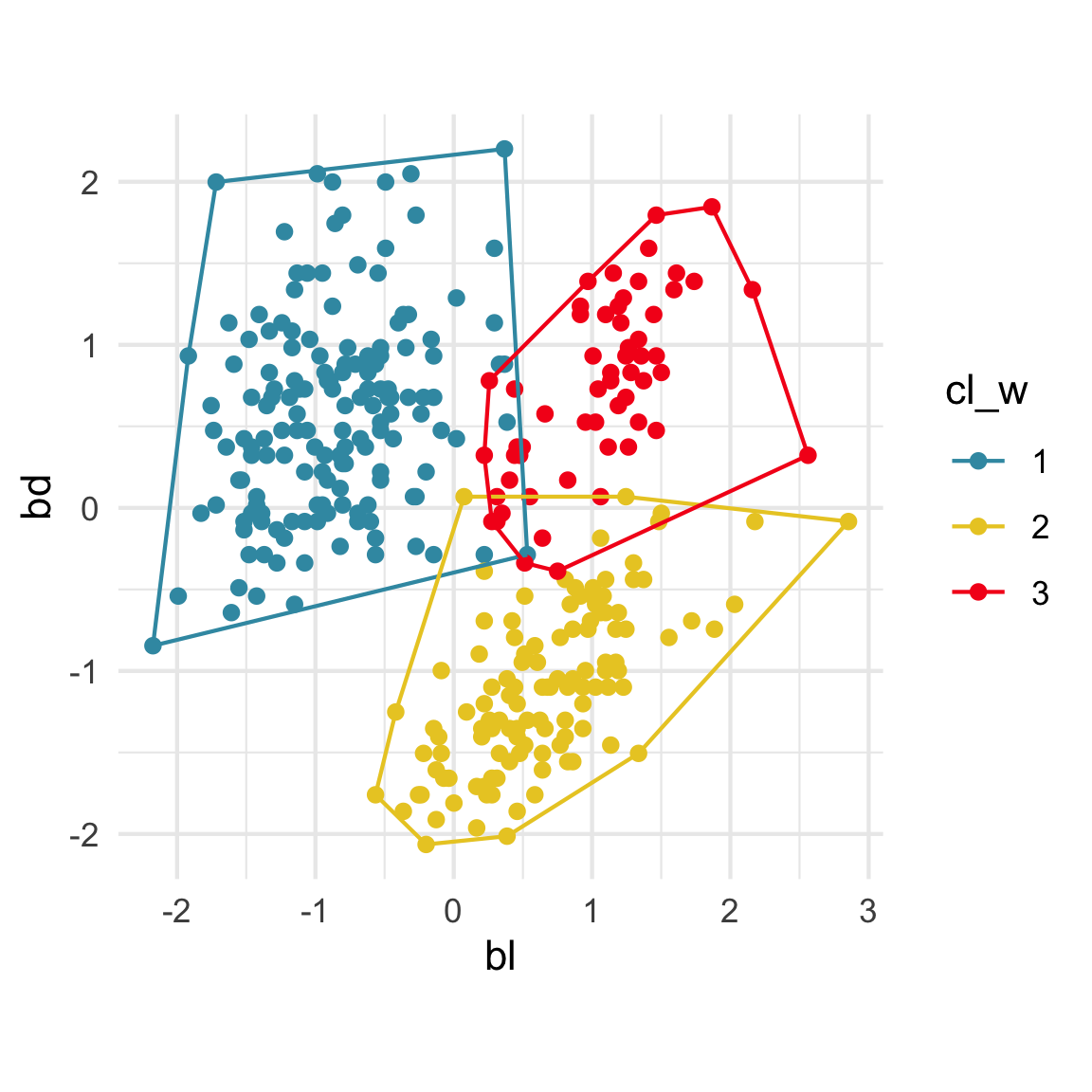
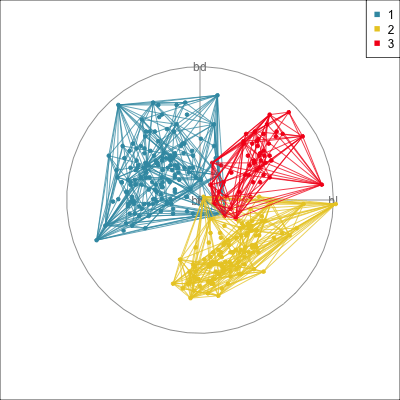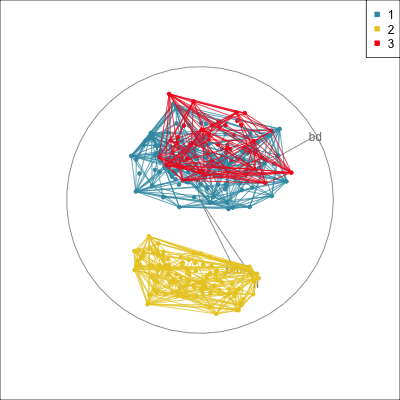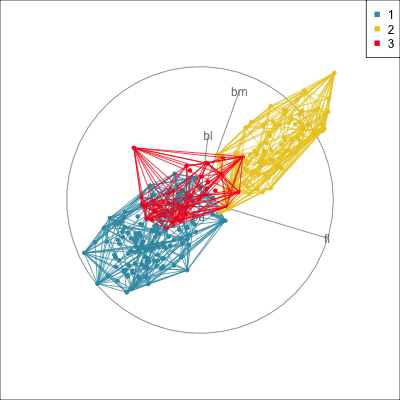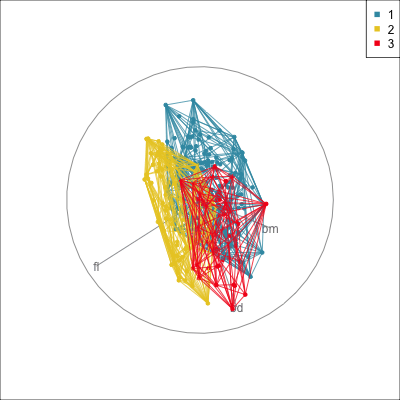
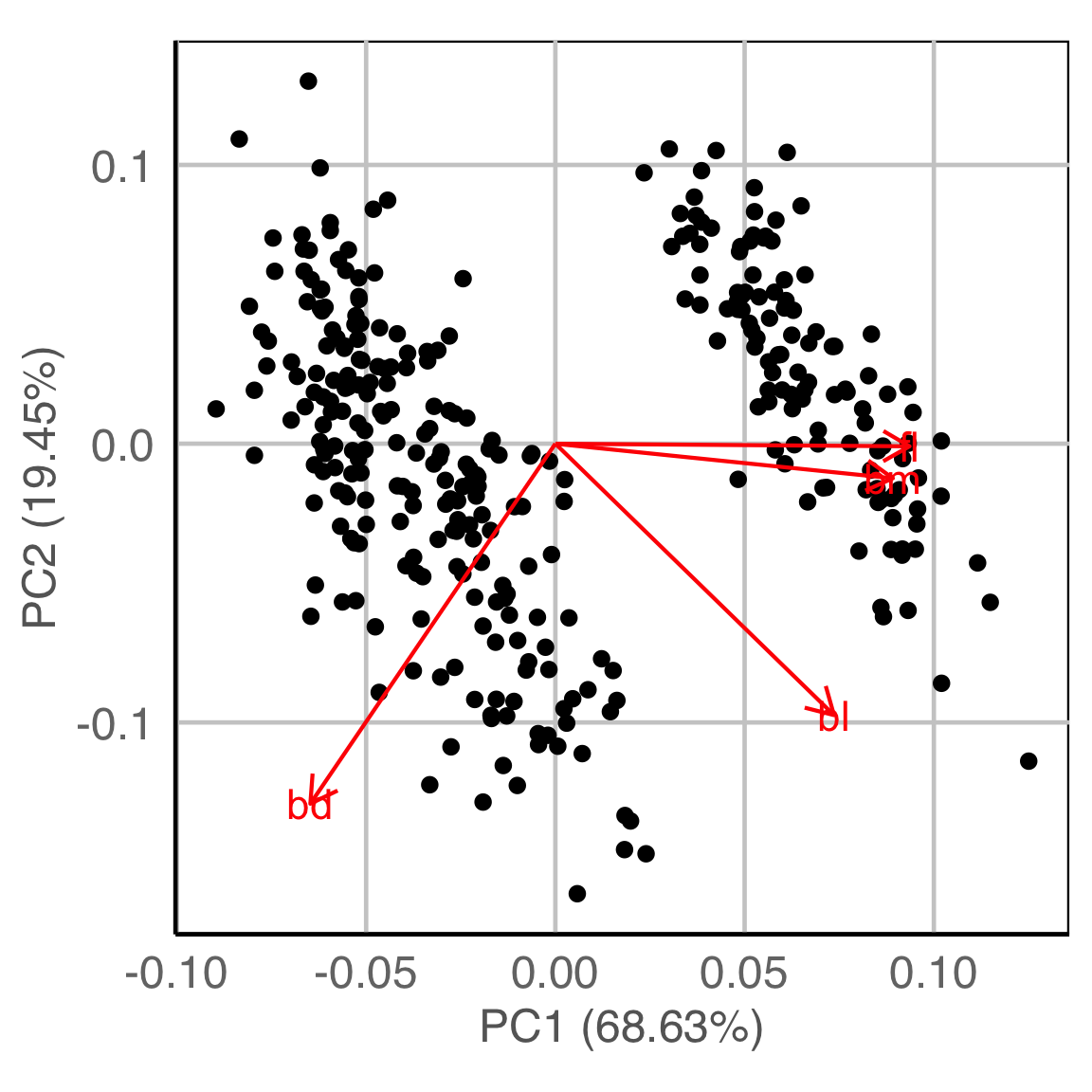
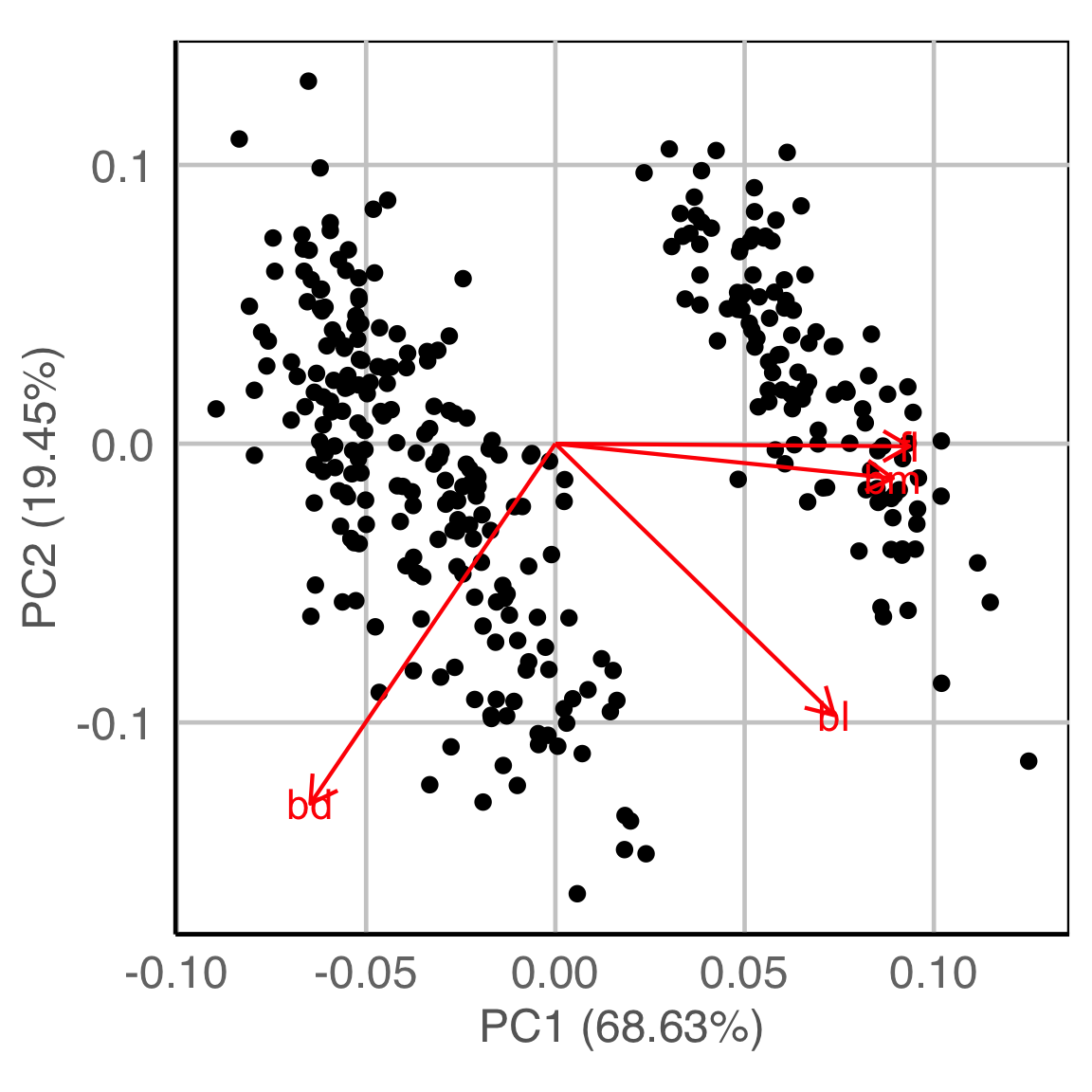
Interactivity: Compare cluster models

cl_w	cl_mc
	1	2	3
1	149	8	0
2	0	0	119
3	0	57	0

DEMO

library(crosstalk)
library(plotly)
library(viridis)
p_cl_shared <- SharedData$new(penguins_cl)

detour_plot <- detour(p_cl_shared, tour_aes(
  projection = bl:bm,
  colour = cl_w)) |>
    tour_path(grand_tour(2), 
                    max_bases=50, fps = 60) |>
       show_scatter(alpha = 0.7, axes = FALSE,
                    width = "100%", height = "450px")

conf_mat <- plot_ly(p_cl_shared, 
                    x = ~cl_mc_j,
                    y = ~cl_w_j,
                    color = ~cl_w,
                    colors = viridis_pal(option = "D")(3),
                    height = 450) |>
  highlight(on = "plotly_selected", 
              off = "plotly_doubleclick") %>%
    add_trace(type = "scatter", 
              mode = "markers")
  
bscols(
     detour_plot, conf_mat,
     widths = c(5, 6)
 )                 

Adapting to market segmentation (1/2)

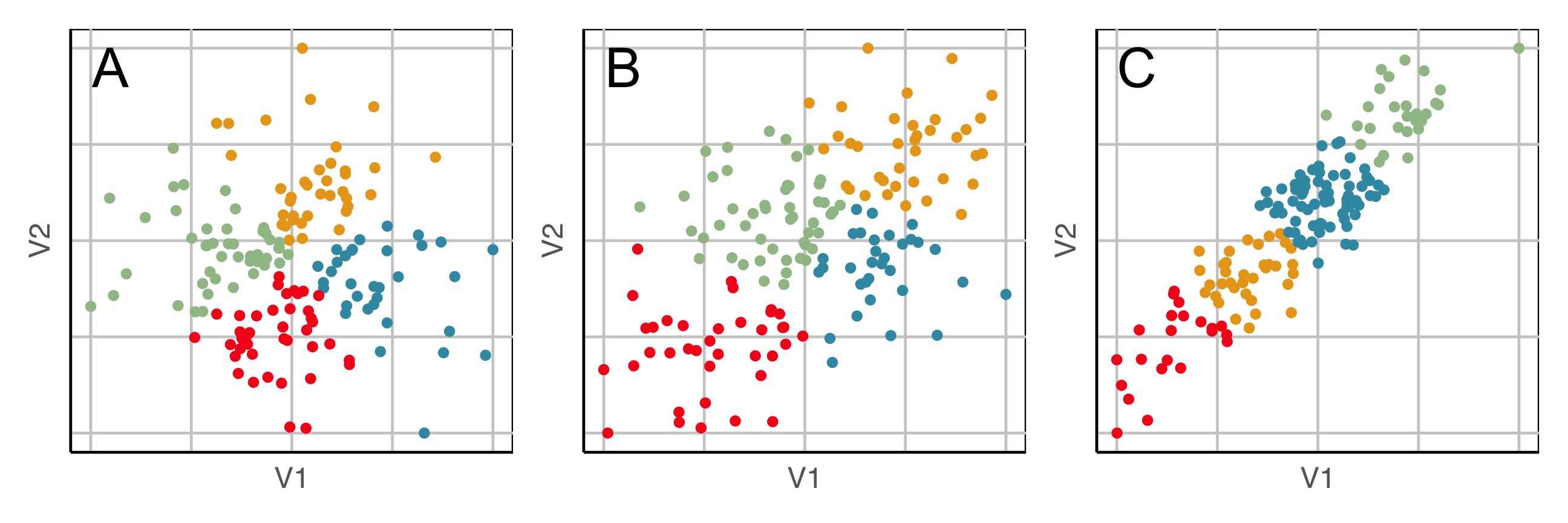
Market segmentation data typically has NO separated clusters. It is a partitioning.

Three different 2D data sets. What is a useful partition?

Adapting to market segmentation (2/2)

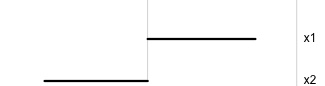
Here we show the model in the data space so we can see where it is partitioning the “blob”.

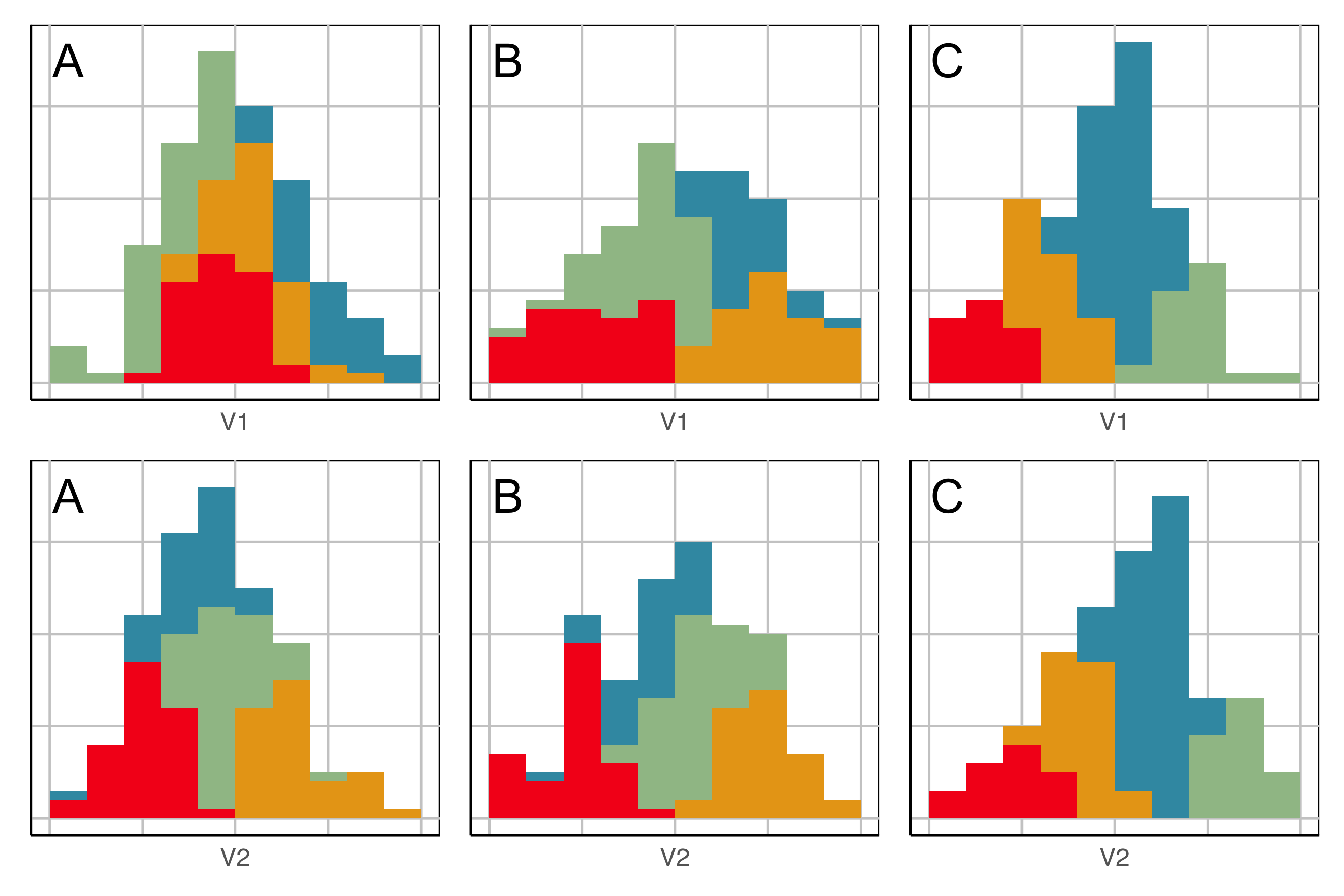
This is what the model looks like in only one variable at a time. You can’t see where it is partitioning.

Example: Tourism in Austria (1/3)

Australian Vacation Activities

• Responses from 1003 adults
• Conducted in 2007
• 44 vacation activities
• Binary response: 1 (yes), 0 (no)

Austrian Winter Activities

• Responses from 2961 adults
• 1997/98 season
• 27 activities: alpine skiing, museums, …
• Binary response: 1 (totally important), 0 (otherwise)

Data from Leisch, F., Dolnicar, S., Grün, B. (2018)

Example: Tourism in Austria (2/3)

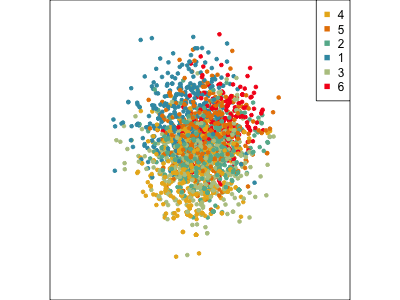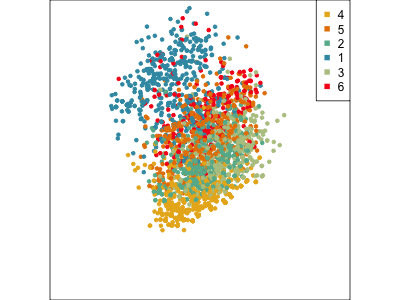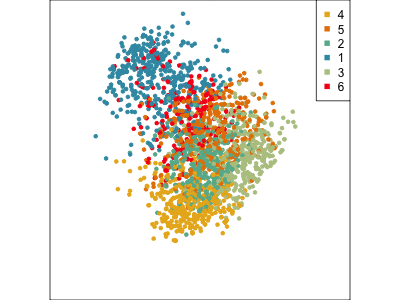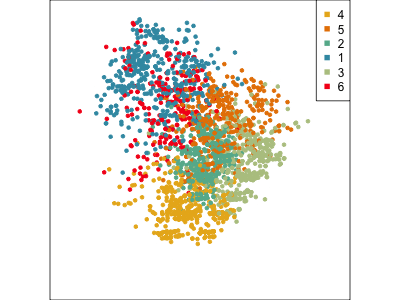
Using a guided tour. There is some hint of the partitioning, when looking at all clusters, but there is too much overlap.

Focus on two clusters only.

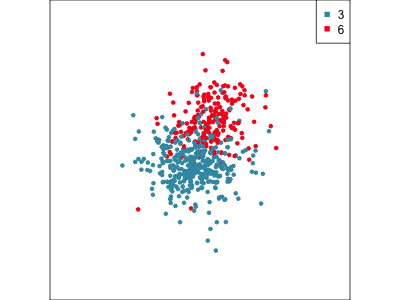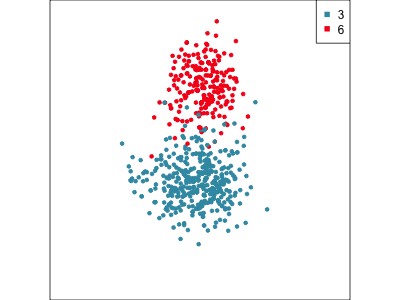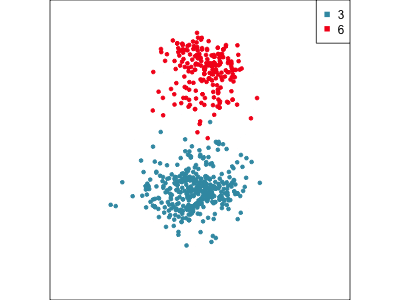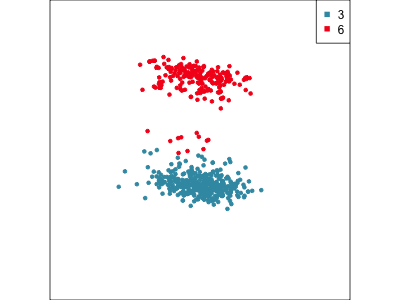
Example: Tourism in Austria (3/3)

First find the separation, then examine the combination of variables.

Cluster 6 consists of tourists who like going to health facilities, excursions and drinking wine.

# A tibble: 5 × 2
  act                       proj
  <chr>                    <dbl>
1 using.health.facilities 0.255 
2 heurigen                0.119 
3 going.to.a.spa          0.0885
4 organized.excursions    0.0841
5 excursions              0.0728

Cluster 3 consists of tourists who very much like going to a disco or bar, with some interest in alpine activities and theatre/opera.

# A tibble: 5 × 2
  act                    proj
  <chr>                 <dbl>
1 snowboarding         -0.103
2 ski.touring          -0.106
3 theater.opera        -0.119
4 alpine.skiing        -0.214
5 going.to.discos.bars -0.889

Future work, possible research

The tourr package provides the algorithm to generate the tour paths, and also create new tours, different displays.

• Stopping, pausing, going back
• Zooming in, focus on subsets
• Linking between multiple displays

Elegant interactivity solutions with detourr, liminal, langevitour, lionfish but need to be developed further.

• Better integration with model objects
• Specialist design for different models
• Integrating other guidance, explainability metrics

High-d vis intellectually challenging, and fun!

Please use these tools 😃

References and acknowledgements

• This work on market segmentation to appear in 2025 in a special issue honouring the contributions of Friedrich Leisch
• Cook and Laa (2023) Interactively exploring high-dimensional data and models in R
• Wickham et al (2015) Visualizing statistical models: Removing the blindfold
• Flatland: A Romance of Many Dimensions (1884) Edwin Abbott
• R packages: tourr, woylier, detourr, liminal, langevitour, lionfish, geozoo.

Slides made in Quarto, with code included. Available at https://dicook.github.io/MPSS/slides.html.

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.