How do we know what we don’t know? ¿Cómo sabemos lo que no sabemos?

Dianne Cook

This talk is about visualisation to help in clustering high-dimensional data

Photo by cottonbro studio

The greatest value of a data plot is when it forces us to notice what we never expected to see. ~Adapted from a Tukey quote.

Outline

• Become familiar with tour for viewing high dimensions
• Spin-and-brush
• More details of tours
• Related methods
• Clustering and tours
  • Model-based clustering
  • Summarising clusters
  • Comparing methods
  • Dimension reduction
• What we’d like to do: future research topics

Avoid cherry picking, look at all

Image: Sketchplanations

High-dimensional visualisation

Tours of high-dimensional data are like examining the shadows (projections)

(and slices/sections to see through a shadow)

Notation

Data

$$\begin{eqnarray*} X_{~n\times p} = [X_{~1}~X_{~2}~\dots~X_{~p}]_{~n\times p} = \left[ \begin{array}{cccc} x_{~11} & x_{~12} & \dots & x_{~1p} \\ x_{~21} & x_{~22} & \dots & x_{~2p}\\ \vdots & \vdots & & \vdots \\ x_{~n1} & x_{~n2} & \dots & x_{~np} \end{array} \right]_{~n\times p} \end{eqnarray*}$$

Notation

Projection

$$\begin{eqnarray*} A_{~p\times d} = \left[ \begin{array}{cccc} a_{~11} & a_{~12} & \dots & a_{~1d} \\ a_{~21} & a_{~22} & \dots & a_{~2d}\\ \vdots & \vdots & & \vdots \\ a_{~p1} & a_{~p2} & \dots & a_{~pd} \end{array} \right]_{~p\times d} \end{eqnarray*}$$

Notation

Projected data

$$\begin{eqnarray*} Y_{~n\times d} = XA = \left[ \begin{array}{cccc} y_{~11} & y_{~12} & \dots & y_{~1d} \\ y_{~21} & y_{~22} & \dots & y_{~2d}\\ \vdots & \vdots & & \vdots \\ y_{~n1} & y_{~n2} & \dots & y_{~nd} \end{array} \right]_{~n\times d} \end{eqnarray*}$$

High-dimensional visualisation

Data is 2D: $~~p=2$

Projection is 1D: $~~d=1$

$$\begin{eqnarray*} A_{~2\times 1} = \left[ \begin{array}{c} a_{~11} \\ a_{~21}\\ \end{array} \right]_{~2\times 1} \end{eqnarray*}$$

Notice that the values of $A$ change between (-1, 1). All possible values being shown during the tour.

$$\begin{eqnarray*} A = \left[ \begin{array}{c} 1 \\ 0\\ \end{array} \right] ~~~~~~~~~~~~~~~~ A = \left[ \begin{array}{c} 0.7 \\ 0.7\\ \end{array} \right] ~~~~~~~~~~~~~~~~ A = \left[ \begin{array}{c} 0.7 \\ -0.7\\ \end{array} \right] \end{eqnarray*}$$

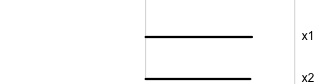
watching the 1D shadows we can see:

• unimodality
• bimodality, there are two clusters.

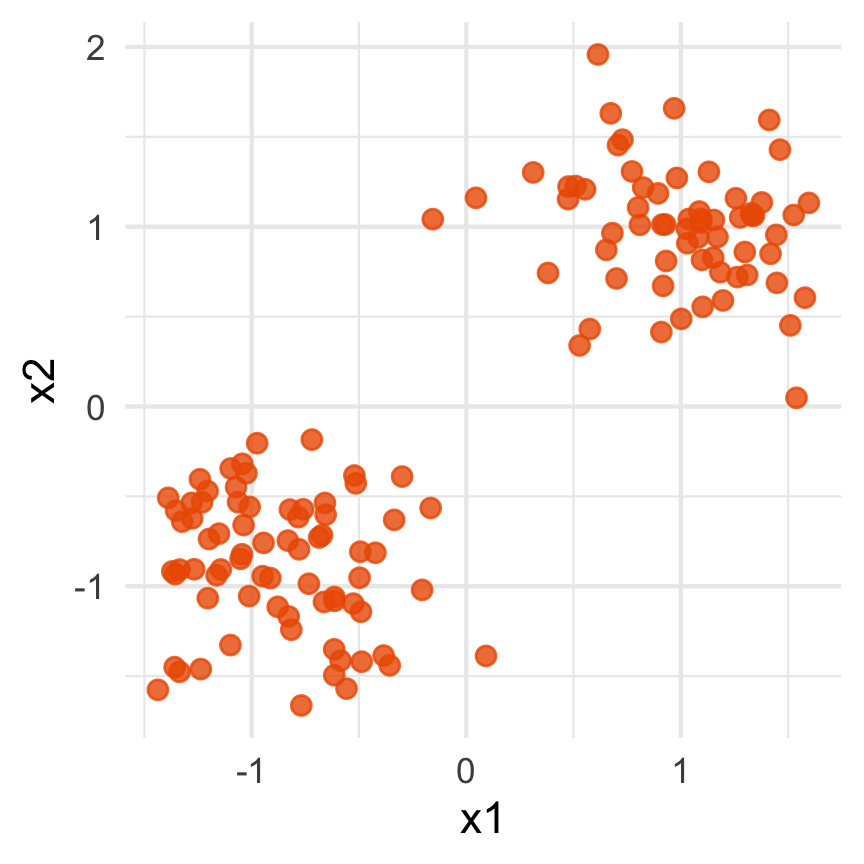
What does the 2D data look like? Can you sketch it?

High-dimensional visualisation

⟵
The 2D data

High-dimensional visualisation

Data is 3D: $p=3$

Projection is 2D: $d=2$

$$\begin{eqnarray*} A_{~3\times 2} = \left[ \begin{array}{cc} a_{~11} & a_{~12} \\ a_{~21} & a_{~22}\\ a_{~31} & a_{~32}\\ \end{array} \right]_{~3\times 2} \end{eqnarray*}$$

Notice that the values of $A$ change between (-1, 1). All possible values being shown during the tour.

See:

• circular shapes
• some transparency, reveals middle
• hole in in some projections
• no clustering

High-dimensional visualisation

Data is 4D: $p=4$

Projection is 2D: $d=2$

$$\begin{eqnarray*} A_{~4\times 2} = \left[ \begin{array}{cc} a_{~11} & a_{~12} \\ a_{~21} & a_{~22}\\ a_{~31} & a_{~32}\\ a_{~41} & a_{~42}\\ \end{array} \right]_{~4\times 2} \end{eqnarray*}$$

How many clusters do you see?

• three, right?
• one separated, and two very close,
• and they each have an elliptical shape.

• do you also see an outlier or two?

Well done!

You can now tell everyone that you can SEE in 4D!

Method 1: Spin-and-brush

If you want to discover and mark the clusters you see, you can use the detourr package to spin and brush points. Here’s a live demo. Hopefully this works.

library(detourr)
set.seed(645)
detour(penguins_sub[,1:4], 
       tour_aes(projection = bl:bm)) |>
       tour_path(grand_tour(2), fps = 60, 
                 max_bases=40) |>
       show_scatter(alpha = 0.7, 
                    axes = FALSE)

DEMO

Tour architecture

• Data: $p$-D
• Projection dimension: choose $d$
• Rendering method: histogram, density plot, scatterplot, …

Algorithm:

• Path taken through high-dimensions: random, guided, local, little, manual
• Interpolation method: geodesic (plane to plane), Givens (basis to basis)

Software:

$~~$ $~~$ $~~$ $~~$

Types of tours

Grand tour

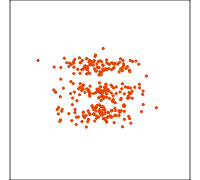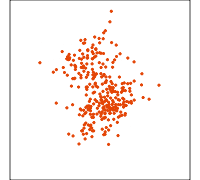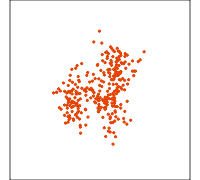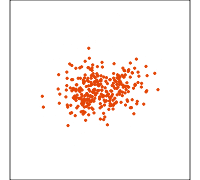
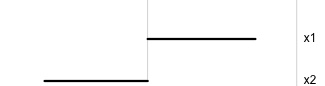
Slice display

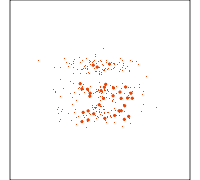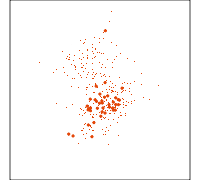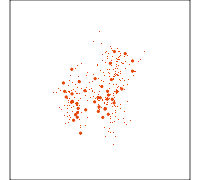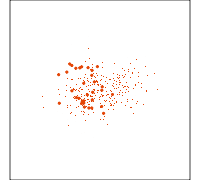
Guided tour

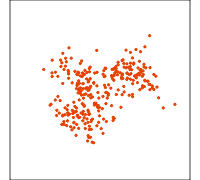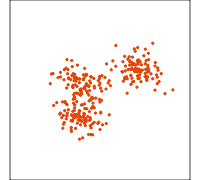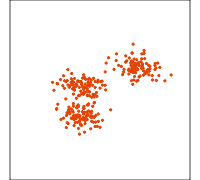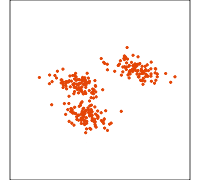
Local tour

Related methods

PCA

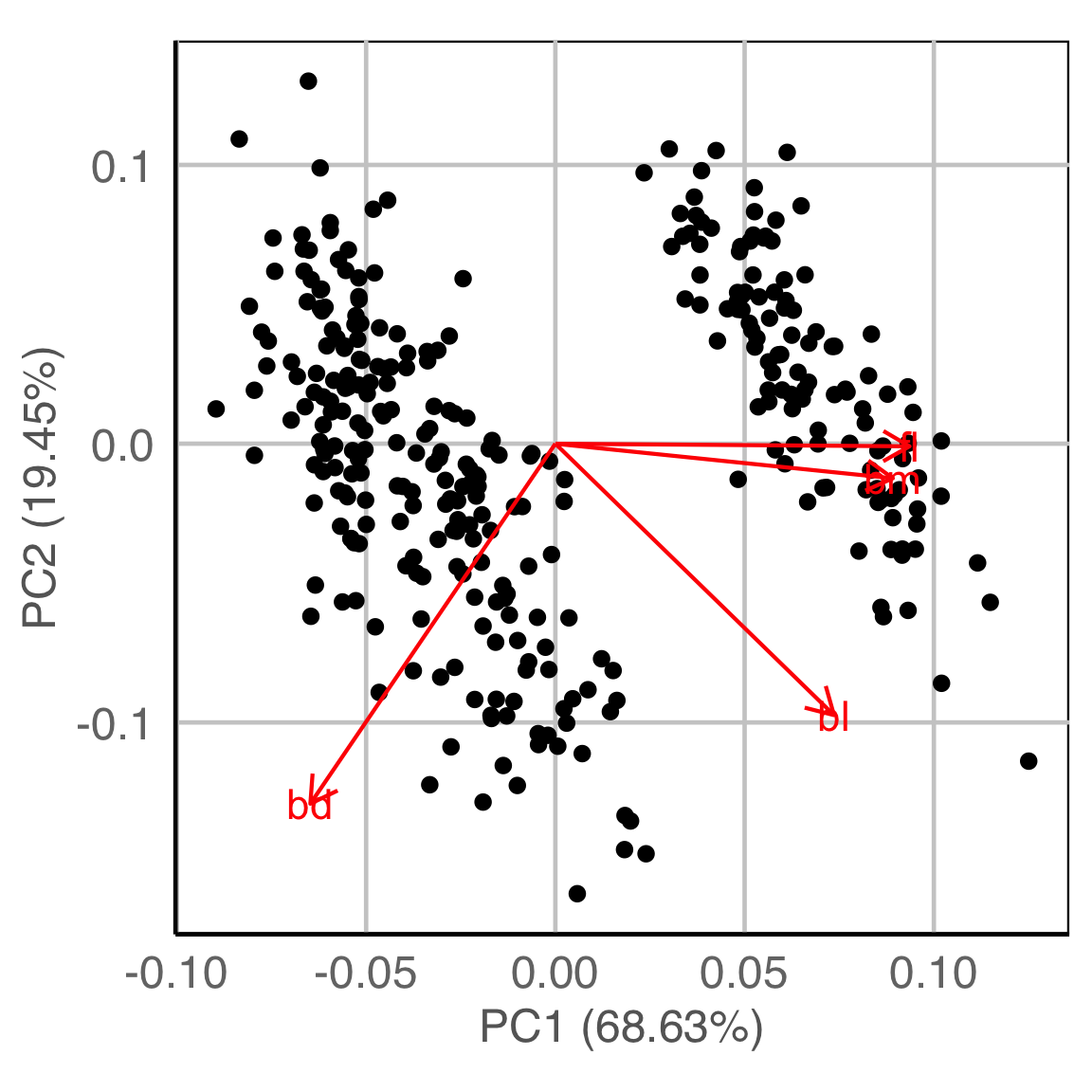
NLDR: tSNE

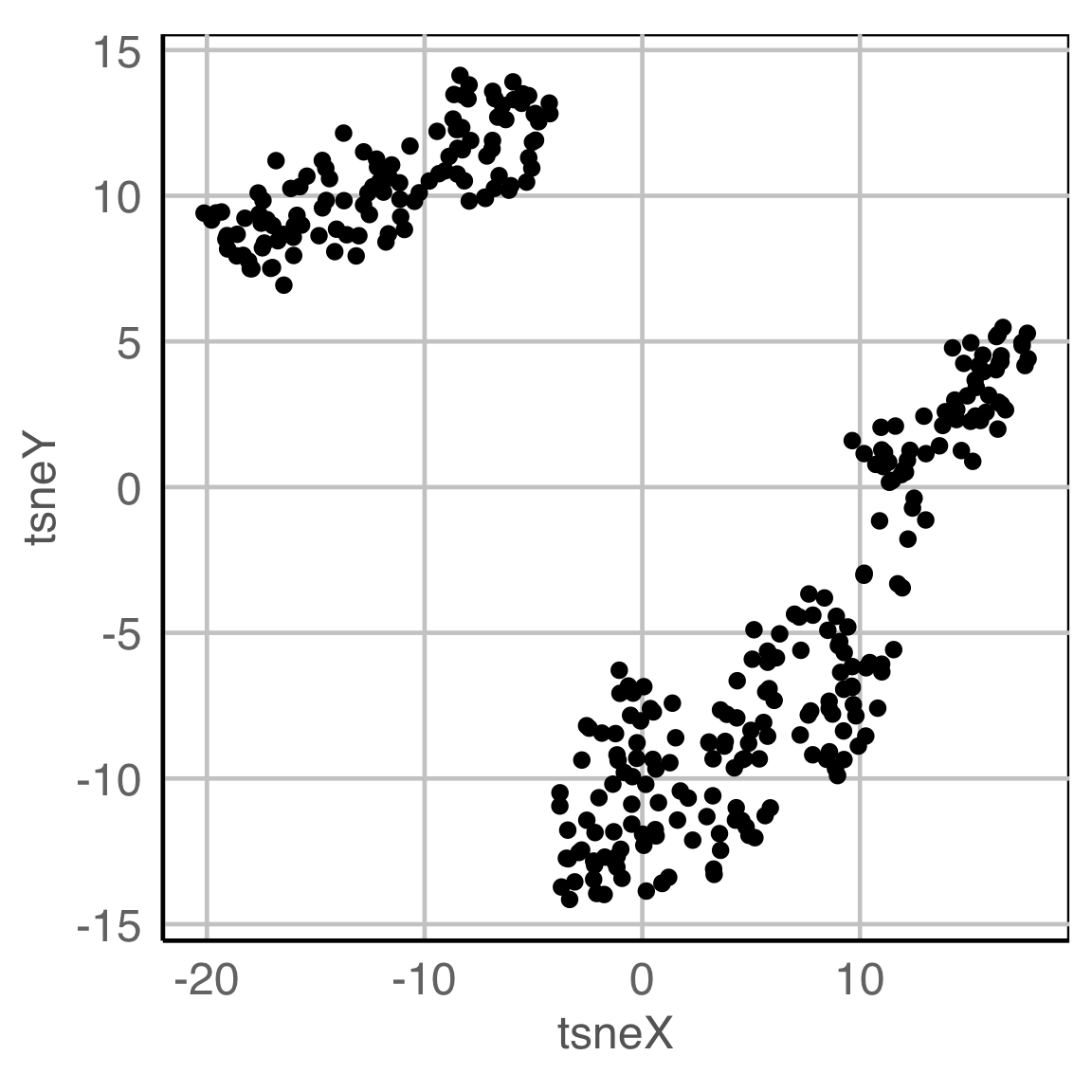
Clustering & tours

Model-based - 2D (1/3)

Table of model types

Model-based - 4D (2/3)

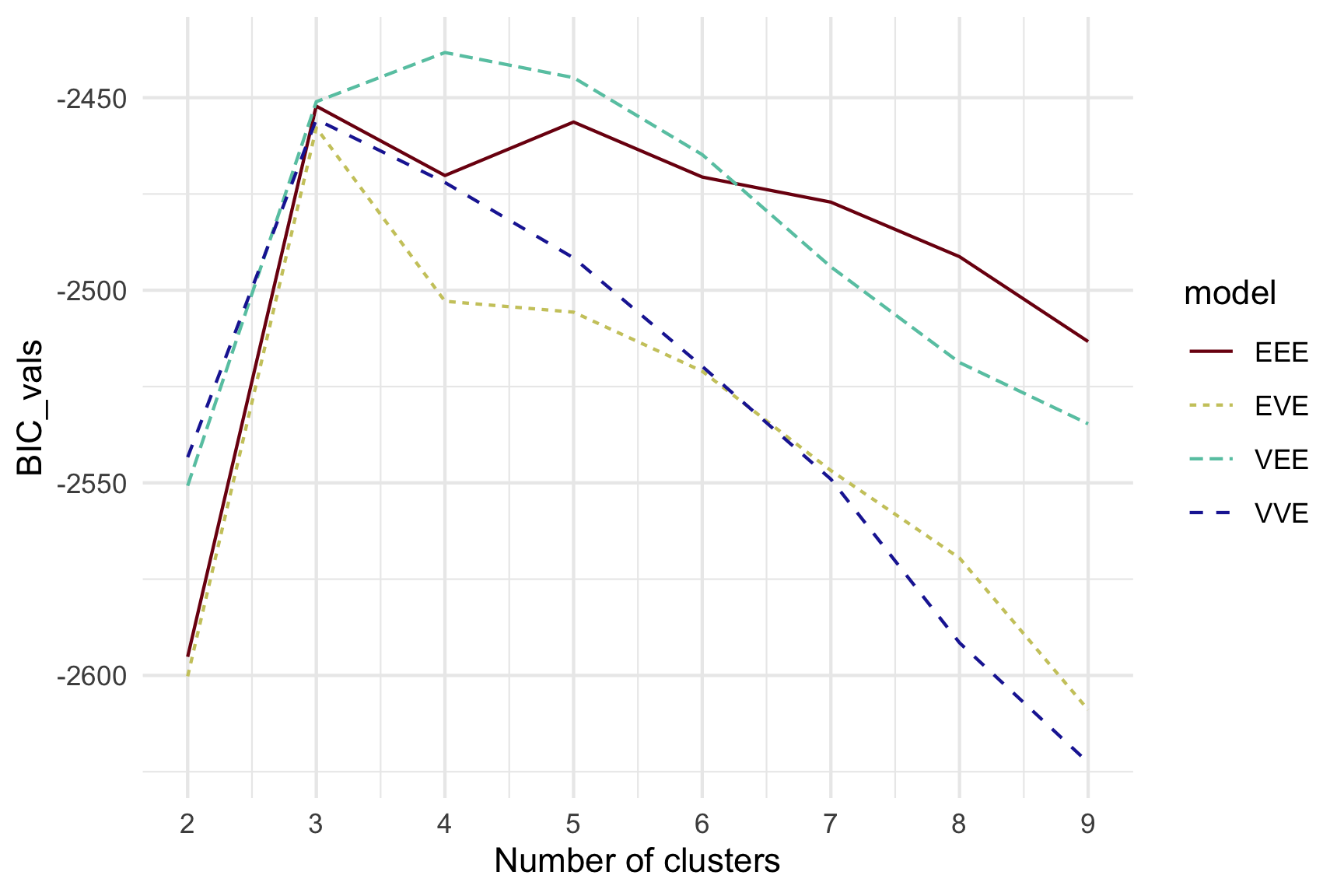
Model-based (3/3) ~~Which fits the data better?

Best model: four-cluster VEE

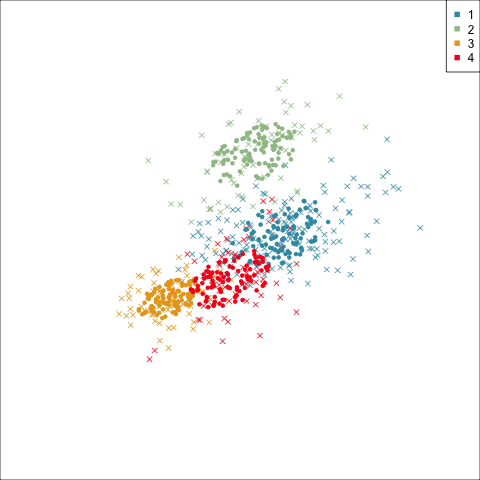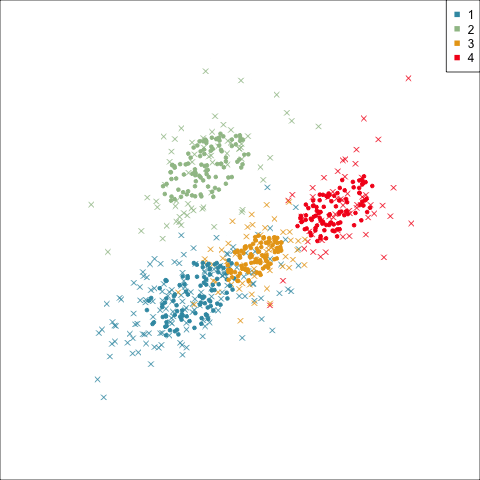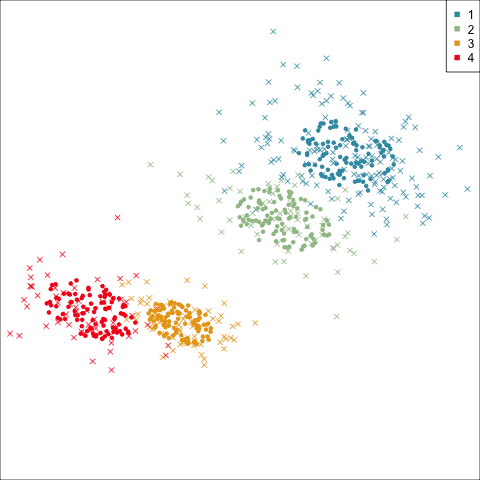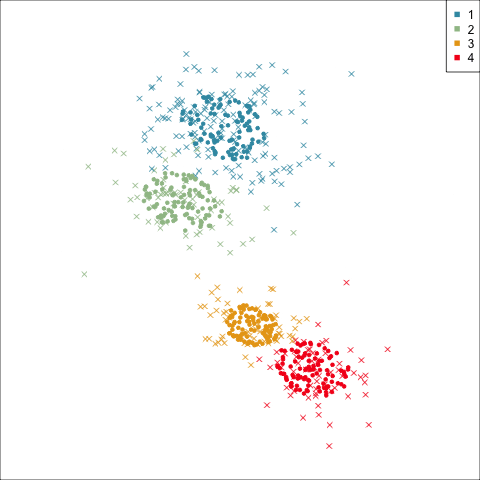
Three-cluster EEE

Table of model types

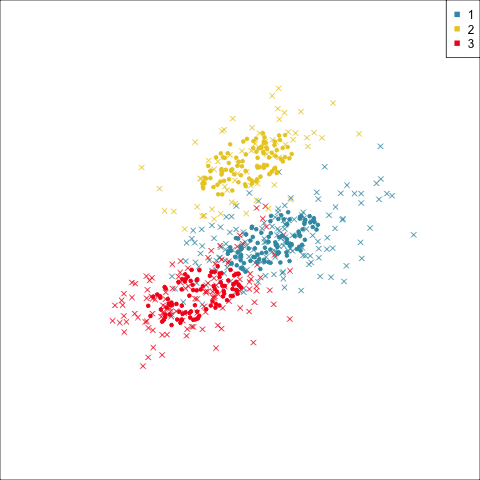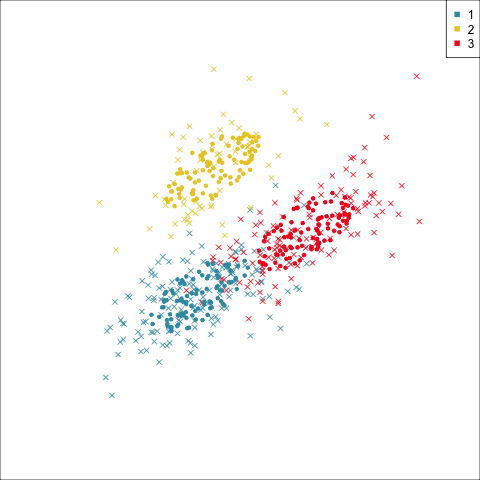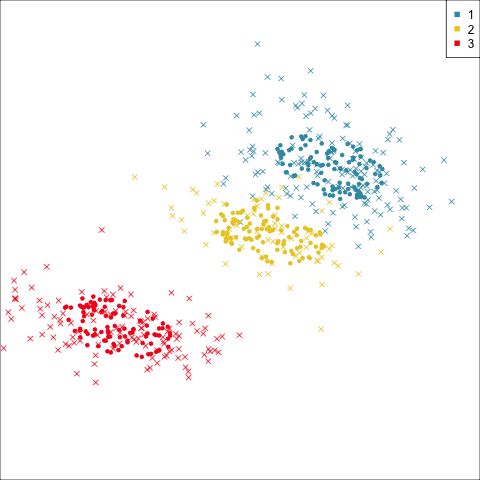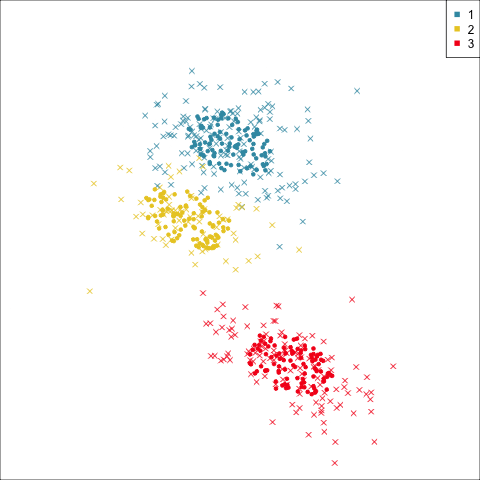
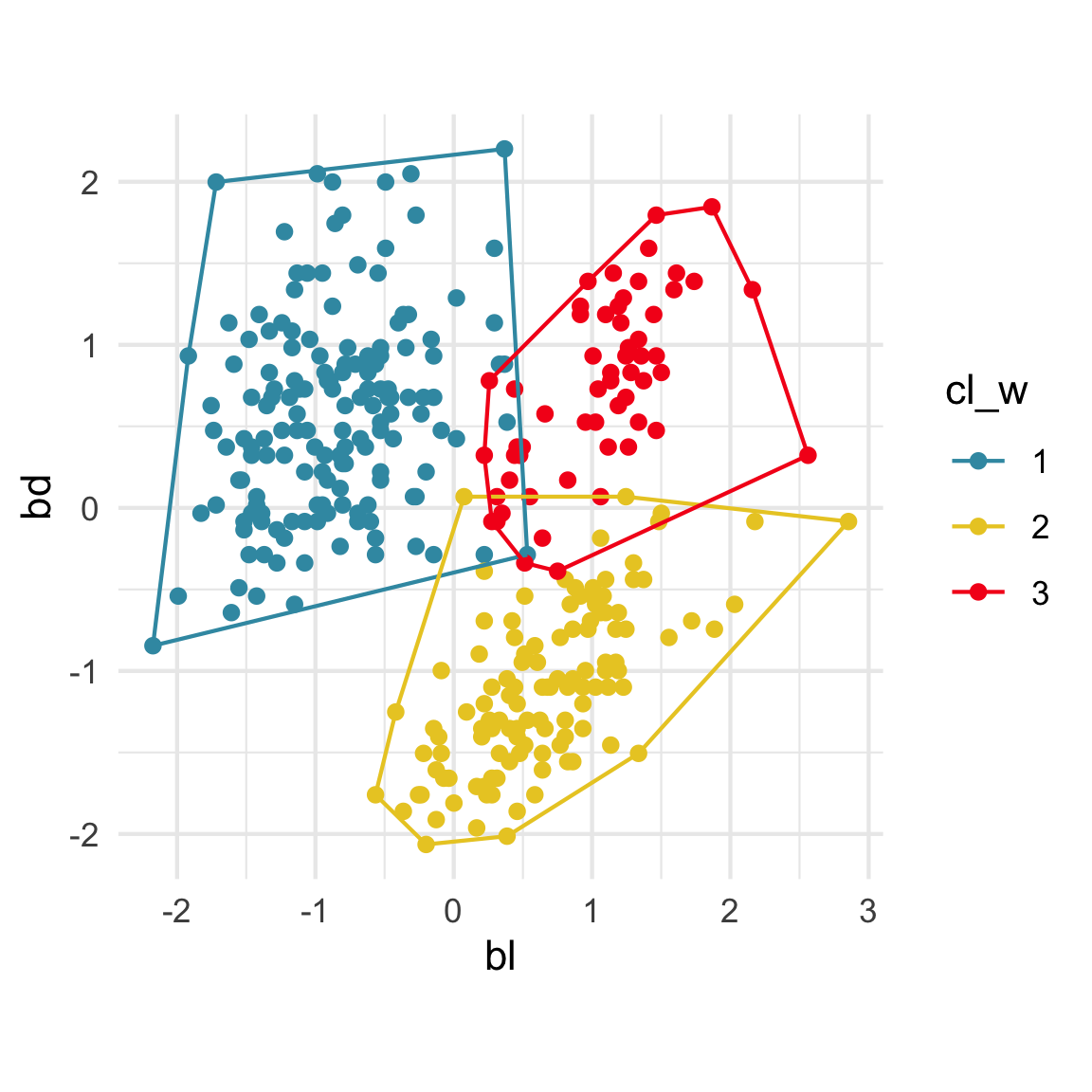
Summarising clusters

Convex hulls are often used to summarise clusters in 2D. It is possible to view these in high-d, too.

Ward’s linkage hierarchical clustering

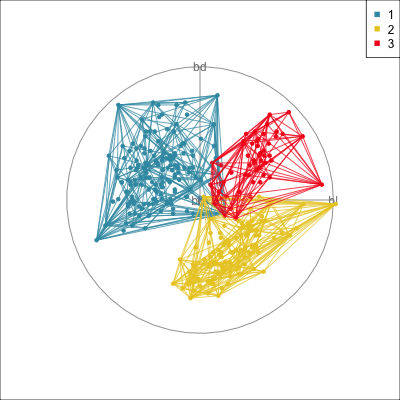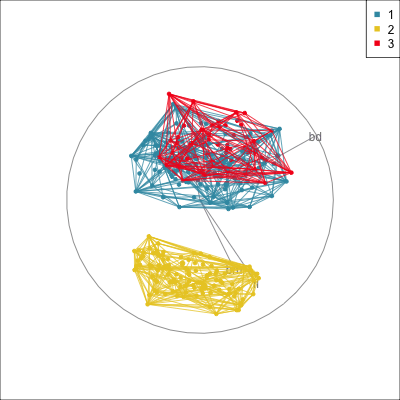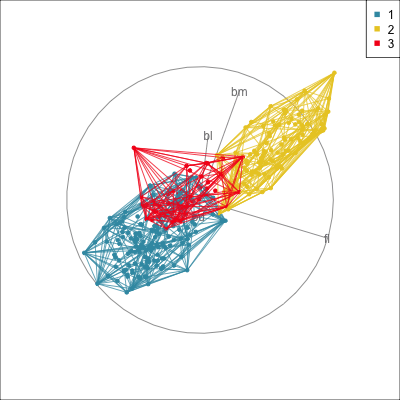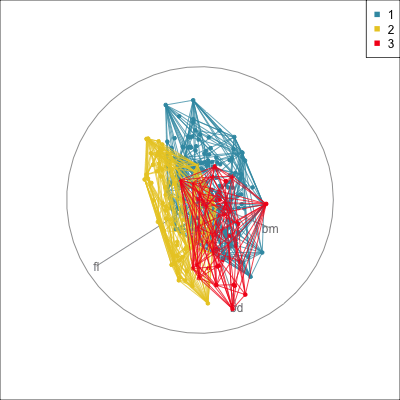
Comparing methods

cl_w	cl_mc
	1	2	3
1	149	8	0
2	0	0	119
3	0	57	0

DEMO

library(crosstalk)
library(plotly)
library(viridis)
p_cl_shared <- SharedData$new(penguins_cl)

detour_plot <- detour(p_cl_shared, tour_aes(
  projection = bl:bm,
  colour = cl_w)) |>
    tour_path(grand_tour(2), 
                    max_bases=50, fps = 60) |>
       show_scatter(alpha = 0.7, axes = FALSE,
                    width = "100%", height = "450px")

conf_mat <- plot_ly(p_cl_shared, 
                    x = ~cl_mc_j,
                    y = ~cl_w_j,
                    color = ~cl_w,
                    colors = viridis_pal(option = "D")(3),
                    height = 450) |>
  highlight(on = "plotly_selected", 
              off = "plotly_doubleclick") %>%
    add_trace(type = "scatter", 
              mode = "markers")
  
bscols(
     detour_plot, conf_mat,
     widths = c(5, 6)
 )                 

Dimension reduction

limn_tour_link(
  p_tsne_df,
  penguins_sub,
  cols = bl:bm,
  color = species
)

DEMO

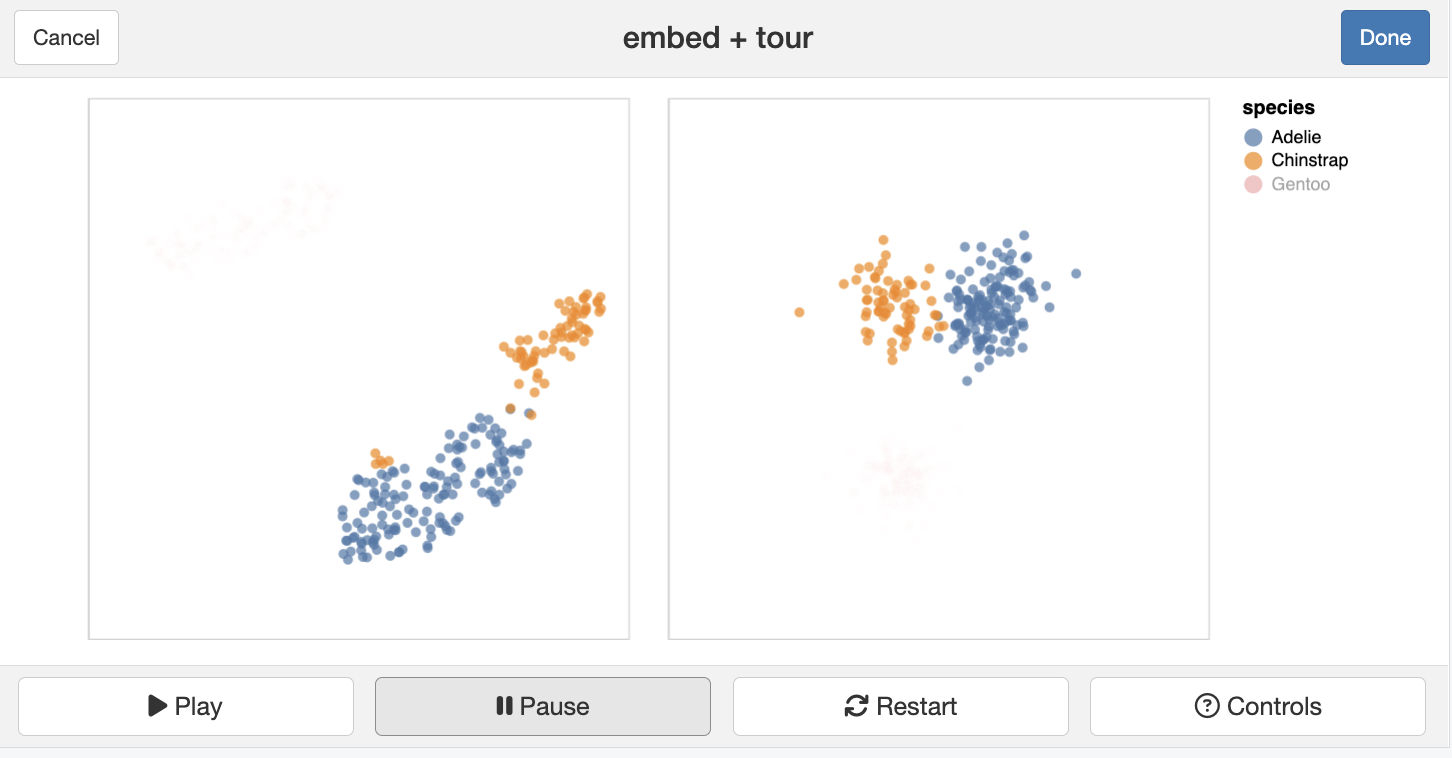
What we can’t do, that we’d like to

The tourr package provides the algorithm to generate the tour paths, and also create new tours, different displays. However, the interactivity is poor, which is a big limitation.

• Stopping, pausing, going back
• Zooming in, focus on subsets
• Linking between multiple displays

detourr is an elegant solution, which could be developed further.

• Better integration with model objects
• Specialist design for different models
• Integrating other guidance, explainability metrics

Vis is fun!

References and acknowledgements

• Cook and Laa (2023) Interactively exploring high-dimensional data and models in R
• Slides made in Quarto.
• Get a copy of slides at https://github.com/dicook/LatinR

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.