Shadows of Data

Visualising the Geometry of High Dimensions

Dianne Cook
Econometrics and Business Statistics
Monash University

You can’t see beyond 3D!

You can’t see beyond 3D!

We are going to see that we can gain intuition for structure in high dimensions through visualisation

The greatest value of a data plot is when it forces us to notice what we never expected to see. ~Adapted from a Tukey quote.

It doesn’t mean that it’s easy. It doesn’t mean that visualisation is used alone. It means that (high-dimensional) visualisation is an important part of your toolbox, especially to allow discovery of what we don’t know.

Outline

• Intuitive explanation of a tour (and 18th century novel)
• Construction of a tour
• Connection to manifolds (and work at U.Adelaide)
• Why?
• Algorithms in the tourr package
• New developments in recent years
• Showing the model in the data space

• Examples
  • dimension reduction
  • understanding clustering
  • comparing classification boundaries
  • departures from multivariate normal
  • de-constructing neural network fits
  • ternary diagrams beyond 2D

High-dimensional visualisation using shadows

Tours of high-dimensional data are like examining the shadows (projections)

(and slices/sections to see through a shadow)

What “high dimensions” means in statistics

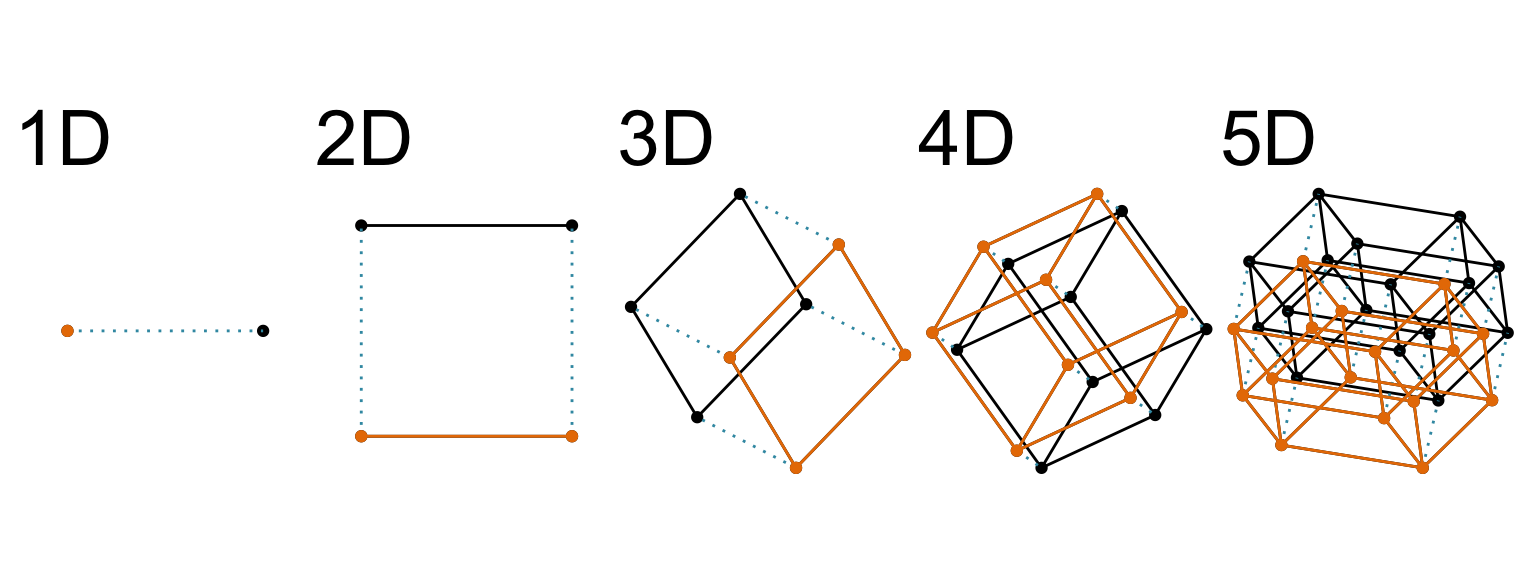
Increasing dimension adds an additional orthogonal axis.

If you want more high-dimensional shapes there is an R package, geozoo, which will generate cubes, spheres, simplices, mobius strips, torii, boy surface, klein bottles, cones, various polytopes, …

And read or watch Flatland: A Romance of Many Dimensions (1884) Edwin Abbott.

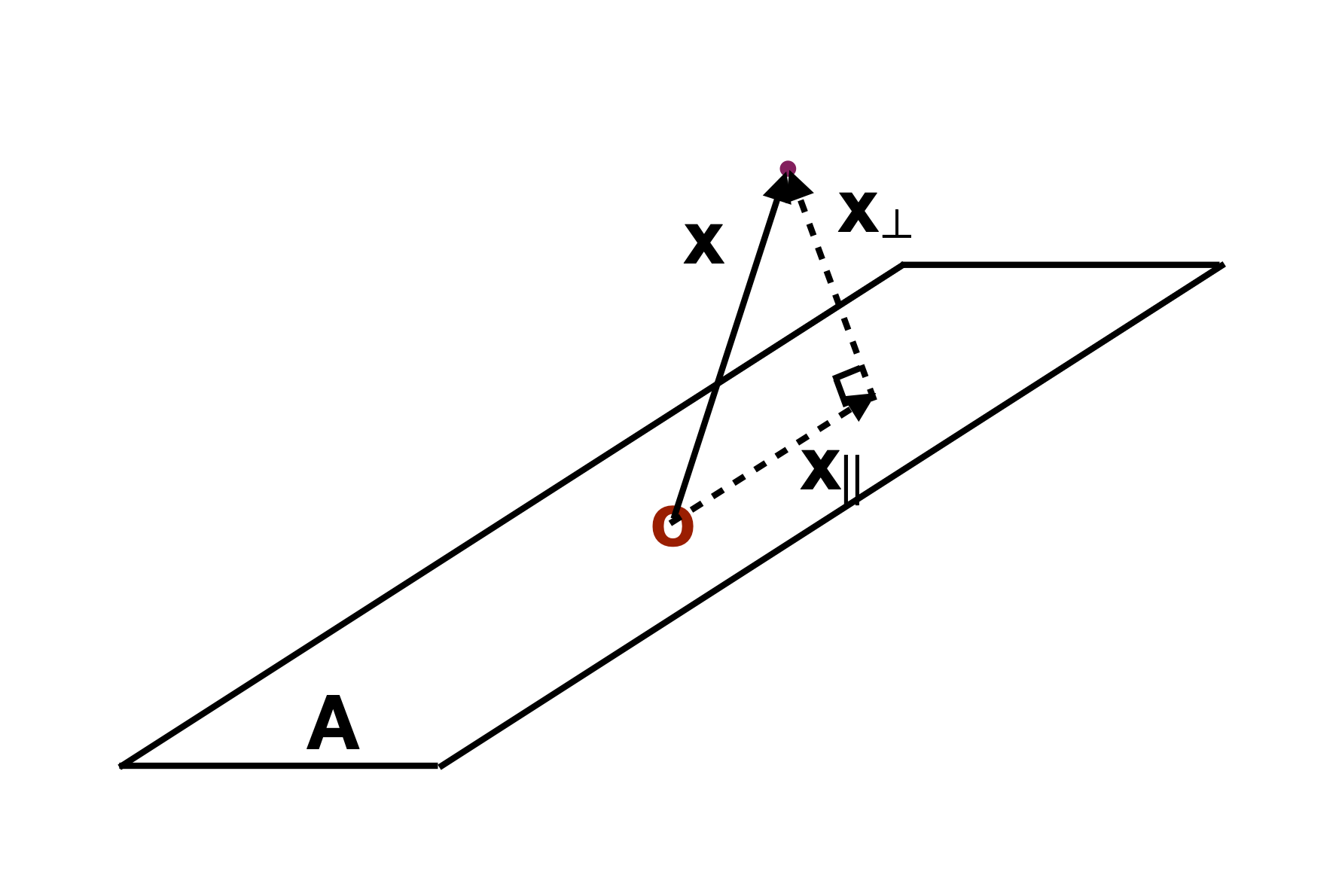
Notation

• Data
• Projection basis
• Projected data

$$\begin{eqnarray*} X_{~n\times p} = [X_{~1}~X_{~2}~\dots~X_{~p}]_{~n\times p} = \left[ \begin{array}{cccc} x_{~11} & x_{~12} & \dots & x_{~1p} \\ x_{~21} & x_{~22} & \dots & x_{~2p}\\ \vdots & \vdots & & \vdots \\ x_{~n1} & x_{~n2} & \dots & x_{~np} \end{array} \right]_{~n\times p} \end{eqnarray*}$$

$$\begin{eqnarray*} A_{~p\times d} = \left[ \begin{array}{cccc} a_{~11} & a_{~12} & \dots & a_{~1d} \\ a_{~21} & a_{~22} & \dots & a_{~2d}\\ \vdots & \vdots & & \vdots \\ a_{~p1} & a_{~p2} & \dots & a_{~pd} \end{array} \right]_{~p\times d} \end{eqnarray*}$$

$$\begin{eqnarray*} Y_{~n\times d} = XA = \left[ \begin{array}{cccc} y_{~11} & y_{~12} & \dots & y_{~1d} \\ y_{~21} & y_{~22} & \dots & y_{~2d}\\ \vdots & \vdots & & \vdots \\ y_{~n1} & y_{~n2} & \dots & y_{~nd} \end{array} \right]_{~n\times d} \end{eqnarray*}$$

1D projections to see 2D

• 1D projections
• The full 2D

Data is 2D: $~~p=2$

Projection is 1D: $~~d=1$

$$\begin{eqnarray*} A_{~2\times 1} = \left[ \begin{array}{c} a_{~11} \\ a_{~21}\\ \end{array} \right]_{~2\times 1} \end{eqnarray*}$$

Notice that the values of $A$ change between (-1, 1). All possible values being shown during the tour.

$$\begin{eqnarray*} A = \left[ \begin{array}{c} 1 \\ 0\\ \end{array} \right] ~~~~~~~~~~~~~~~~ A = \left[ \begin{array}{c} 0.7 \\ 0.7\\ \end{array} \right] ~~~~~~~~~~~~~~~~ A = \left[ \begin{array}{c} 0.7 \\ -0.7\\ \end{array} \right] \end{eqnarray*}$$

watching the 1D shadows we can see:

• unimodality
• bimodality, there are two clusters.

What does the 2D data look like? Can you sketch it?

2D projections to see 4D

• Clusters
• Labelled
• Only 2D
• Misses

Data is 4D: $p=4$

Projection is 2D: $d=2$

$$\begin{eqnarray*} A_{~4\times 2} = \left[ \begin{array}{cc} a_{~11} & a_{~12} \\ a_{~21} & a_{~22}\\ a_{~31} & a_{~32}\\ a_{~41} & a_{~42}\\ \end{array} \right]_{~4\times 2} \end{eqnarray*}$$

How many clusters do you see?

• three, right?
• one separated, and two very close,
• and they each have an elliptical shape.

• do you also see an outlier or two?

Species explains the three clusters.

Best view

Weird Gentoo

Weird Chinstrap

More anomalies

Algorithms in the tourr package

Tours have two main components: How to move over the space, and how to display the projected data.

Movement

• choice of target planes
  • grand: random
  • guided: objective function
  • local: nearby
  • little: marginals
  • manual/radial: specific variable
• interpolation between them
  • geodesic: plane to plane (Grassmann manifold)
  • Givens: frame/basis to frame/basis (Stiefel manifold)

Display

How should you plot your projected data?

• 1D: density, dotplot, histogram
• 2D: scatterplot, density2D, sage, pca, slice
• 3D: stereo
• kD: parallel coordinates, scatterplot matrix
• 1D+spatial: image

The packages detourr, liminal and lionfish take the path produced by tourr functions.

Connection to work at U. Adelaide

James, A. T. and Constantine, A. G. (1974) Generalized Jacobi Polynomials as Spherical Functions of the Grassmann Manifold, https://doi.org/10.1112/plms/s3-29.1.174

• theoretical foundation for understanding the distribution theory underlying multivariate statistics for hypothesis testing
• was useful for developing the projection pursuit guided algorithm built on indexes derived from Hermite polynomials
• the tour can be used to understand how these test statistics relate to the data: Hotellings $T^2$, Wilks $\Lambda$, Hotelling-Lawley trace, Roy’s largest root

Early tour algorithms

• 3D
• 4D
• Two movement types

1D paths on 3D space

2D paths on 3D space

1D paths on 4D space

2D paths on 4D space

Grand tour: see from all sides

Guided tour: Steer towards the most interesting features.

Recent developments

• interactivity: detourr, liminal, langevitour, lionfish
• slice/section: explore shape of models
• manual/radial tour: explore sensitivity of structure to particular variables
• sage: correct for piling
• Givens interpolation: frame to frame. Generally want geodesic interpolation because it removes the distracting within plane spin but sometimes it is important to move to exact projection.
• anomaly tour: compare your sample to a multivariate normal

Slice

Utilise distance from the projection plane to make the slice, and shift centre of projection plane.

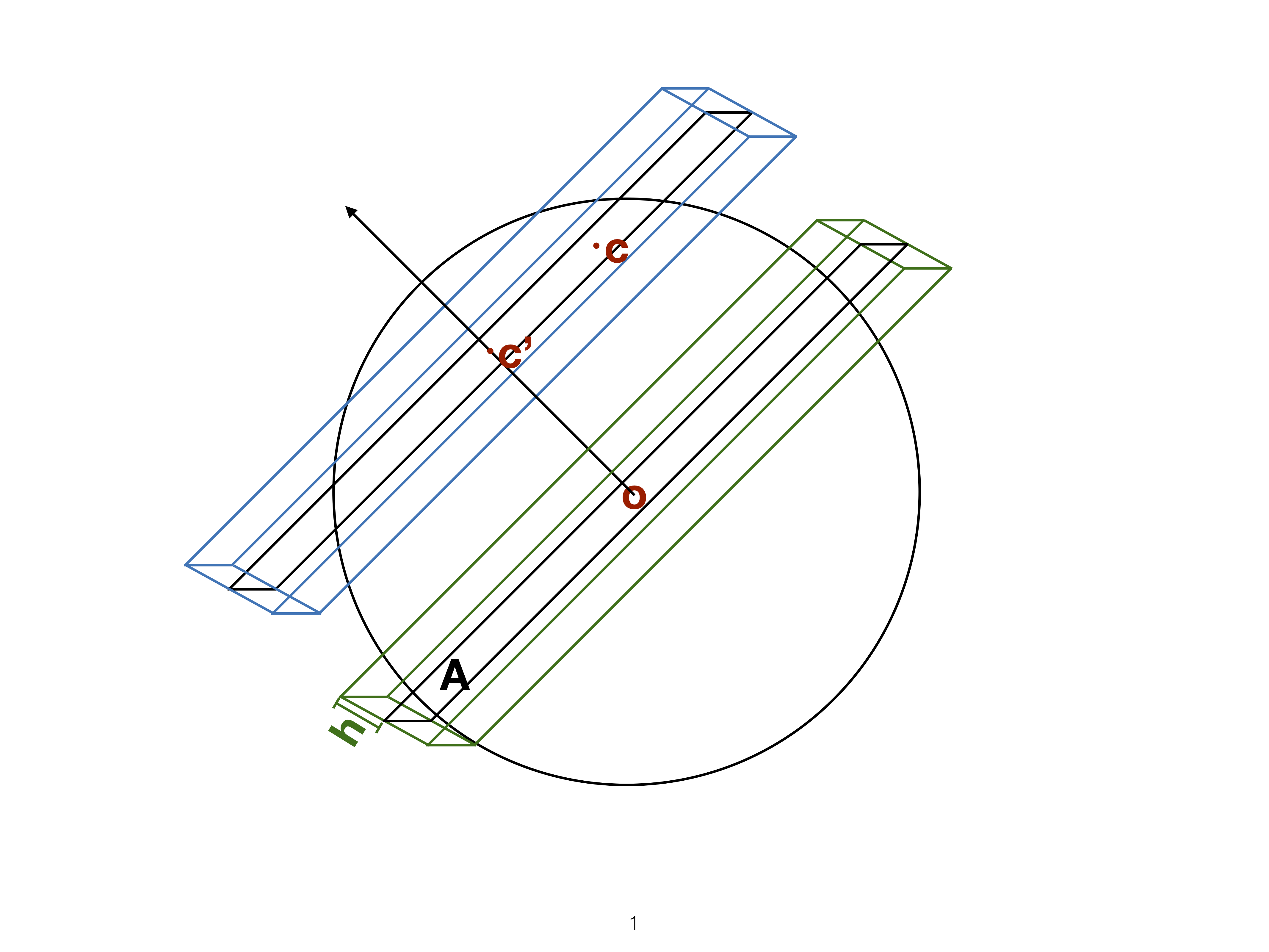
Slice tour

• Torus 3D
• Torus 4D
• Hollow?
• or solid?

Projection

Slice

Projection

Slice

Sage transformation (1/2)

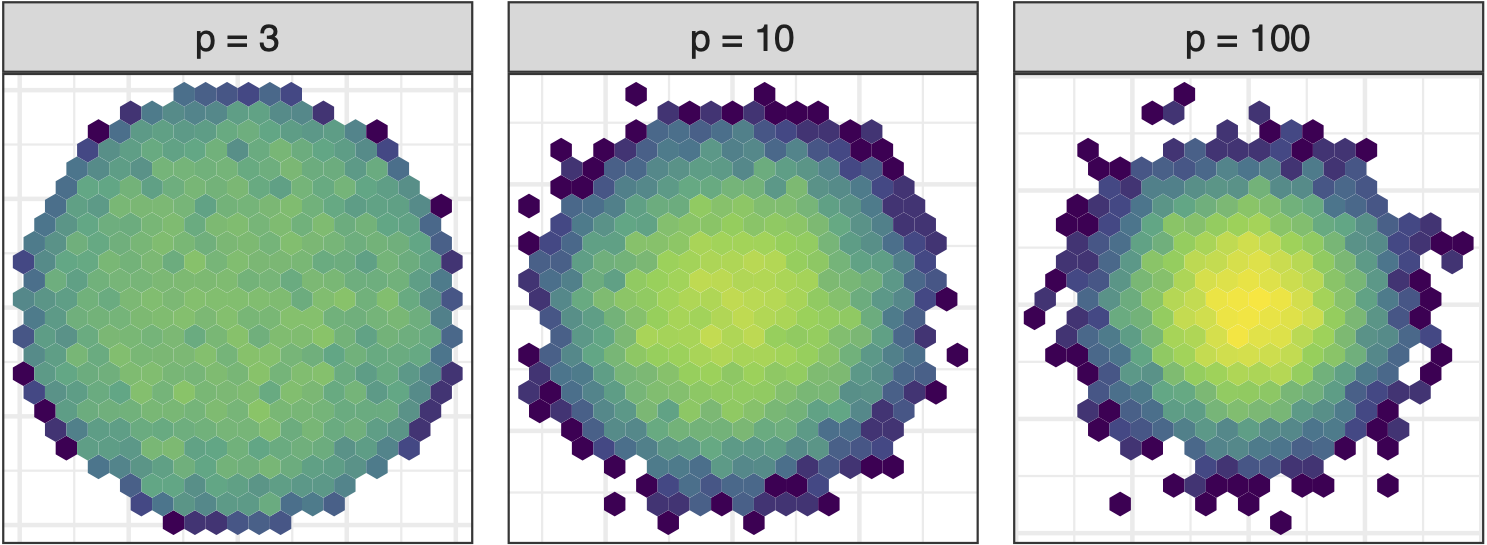
As number of variables increase concentration in centre of projection increases. Great for studying distribution of means (Central Limit Theorem) but bad for visualising high-dimensional data. Possibly obscures interesting structure.

Sage transformation (2/2)

2D projections of 10D sphere

Sage transformation on projected data

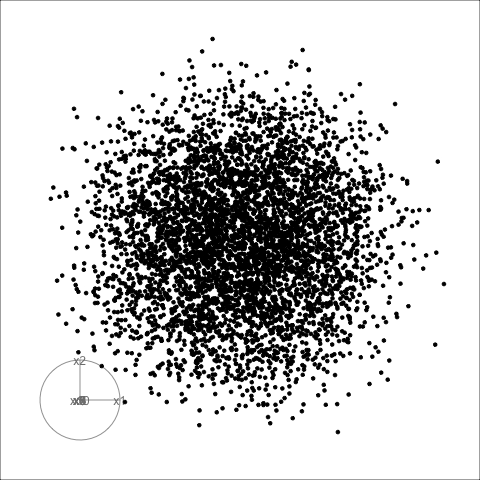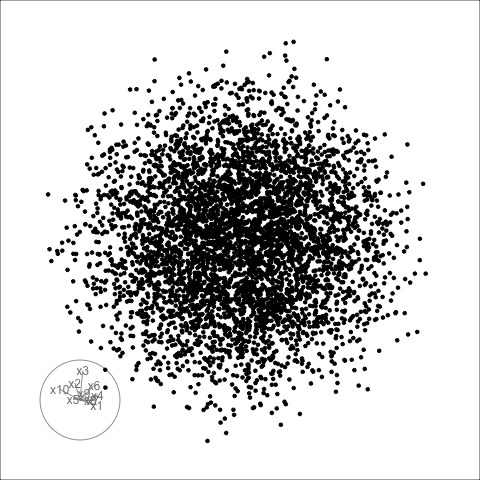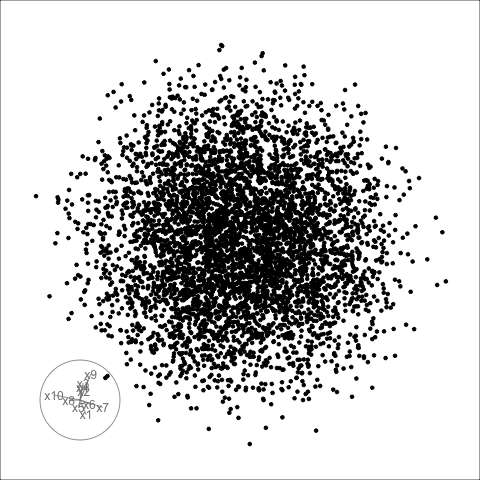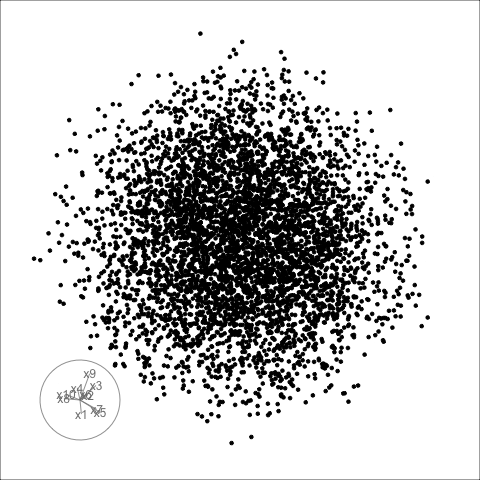
Givens interpolation (1/2)

TARGET BASIS (would show dog if we could find)

Grassmann——————————Stiefel

Givens interpolation (2/2)

——–Givens—–geodesic

Givens interpolation ends at requested frame, but geodesic interpolation arrives at the plane, is frame-agnostic, and that is problematic for optimisation using the guided tour.

Interactivity: exploration

If you want to discover and mark the clusters you see, you can use the detourr package to spin and brush points. Here’s a live demo. Hopefully this works.

library(detourr)
set.seed(645)
detour(penguins_sub[,1:4], 
       tour_aes(projection = bl:bm)) |>
       tour_path(grand_tour(2), fps = 60, 
                 max_bases=40) |>
       show_scatter(alpha = 0.7, 
                    axes = FALSE, 
                    size = 2)

DEMO

Manual/radial tour

Best projection provided by the guided tour, separating three species.

Removing flipper length

Removing bill length

Games: Hiding in high-d

• Now you see it
• Now you don’t

library(tidyverse)
library(tourr)
library(GGally)
set.seed(946)
d <- tibble(x1=runif(200, -1, 1), 
            x2=runif(200, -1, 1), 
            x3=runif(200, -1, 1))
d <- d %>%
  mutate(x4 = x3 + runif(200, -0.1, 0.1))
d <- bind_rows(d, c(x1=0, x2=0, x3=-0.5, x4=0.5))

d_r <- d %>%
  mutate(x1 = cos(pi/6)*x1 + sin(pi/6)*x3,
         x3 = -sin(pi/6)*x1 + cos(pi/6)*x3,
         x2 = cos(pi/6)*x2 + sin(pi/6)*x4,
         x4 = -sin(pi/6)*x2 + cos(pi/6)*x4)

library(tidyverse)
library(tourr)
library(GGally)
set.seed(946)
d <- tibble(x1=runif(200, -1, 1), 
            x2=runif(200, -1, 1), 
            x3=runif(200, -1, 1))
d <- d %>%
  mutate(x4 = x3 + runif(200, -0.1, 0.1))
d <- bind_rows(d, c(x1=0, x2=0, x3=-0.5, x4=0.5))

d_r <- d %>%
  mutate(x1 = cos(pi/6)*x1 + sin(pi/6)*x3,
         x3 = -sin(pi/6)*x1 + cos(pi/6)*x3,
         x2 = cos(pi/6)*x2 + sin(pi/6)*x4,
         x4 = -sin(pi/6)*x2 + cos(pi/6)*x4)

Philosophy: Model in the data space

For example, when we teach regression, we overlay the fitted model on the data: MODEL IN THE DATA SPACE.

A residual plot is DATA IN THE MODEL SPACE. When we go beyond 2D, it’s considered too hard to show the model in the data space. It isn’t!

Wickham et al (2015) https://doi.org/10.1002/sam.11271

Dimension reduction

• Data in the model space
• PCA
• tSNE
• Oddness

Principal component analysis

NLDR: t-Stochastic neighbourhood embedding

Data in the model space

Model in the data space

library(mulgar)

p_pca_m <- pca_model(p_pca, s=2.2)
p_pca_m_d <- rbind(p_pca_m$points, penguins_sub[,1:4])
p_pca_m_d_clr <- c(rep("#EC5C00", 4), 
                   rep("black", nrow(penguins_sub)))
animate_xy(p_pca_m_d, edges=p_pca_m$edges,
           axes="bottomleft",
           col=p_pca_m_d_clr,
           edges.col="#EC5C00",
           edges.width=3)
render_gif(p_pca_m_d, 
           grand_tour(), 
           display_xy(half_range=4.2,
                      col=p_pca_m_d_clr,
                      edges=p_pca_m$edges, 
                      edges.col="#EC5C00",
                      edges.width=3),
           gif_file="gifs/p_pca_model.gif",
           frames=500,
           width=400,
           height=400,
           loop=FALSE)

Data in the model space

Model in the data space

https://doi.org/10.48550/arXiv.2506.22051

Exploring boundaries

The slice tour is especially useful for exploring classification models, comparing boundaries produced by different models. (The same penguins data used here.)

• Slice tour
• Static plots

Linear discriminant analysis

Classification tree

Linear discriminant analysis

Classification tree

Understanding clustering (1/2)

• Model-based
• Which is best?

Best model: four-cluster VEE

Three-cluster EEE

Understanding clustering (2/2)

Interactivity: Compare cluster models

DEMO

DATA 1: projections

$$\begin{eqnarray*} Y_{~n\times d} = XA = \left[ \begin{array}{cccc} y_{~11} & y_{~12} & \dots & y_{~1d} \\ y_{~21} & y_{~22} & \dots & y_{~2d}\\ \vdots & \vdots & & \vdots \\ y_{~n1} & y_{~n2} & \dots & y_{~nd} \end{array} \right]_{~n\times d} \end{eqnarray*}$$

DATA 2: cluster labels

$$\begin{eqnarray*} C = \left[ \begin{array}{cc} c_{~11} & c_{~12} \\ c_{~21} & c_{~22} \\ \vdots & \vdots \\ c_{~n1} & c_{~n2} \end{array} \right]_{~n\times 2} \end{eqnarray*}$$

library(crosstalk)
library(plotly)
library(viridis)
p_cl_shared <- SharedData$new(penguins_cl)

detour_plot <- detour(p_cl_shared, tour_aes(
  projection = bl:bm,
  colour = cl_w)) |>
    tour_path(grand_tour(2), 
                    max_bases=50, fps = 60) |>
       show_scatter(alpha = 0.7, axes = FALSE,
                    width = "100%", height = "450px")

conf_mat <- plot_ly(p_cl_shared, 
                    x = ~cl_mc_j,
                    y = ~cl_w_j,
                    color = ~cl_w,
                    colors = viridis_pal(option = "D")(3),
                    height = 450) |>
  highlight(on = "plotly_selected", 
              off = "plotly_doubleclick") %>%
    add_trace(type = "scatter", 
              mode = "markers")
  
bscols(
     detour_plot, conf_mat,
     widths = c(5, 6)
 )                 

Departures from normal

• Normal?
• Longitudinal

Liver function (6D) among a sample of patients (all women).

Liver function (6D) among a sample of aging patients patients.

See Calvi, Laa, Cook (2025)

Deconstructing neural networks

• Data
• NN Model
• Two PCs
• Five PCs

Example: MNIST fashion

10 fashion items, 60000 training 28x28 images

Model fitted as described in keras tutorial.

Single hidden layer with 128 nodes, which reduces the 28x28= 784-dimensional space to 128-dimensional space.

What does this dimension reduction do for the classification?

Principal components is the usual way to manage constructing a smaller number of dimensions to view the data.

Feedforward back-propagation model

Input space

Activations

High-dimensional ternary diagrams

If you have more than three components in a compositional data set, the data falls inside a simplex, of more than 2D.

• 2D
• High-d

Each component forms one vertex of the simplex. Points

• at vertices are certain predictions
• far from their vertex are uncertain, likely confused
• along an edge are confused between two groups only
• along a face are confused between three groups

Helps to understand uncertainty in predictions more than is possible with a confusion matrix.

Summary

The tourr package provides the algorithm to generate the tour paths of projection bases, and also the ability to create new tours, and draw projections with a variety of different display methods.

Tours provide the ability to do statistics with visual help.

These paths of projections can be generated off-line and used with other software.

Elegant interactivity solutions with detourr, liminal, langevitour, lionfish but need to be developed further.

High-d vis intellectually challenging, and fun!

Please use these tools 😃

References and acknowledgements

• Cook and Laa (2023) Interactively exploring high-dimensional data and models in R
• Wickham et al (2015) Visualizing statistical models: Removing the blindfold
• Flatland: A Romance of Many Dimensions (1884) Edwin Abbott
• R packages: tourr, woylier, detourr, liminal, langevitour, lionfish, geozoo.

Slides made in Quarto, with code included.

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.