Creating data plots for effective decision-making using statistical inference with R

Dianne Cook
Monash University

Session 2: Making decisions and inferential statements based on data plots

Outline

time	topic
3:00-3:20	What is your plot testing?
3:20-3:35	Creating null samples
3:35-4:00	Conducting a lineup test
4:00-4:30	Testing for best plot design

What is your plot testing? (1/3)

LM_FIT <- lm(VAR2 ~ VAR1, 
             data = DATA)
FIT_ALL <- augment(LM_FIT)
ggplot(FIT_ALL, aes(x=.FITTED, 
                    y=.RESID)) + 
  geom_point()

What will we be assessing using this plot?

Is the model misspecified?

non-linearity
heteroskedasticity
outliers/anomalies
non-normality
fitted value distribution

What is your plot testing? (1/3)

What do you see?

✗ non-linearity
✓ heteroskedasticity
✗ outliers/anomalies
✓ non-normality
✗ fitted value distribution is uniform

Are you sure?

What is your plot testing? (2/3)

ggplot(DATA, 
       aes(x=VAR1, 
           y=VAR2, 
           color=CLASS)) + 
  geom_point()

What will we be assessing using this plot?

Is there a difference between the groups?

location
shape
outliers/anomalies

What is your plot testing? (2/3)

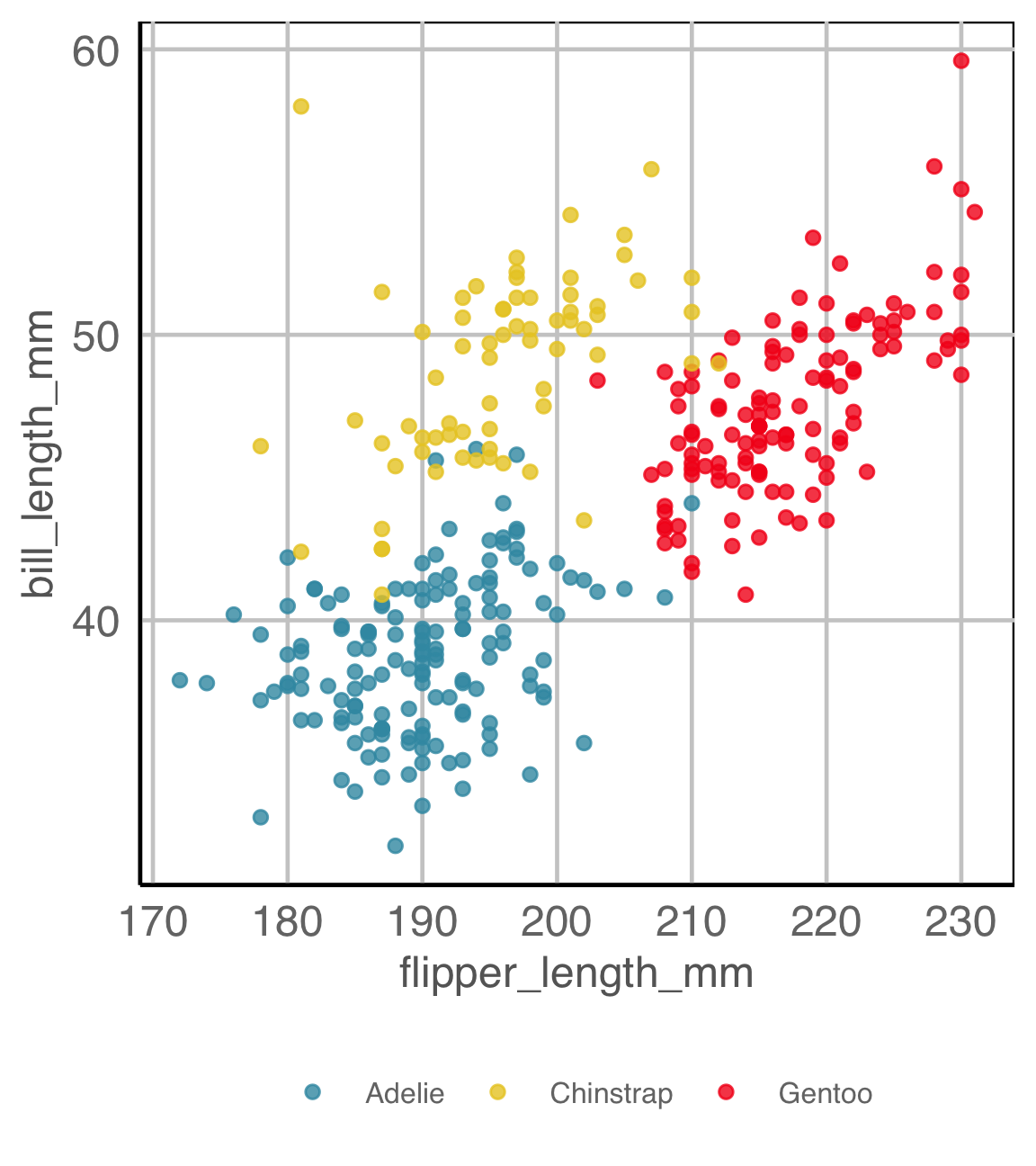
What do you see?

There a difference between the groups

✓ location
✗ shape
✓ outliers/anomalies

Are you sure?

What is your plot testing? (3/3)

ggplot() + 
  geom_tile(DATA, 
    aes(x=LONGITUDE, 
        y=LATITUDE, 
        fill=VAR1)) +
  geom_path(MAP, 
        aes(x=LONGITUDE, 
            y=LATITUDE,
            group=GROUP)) +
  theme_map()

What will we be assessing using this plot?

Is there a spatial trend?

Are there any spatial anomalies?

What is your plot testing? (3/3)

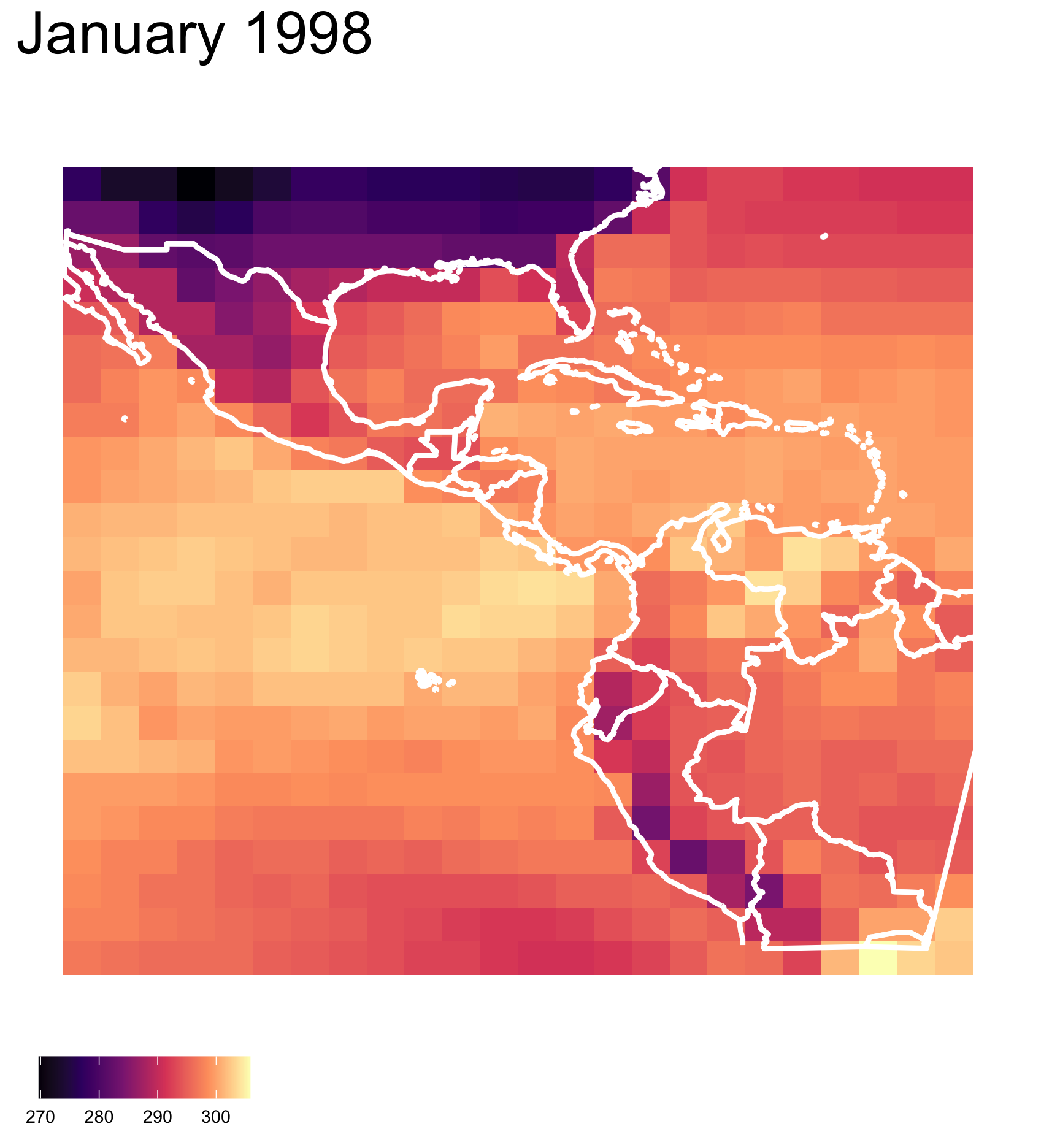
What do you see?

There are clusters of high and low temperature in different parts of the region.

✓ clusters
✓ outliers/anomalies

Are you sure?

Statistical thinking

Because the plot is specified using a functional mapping of the variables, it is a statistic.
The null and alternative hypotheses are indicated from the plot description.
Applying the function to a dataset provides the observed value.

Null hypothesis, example 1

LM_FIT <- lm(VAR2 ~ VAR1, 
             data = DATA)
FIT_ALL <- augment(LM_FIT)
ggplot(FIT_ALL, aes(x=.FITTED, 
                    y=.RESID)) + 
  geom_point()

What is the null hypothesis?

There is no relationship between residuals and fitted values. This is \(H_o\).

Alternative hypothesis, \(H_a\):

There is some relationship, which might be

non-linearity
heteroskedasticity
outliers/anomalies

Null hypothesis, example 2

ggplot(DATA, 
       aes(x=VAR1, 
           y=VAR2, 
           color=CLASS)) + 
  geom_point()

What is the null hypothesis?

There is no difference between the classes. This is \(H_o\).

Alternative hypothesis, \(H_a\):

There is some difference between the classes, which might be

location
shape
outliers/anomalies

Exercise

What is being tested in each of these plot descriptions?

ggplot(DATA, 
       aes(x=VAR1)) +
  geom_histogram()

ggplot(DATA, 
       aes(x=VAR1, 
           fill=VAR2)) +
  geom_bar(position="fill")

ggplot(DATA, 
       aes(x=VAR1, 
           y=VAR2)) +
  geom_point() +
  geom_smooth()

Distribution of VAR1 is ?

There is no relationship between VAR1 and VAR2. More specifically, the proportion of VAR2 in each level of VAR1 is the same.

There is no relationship between VAR1 and VAR2. Particularly, VAR2 is not dependent on VAR1 and there is no trend.

Creating null samples

Statistical thinking

Sampling distribution for a t-statistic. Values expected assuming \(H_o\) is true. Shaded areas indicate extreme values.

For making comparisons when plotting, draw a number of null samples, and plot them with the same script in the plot description.

Creating null samples, example 1

ggplot(DATA, 
       aes(x=VAR1, 
           y=VAR2, 
           color=CLASS)) + 
  geom_point()

\(H_o\): There is no difference between the classes.

How would you generate null samples?

Break any association by permuting (scrambling/shuffling/re-sampling) the CLASS variable.

Creating null samples, example 2

LM_FIT <- lm(VAR2 ~ VAR1, 
             data = DATA)
FIT_ALL <- augment(LM_FIT)
ggplot(FIT_ALL, aes(x=.FITTED, 
                    y=.RESID)) + 
  geom_point()

\(H_o\): There is no relationship between residuals and fitted values.

How would you generate null samples?

Break any association by

permuting residuals,
or residual rotation,
or simulate residuals from a normal distribution.

Conducting a lineup test

Steps

Create a lineup of \(m-1\) null plots + 1 data plot, where the data plot is randomly placed among nulls. Remove any distracting information, like tick labels, titles.
Ask uninvolved observer(s) to pick the plot that is most different. (May need to use a crowd-sourcing service.)
Compute the probability that the data plot was chosen, assuming it is no different from the null plots. This is the \(p\)-value.
Decide to reject or fail to reject the null.

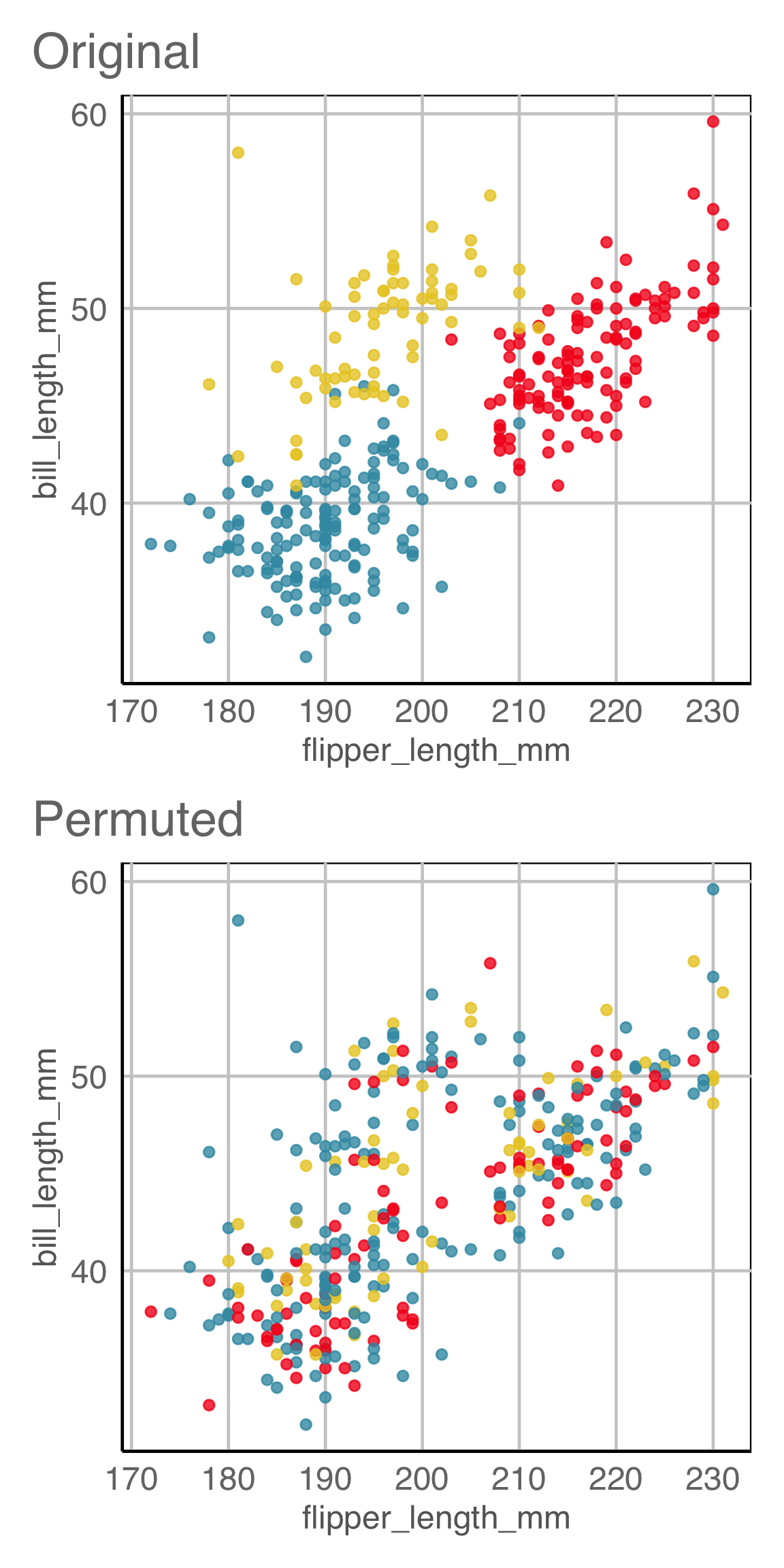
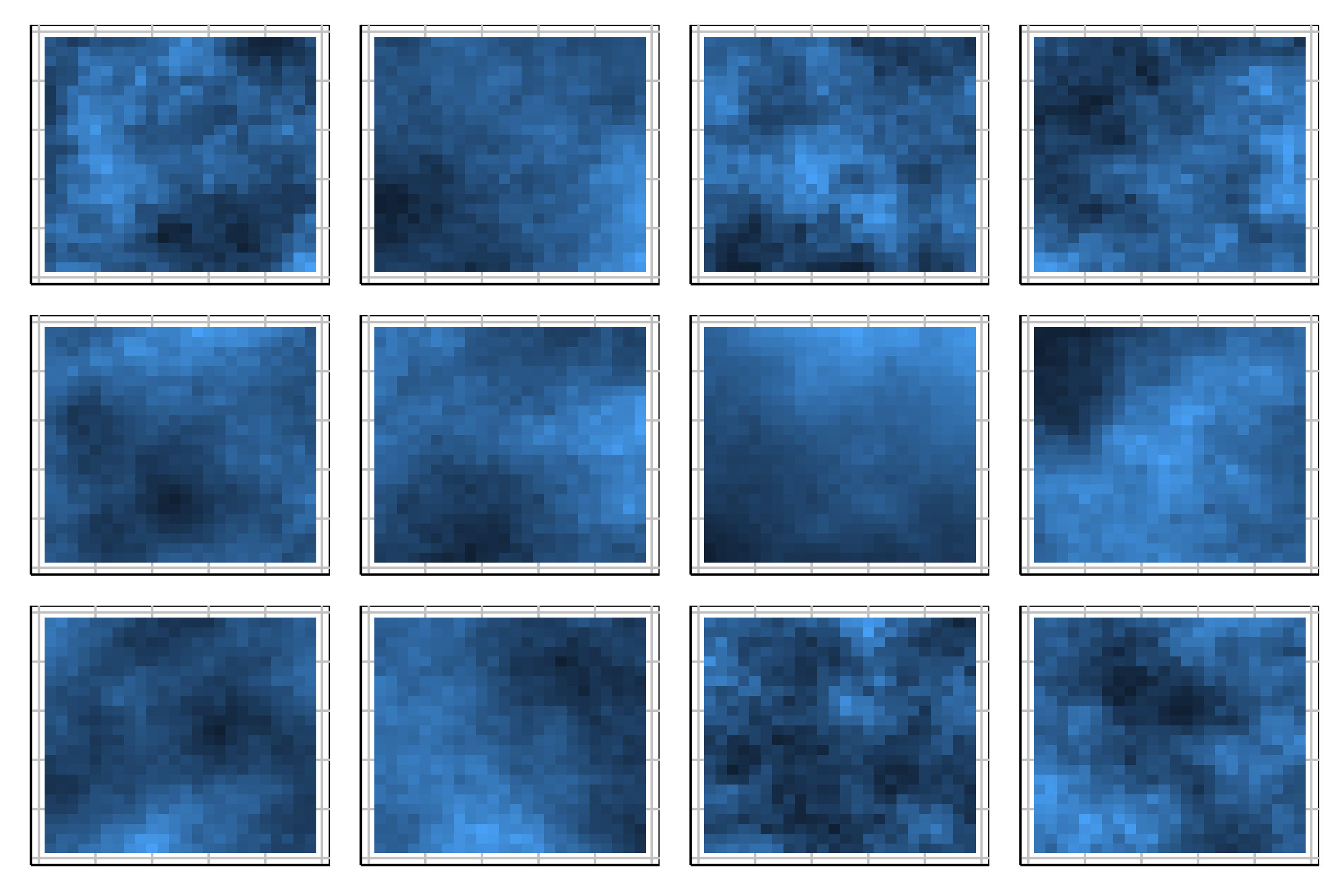
Lineup example 1 (1/2)

Code

set.seed(241)
ggplot(lineup(null_permute("species"), penguins, n=15), 
       aes(x=flipper_length_mm, 
           y=bill_length_mm, 
           color=species)) + 
  geom_point(alpha=0.8) +
  facet_wrap(~.sample, ncol=5) +
  scale_color_discrete_divergingx(palette="Zissou 1") +
  theme(legend.position = "none",
        axis.title = element_blank(),
        axis.text = element_blank(),
        panel.grid.major = element_blank())

Lineup example 1 (2/2)

If 10 people are shown this lineup and all 10 pick plot 2, which is the data plot, the \(p\)-value will be 0.

Generally, we can compute the probability that the data plot is chosen by \(x\) out of \(K\) observers, shown a lineup of \(m\) plots, using a simulation approach that extends from a binomial distribution, with \(p=1/m\).

pvisual(10, 10, 15)

      x simulated        binom
[1,] 10         0 1.734168e-12

This means we would reject \(H_o\) and conclude that there is a difference in the distribution of bill length and flipper length between the species of penguins.

Lineup example 2 (1/2)

Code

data(wasps)
set.seed(258)
wasps_l <- lineup(null_permute("Group"), wasps[,-1], n=15)
wasps_l <- wasps_l |>
  mutate(LD1 = NA, LD2 = NA)
for (i in unique(wasps_l$.sample)) {
  x <- filter(wasps_l, .sample == i)
  xlda <- MASS::lda(Group~., data=x[,1:42])
  xp <- MASS:::predict.lda(xlda, x, dimen=2)$x
  wasps_l$LD1[wasps_l$.sample == i] <- xp[,1]
  wasps_l$LD2[wasps_l$.sample == i] <- xp[,2]
}
ggplot(wasps_l, 
       aes(x=LD1, 
           y=LD2, 
           color=Group)) + 
  geom_point(alpha=0.8) +
  facet_wrap(~.sample, ncol=5) +
  scale_color_discrete_divergingx(palette="Zissou 1") +
  theme(legend.position = "none",
        axis.title = element_blank(),
        axis.text = element_blank(),
        panel.grid.major = element_blank())

Lineup example 2 (2/2)

If 10 people are shown this lineup and 1 picked the data plot (position 6), which is the data plot, the \(p\)-value will be large.

pvisual(1, 10, 15)

     x simulated     binom
[1,] 1    0.4639 0.4983882

This means we would NOT reject \(H_o\) and conclude that there is NO difference in the distribution of groups.

What is the \(p\)-value?

Suppose \(X\) is the number of heads out of \(n\) independent tosses.
Let \(p\) be the probability of getting a for this coin.
Hypotheses: \(H_0: p = 0.5\) vs. \(H_a: p > 0.5\).
Alternative \(H_a\) is saying we believe that the coin is biased to heads.
Alternative needs to be decided before seeing data.
Assumption: Each toss is independent with equal chance of getting a head.

What is the \(p\)-value?

Suppose I have a coin that I’m going to flip
Experiment 1: I flipped the coin 10 times and this is the result:

The result is 7 heads and 3 tails. So 70% are heads.
Do you believe the coin is biased based on this data?

What is the \(p\)-value?

Experiment 2: Suppose now I flip the coin 100 times and this is the outcome:

We observe 70 heads and 30 tails. So again 70% are heads.
Based on this data, do you think the coin is biased?

Calculate the \(p\)-value

Experiment 1 (n=10)

We observed \(x=7\), or \(\widehat{p} = 0.7\).
Assuming \(H_0\) is true, we expect \(np=10\times 0.5=5\).
Calculate the \(P(X \geq 7)\)

sum(dbinom(7:10, 10, 0.5))

[1] 0.171875

Experiment 2 (n=100)

We observed \(x=70\), or \(\widehat{p} = 0.7\).
Assuming \(H_0\) is true, we expect \(np=100\times 0.5=50\).
Calculate the \(P(X \geq 70)\)

sum(dbinom(70:100, 100, 0.5))

[1] 3.92507e-05

Lineup \(p\)-value and power

Suppose \(x\) out of \(n\) people detected the data plot from a lineup, then the visual inference p-value is given as \(P(X \geq x)\) where \(X \sim B(n, 1/m)\), but

the assumption of independence is not strictly satisfied, if people are shown the same lineup. So the \(p\)-value is computed by simulation with

nullabor::pvisual()

and the power of a lineup is estimated as \(x/n\). We’ll use this to compare the signal strengths for different plot designs. Stay tuned!

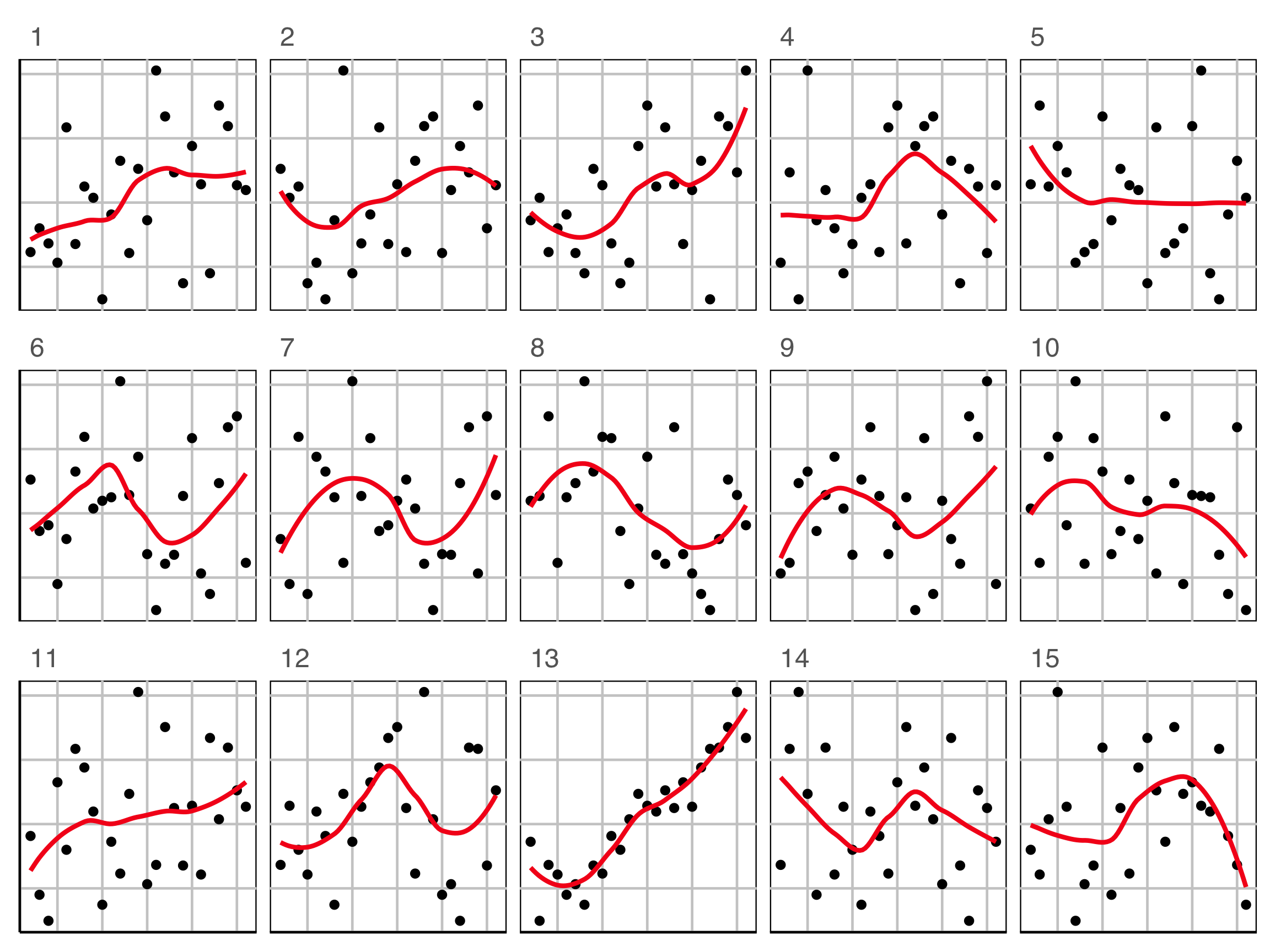
Lineup example 3 (1/2)

Which plot is the most different?

Lineup example 3 (2/2)

Plot description was:

ggplot(stars, aes(x=temp)) +
  geom_density()

In particular, the researcher is interested to know if star temperature is a skewed distribution.

\(H_o: X\sim exp(\widehat{\lambda})\)
\(H_a:\) it has a different distribution.

Generate the lineup with:

lineup(null_dist("temp", "exp", 
  list(rate = 1 / 
         mean(dslabs::stars$temp))), 
  stars, n=15)

Compute the \(p\)-value based on your responses to the lineup (previous slide).

pvisual(n=??, k=??, m=15)

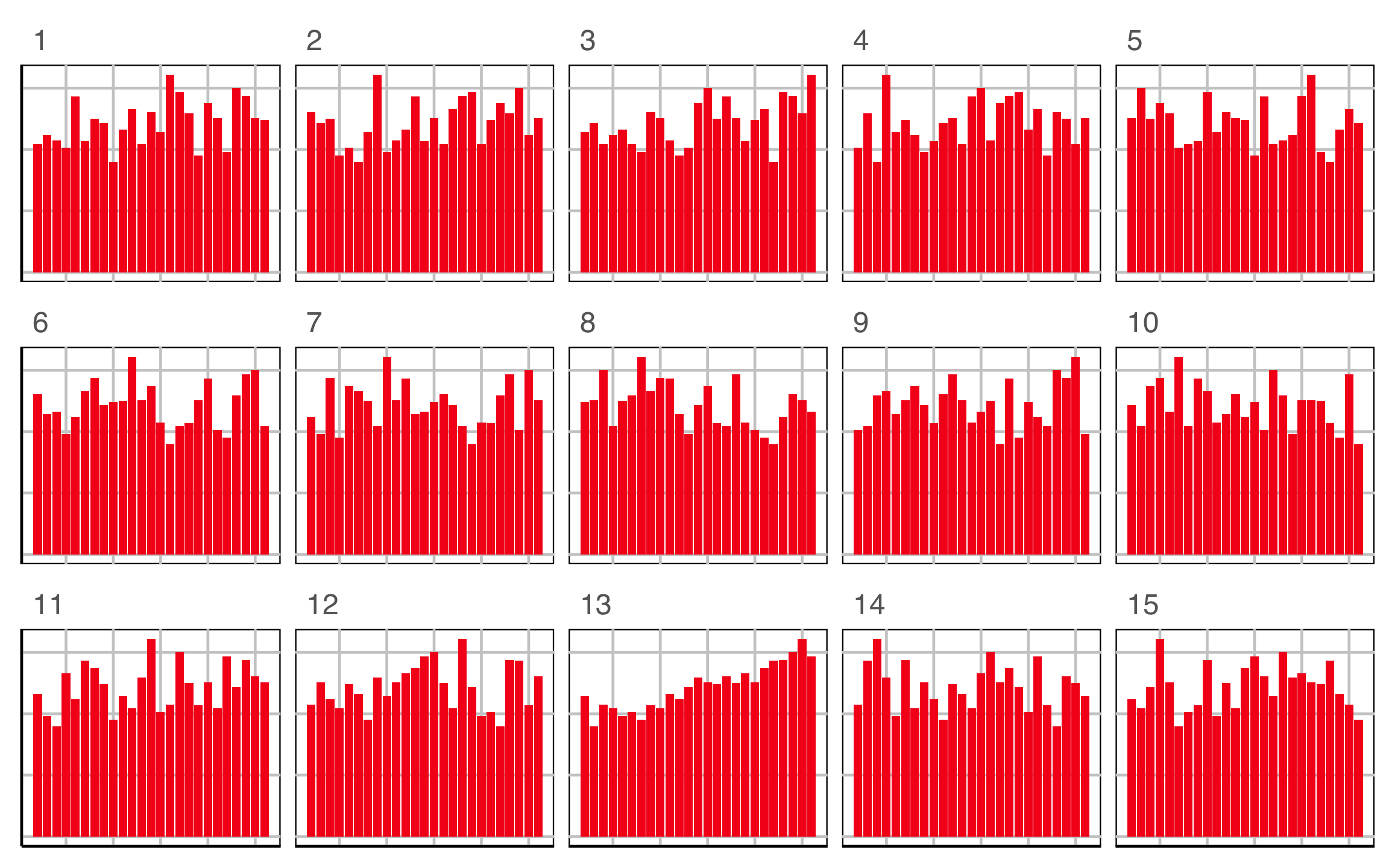
Lineup example 4 (1/2)

Which row of plots is the most different?

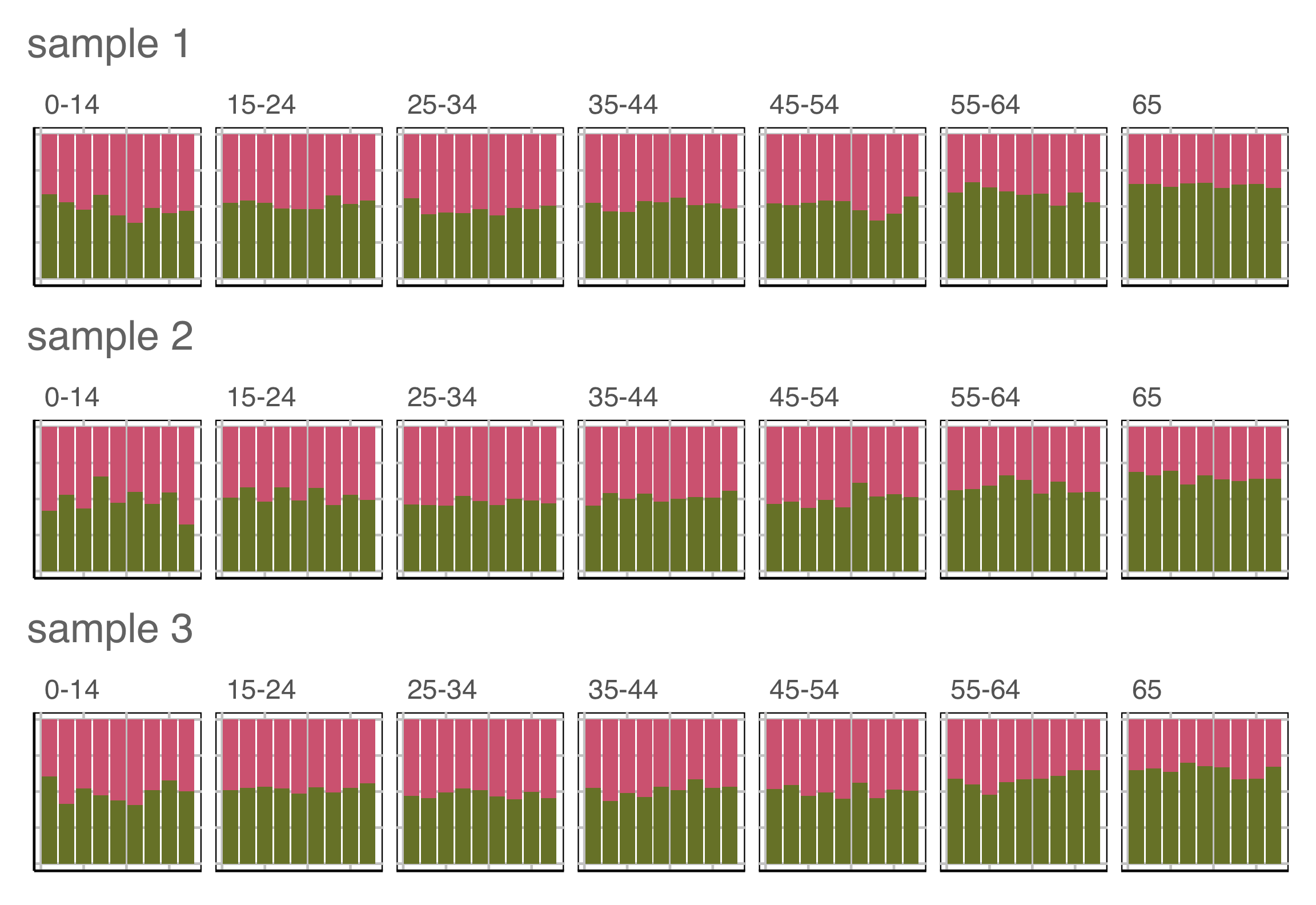
Lineup example 4 (2/2)

Plot description was:

ggplot(tb_aus_sa, 
       aes(x=year, 
           y=count, 
           fill=sex)) + 
  geom_col(position="fill") +
  facet_wrap(~age, ncol=7)

\(H_o:\) Proportion of males and females is the same for each year, conditional on age group
\(H_a:\) it’s not

Generate the lineup with:

b_aus_sa |> 
  uncount(count) |>
  group_by(age) |>
  mutate(sex = sample(sex, 
    replace = FALSE)) |>
  count(sex, age, year)

Compute the \(p\)-value based on your responses to the lineup (previous slide).

pvisual(n=??, k=??, m=3)

Practical considerations

Testing can be done informally with the nullabor package
For practical use, one should
- Create multiple lineups for a data plot, different positions, different nulls
- Show each to different groups of observers
- Compute \(p\)-value by combining results from each lineup.
Crowd-sourcing services include: Amazon Mechanical Turk, prolific, Appen, LABVANCED.

Exercise

Take a moment to look at the lineup function documentation. Run the sample code to make a lineup, eg:

ggplot(lineup(null_permute('mpg'), mtcars), aes(mpg, wt)) +
  geom_point() +
  facet_wrap(~ .sample)

or your own.

And then the different null sample generating functions: null_permute, null_lm, null_ts, null_dist.

Testing for best plot design

Steps

Decide on plot descriptions, say two possibilities.
Using the same data, and same null data create lineups that only differ because of the plot description.
Show each lineup to two samples of uninvolved observers (one observer cannot see both lineups).
Compute the proportion of each sample who identified the data plot, this is the signal strength or statistical power of each plot design.
The plot with the greater value is the best design (for that problem).

If your birthday is between Jan 1 and Jun 30, CLOSE YOUR EYES NOW

No peeking!

Which plot is the most different?

Raise your hand when you have chosen.

00:20

Blank
Plot design 1A
Plot design 1B

Plot design example 1

This is the pair of plot designs we are evaluating.

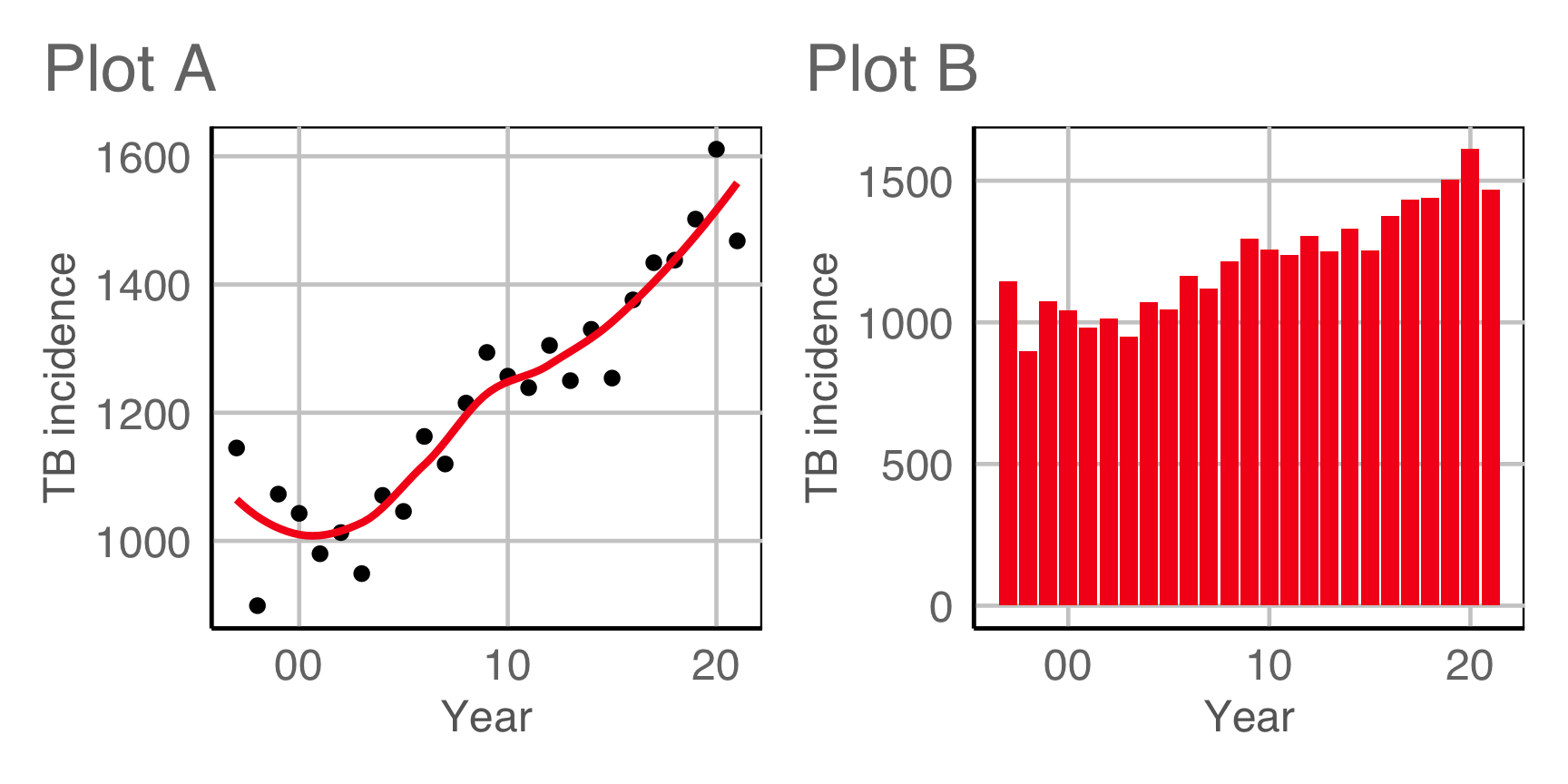
Compute signal strength:

?? / ??

If your birthday is between Jul 1 and Dec 31, CLOSE YOUR EYES NOW

No peeking!

Which plot is the most different?

Raise your hand when you have chosen.

00:20

Blank
Plot design 2A
Plot design 2B

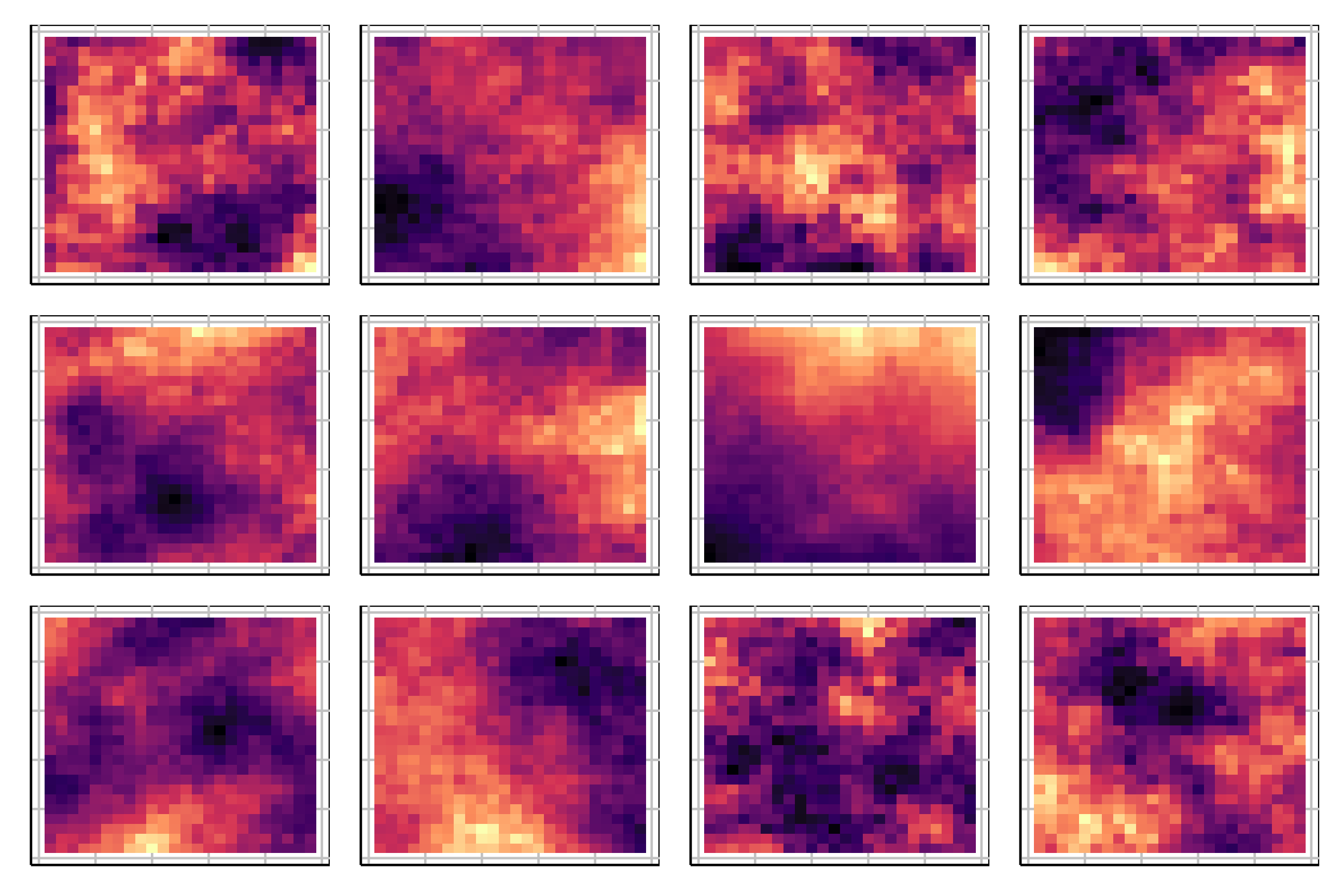
Plot design example 2

This is the pair of plot designs we are evaluating. Comparing colour palettes used for the spatial distribution of temperature.

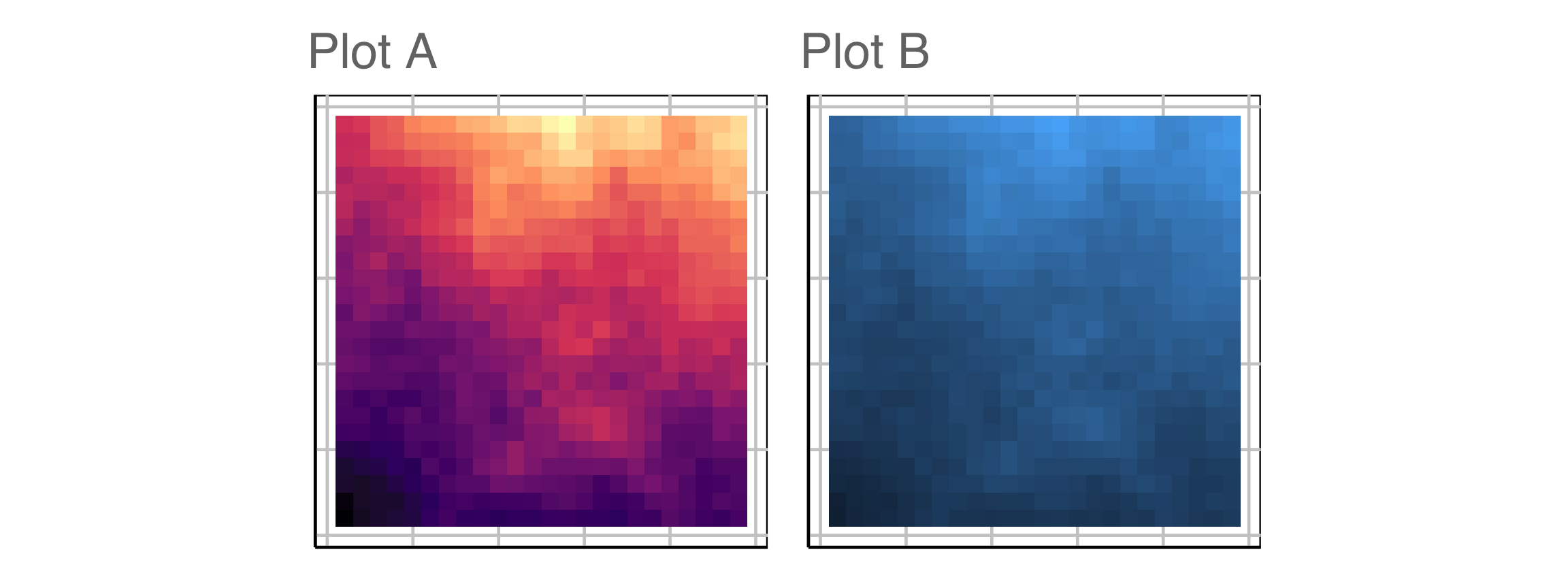
Compute signal strength:

?? / ??

Exercise

For the star temperature data, where we used this plot design

ggplot(stars, aes(x=temp)) +
  geom_density()

create a lineup with a different design, that you think might reveal the data distribution as different from null samples, better than the density plot. Possibilities could include geom_histogram, ggbeeswarm::quasirandom, lvplot::geom_lv.

Exercise

Choose one of your own plots, and decide on two choices in the design. Map out:

What it is testing
How to generate nulls
Make a lineup with each design

Take-aways

Think about what variability or associations your plot will be assessing
What would be not interesting pattern(s)
How would you generate data with where there is no interesting pattern
Plot samples of null data to understand what patterns occur by chance
With lineups you can compute the
- significance of a pattern
- strength of the signal in one type of display relative to another

Wrap up

To learn more

Wickham, Cook, Hofmann, Buja (2010) Graphical Inference for Infovis, IEEE TVCG, https://doi.org/10.1109/TVCG.2010.161.
Hofmann, Follett, Majumder, Cook (2012) Graphical Tests for Power Comparison of Competing Designs, IEEE TVCG, https://doi.org/10.1109/TVCG.2012.230.
Buja, Cook, Hofmann, Lawrence, Lee EK, Swayne, Wickham (2009) Statistical inference for exploratory data analysis and model diagnostics, https://doi.org/10.1098/rsta.2009.0120.
Majumder, Hofmann, Cook (2013) Validation of visual statistical inference, applied to linear models, https://doi.org/10.1080/01621459.2013.808157.
VanderPlas, Rottger, Cook, Hofmann (2021) Statistical significance calculations for scenarios in visual inference, https://doi.org/10.1002/sta4.337.

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.