Creating data plots for effective decision-making using statistical inference with R

Dianne Cook
Monash University

Session 1: Making effective plots using ggplot2’s grammar of graphics

Outline

time topic
1:30-1:45 Why, philosophy and benefits
1:45-2:05 Organising data to map variables to plots
2:05-2:35 Making a variety of plots
2:35-3:00 Do but don’t, and cognitive principles
3:00-3:30 BREAK

Why (1/6)

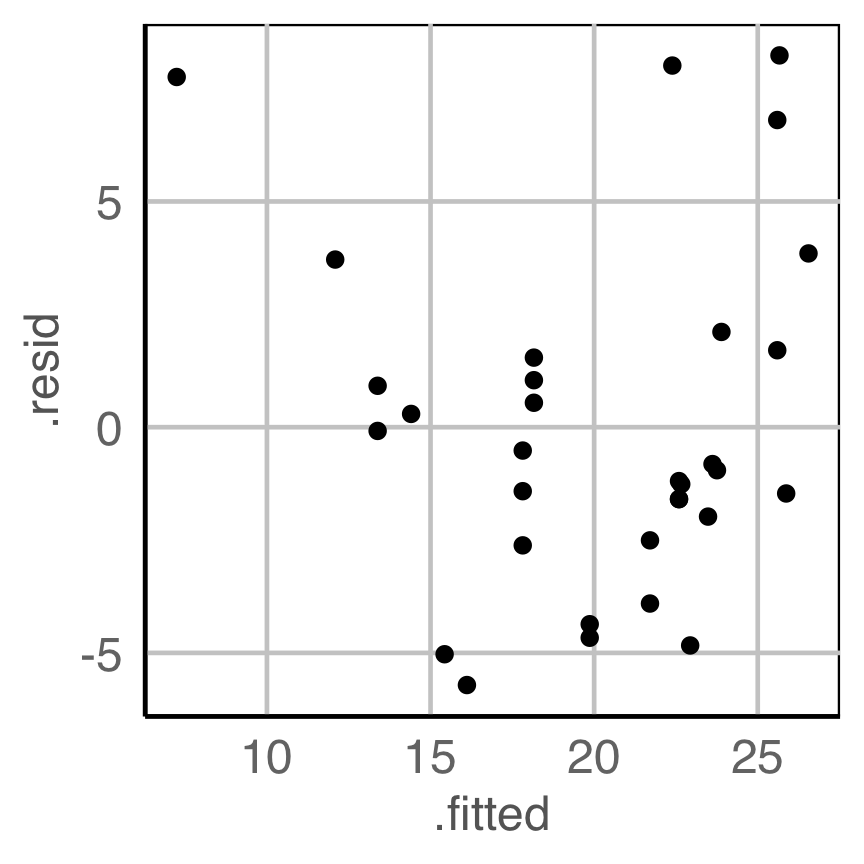
Is there any pattern in the residuals that indicate a problem with the model fit?


Do we need to change the model specification?

Why (2/6)



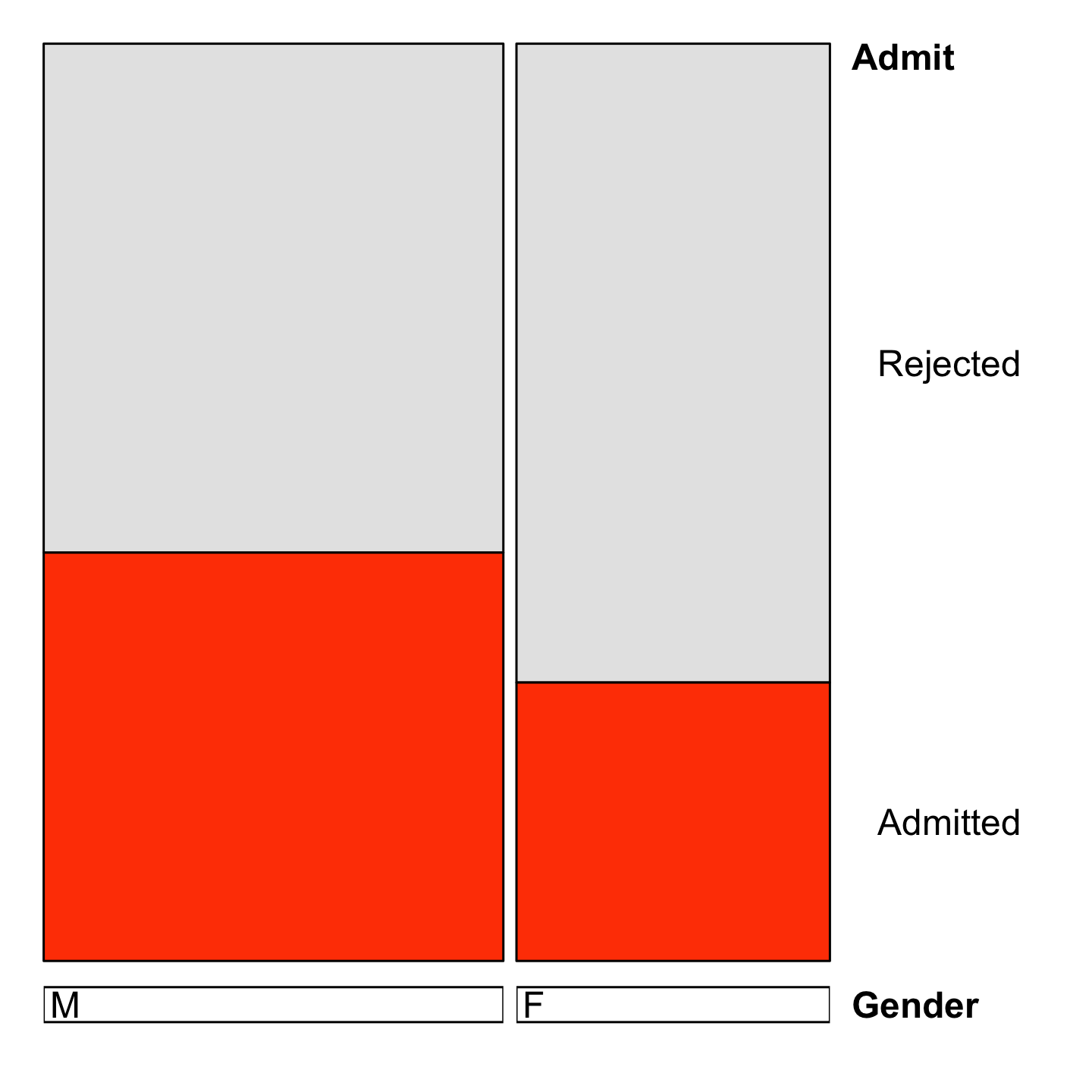
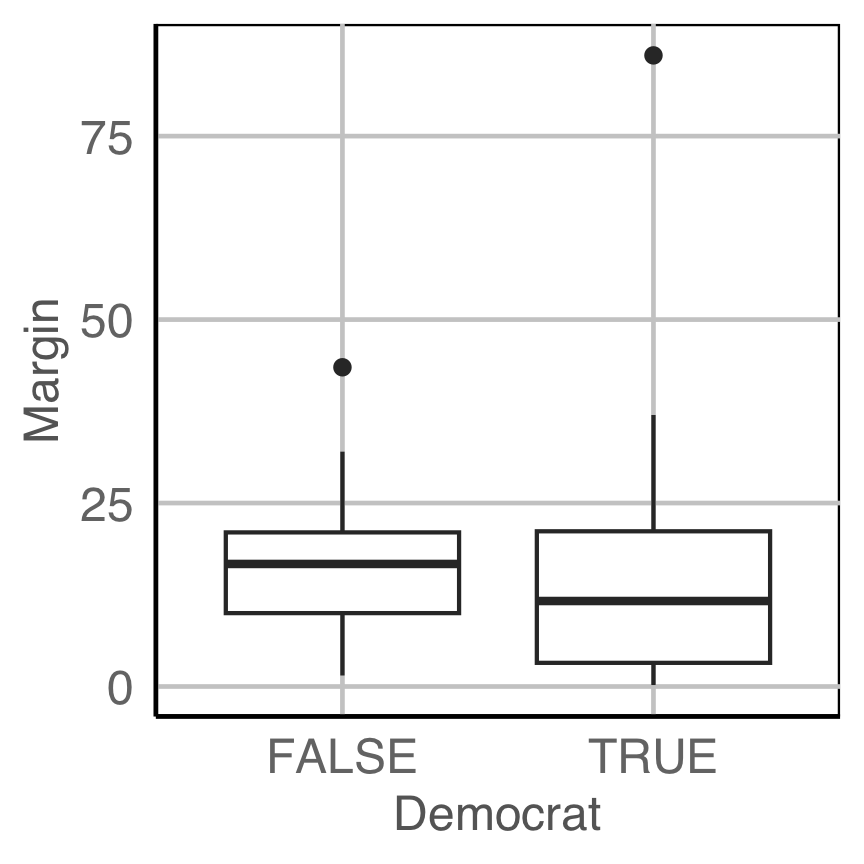
Is there a bias in admissions?

Why (3/6)


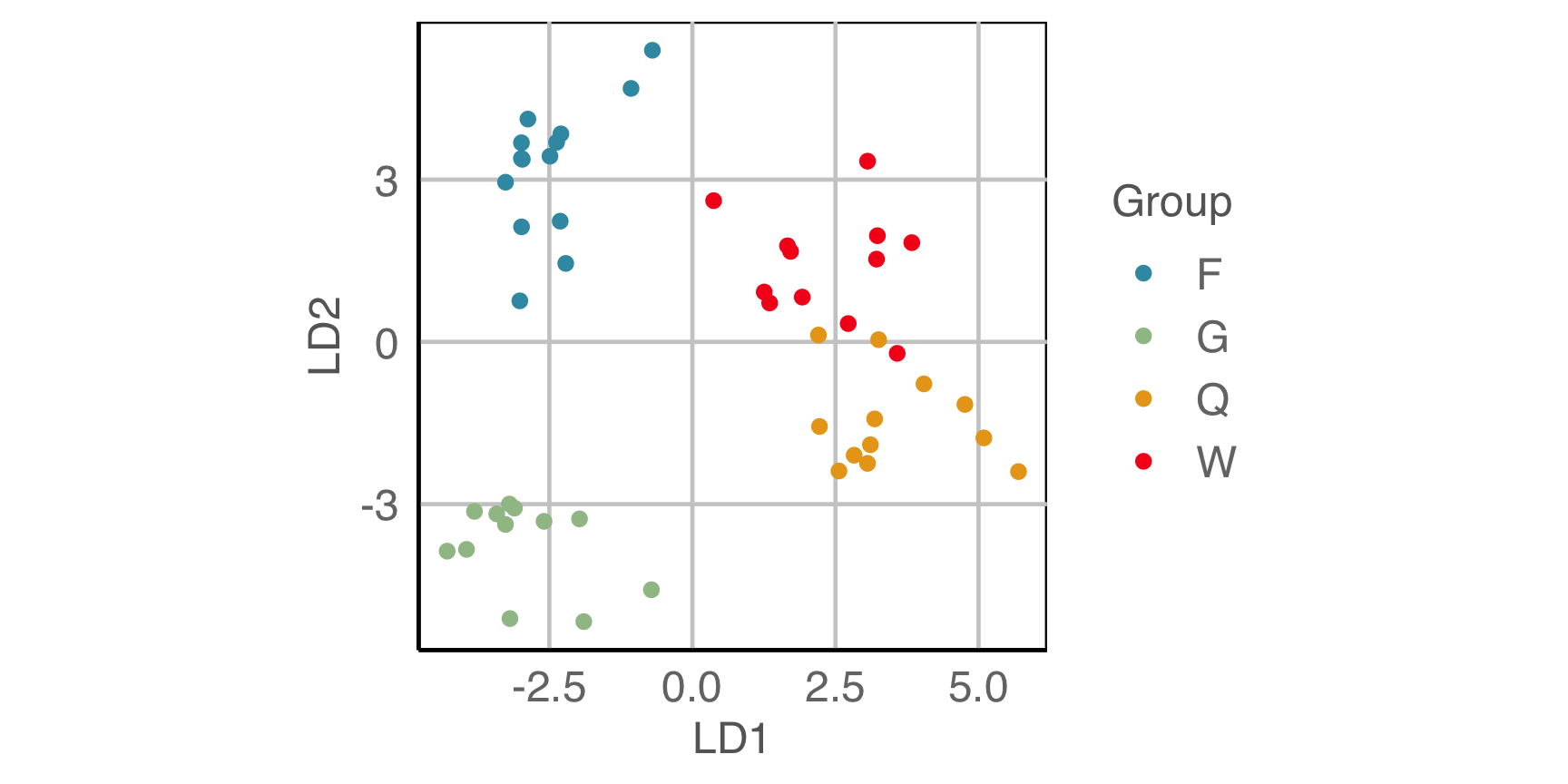
Is there a difference between the species?

Why (4/6)


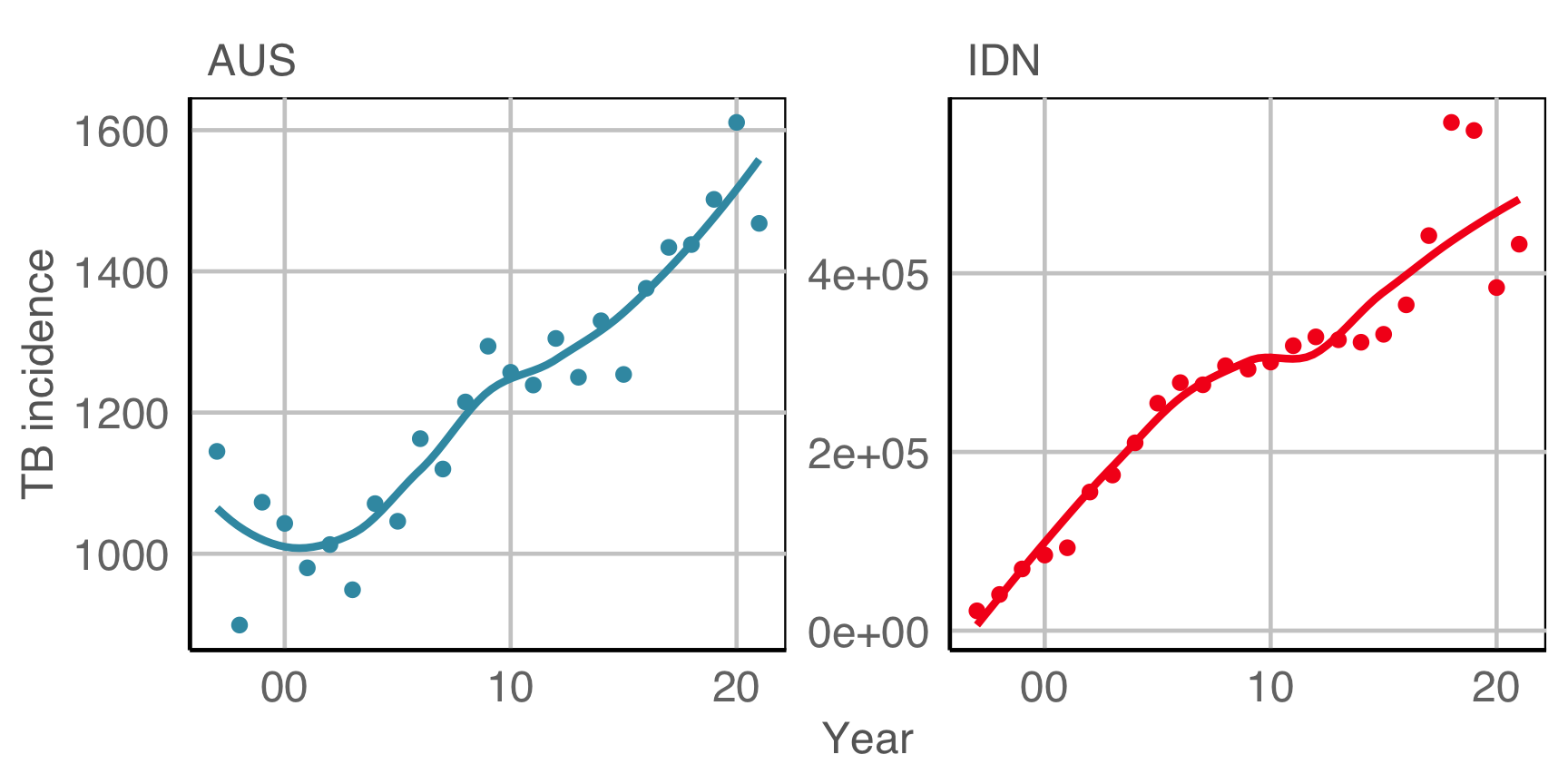
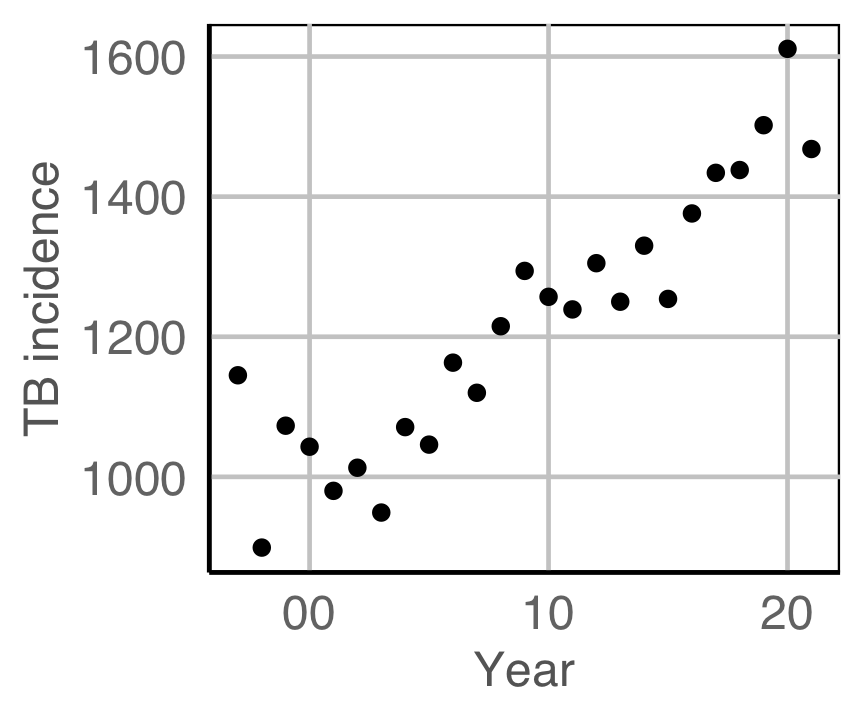
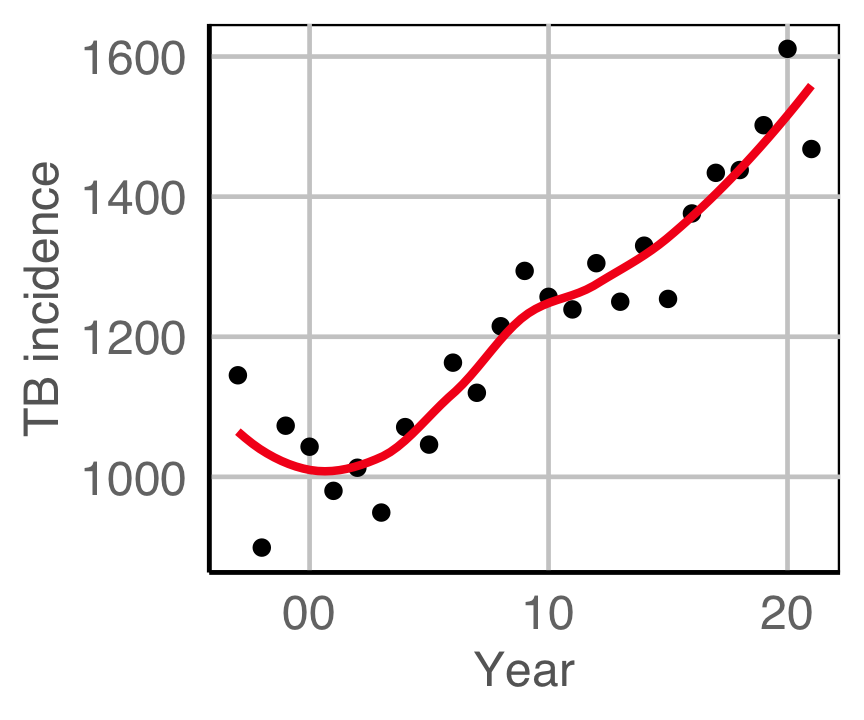
Is TB getting worse? (In Australia and Indonesia)

(From the World Health Organisation (WHO)]

Why (5/6)


Which is the best display to answer the previous question?

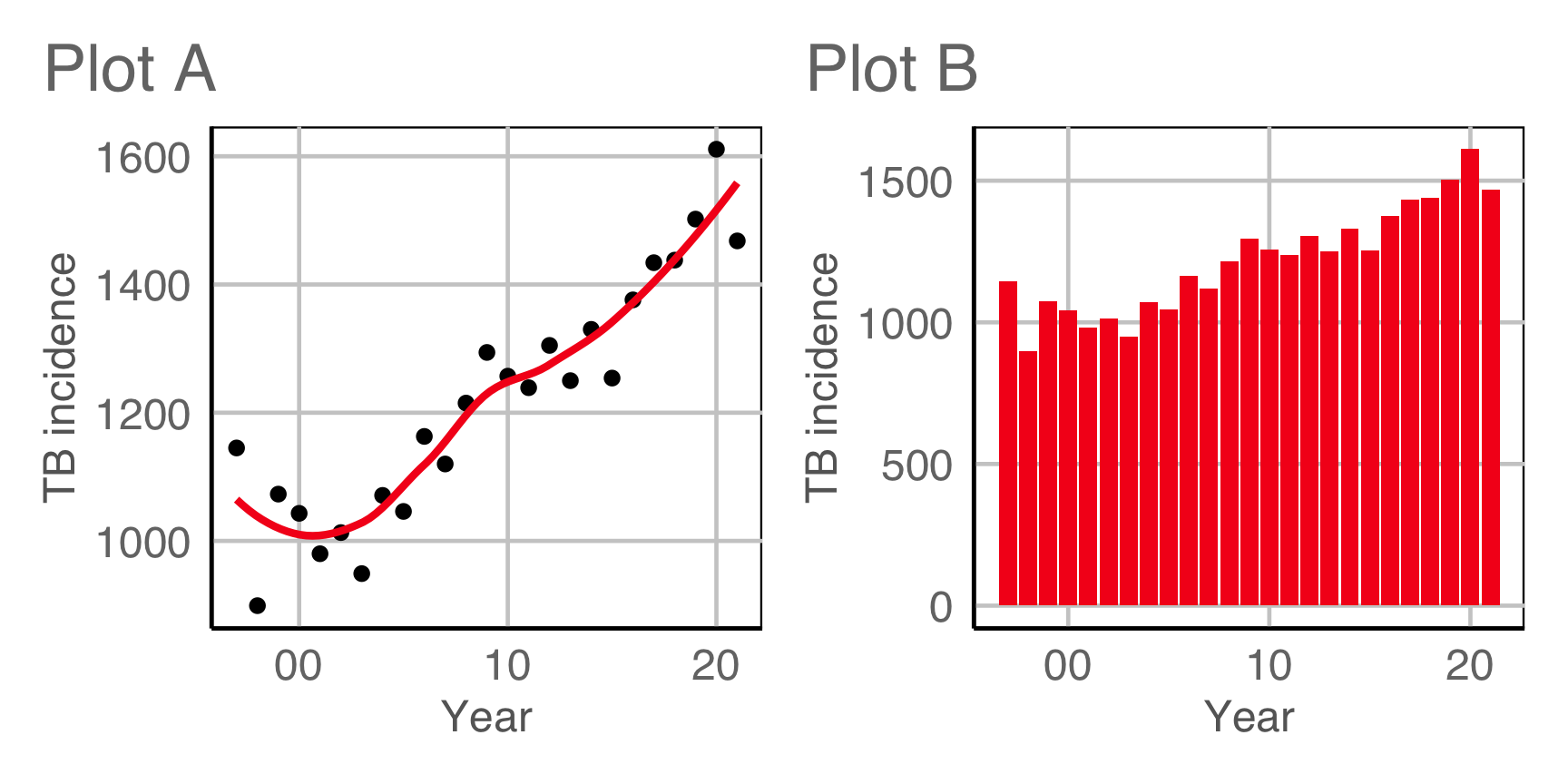
Why (6/6)


Which is the best display to answer: what is distribution of thyroid cancer across Australia?

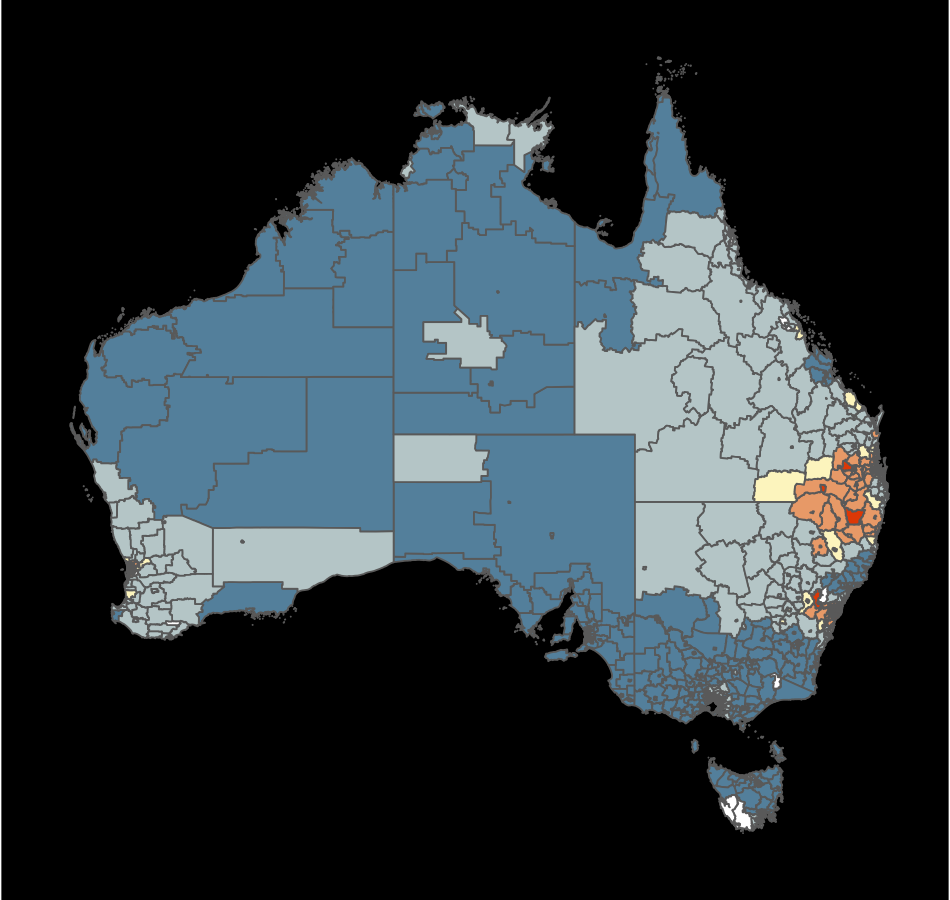
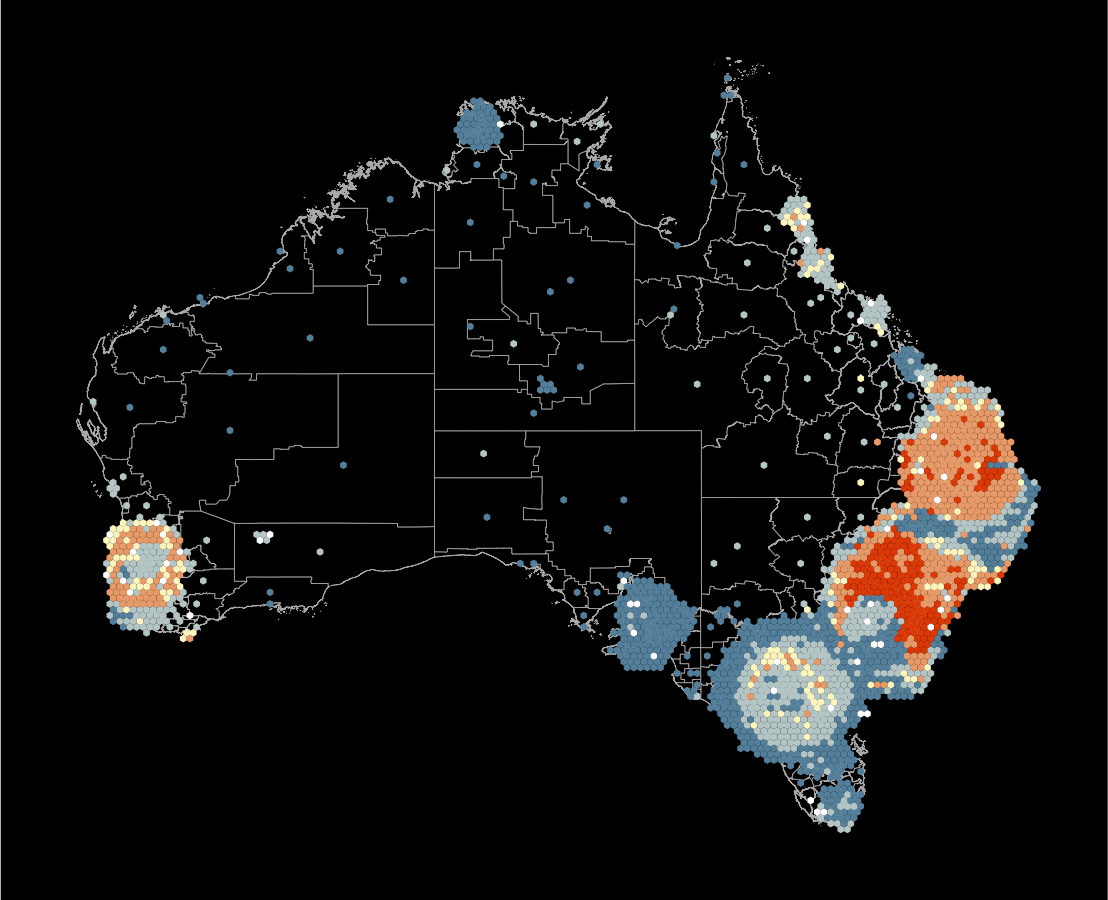
What’s the goal?


Reading data plots is subjective.


Making decisions based on data visualisations is common, where we need to be objective .




It is possible, and here is how we do that …

These are the tools you need

install.packages("ggplot2")

or better yet:

install.packages("tidyverse")
  • Define your plots using a grammar that maps variables in tidy data to elements of the plot.
  • Wrangle your data into tidy form for clarity of plot specification.

space 

install.packages("nullabor")
  • Compare your data plot to plots of null data.
  • This checks whether what we see is real or spurious.
  • Also allows for measuring the effectiveness of one plot design vs another.

Organising your data to enable mapping variables to graphical elements

Tidy data





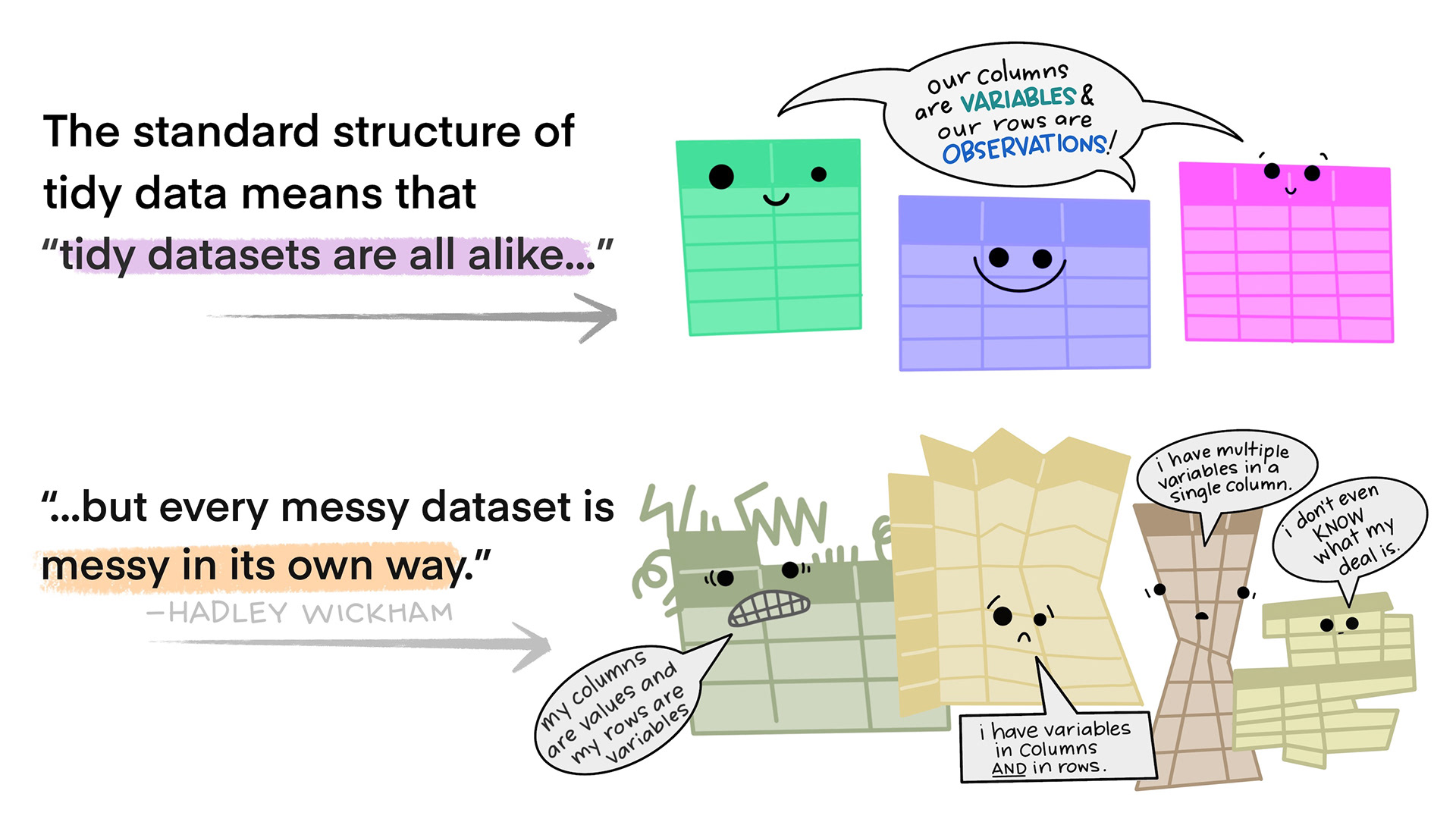
  1. Each variable forms a column
  2. Each observation forms a row
  3. Each type of observational unit forms a table. If you have data on multiple levels (e.g. data about houses and data about the rooms within those houses), these should be in separate tables.

Illustrations from the Openscapes blog Tidy Data for reproducibility, efficiency, and collaboration by Julia Lowndes and Allison Horst

YOUR TURN

For each of the following data discuss whether it is in tidy form.

Data 1: tuberculosis from WHO

Data 2: Graduate programs

Data 3: GHCN weather station records

Answers

Data 1:
Not in tidy form

  • iso3
  • year
  • gender
  • age

Data 2:
It’s in tidy form!

  • subject
  • inst
  • AvNumPubs
  • AvNumCits
  • …

Data 3:
Not in tidy form

  • station
  • year
  • month
  • day
  • TMAX
  • TMIN
  • PRCP

Statistical data

\[X = \left[ \begin{array}{rrrr} X_{~1} & X_{~2} & ... & X_{~p} \end{array} \right] \\ = \left[ \begin{array}{rrrr} X_{~11} & X_{~12} & ... & X_{~1p} \\ X_{~21} & X_{~22} & ... & X_{~2p} \\ \vdots & \vdots & \ddots& \vdots \\ X_{~n1} & X_{~n2} & ... & X_{~np} \end{array} \right]\]

  • This is tidy data!
  • You might also make assumptions about the distribution of each variable, e.g. \(X_{~1} \sim N(0,1), ~~X_{~2} \sim \text{Exp}(1) ...\)

Mapping

In ggplot2, the variables from tidy data are explicitly mapped to elements of the plot, using aesthetics.

Basic Mappings

  • x and y to plot points in a two-dimensional space
  • color, fill to render as a color scale
  • size maps variable to size of object
  • shape maps variable to different shapes

Depending on the geom different mappings are possible, xmin, xend, linetype, alpha, stroke, weight …

Facets

Variables are used to subset (or condition)

Layers

Different data can be mapped onto the same plot, eg observations, and means

Example

ggplot(mpg, 
       aes(
         x=displ, 
         y=hwy, 
         color=class)) + 
  geom_point()

displ is mapped to x
hwy is mapped to y
class is mapped to color.

Common plot descriptions as scripts

Example 1A

How are variables mapped to create this plot?



Code for AUS TB plot 
ggplot(tb_aus, 
       aes(x=year, 
           y=c_newinc)) + 
  geom_point() +
  scale_x_continuous("Year", 
    breaks = seq(1980, 2020, 10), 
    labels = c("80", "90", "00", "10", "20")) +
  ylab("TB incidence")

Example 1B

How are variables mapped to create this plot?



Code for AUS TB plot 
ggplot(tb_aus, aes(x=year, y=c_newinc)) + 
  geom_point() +
  geom_smooth(se=F, colour="#F5191C") +
  scale_x_continuous("Year", breaks = seq(1980, 2020, 10), labels = c("80", "90", "00", "10", "20")) +
  ylab("TB incidence")

Example 2A

How are variables mapped to create this plot?



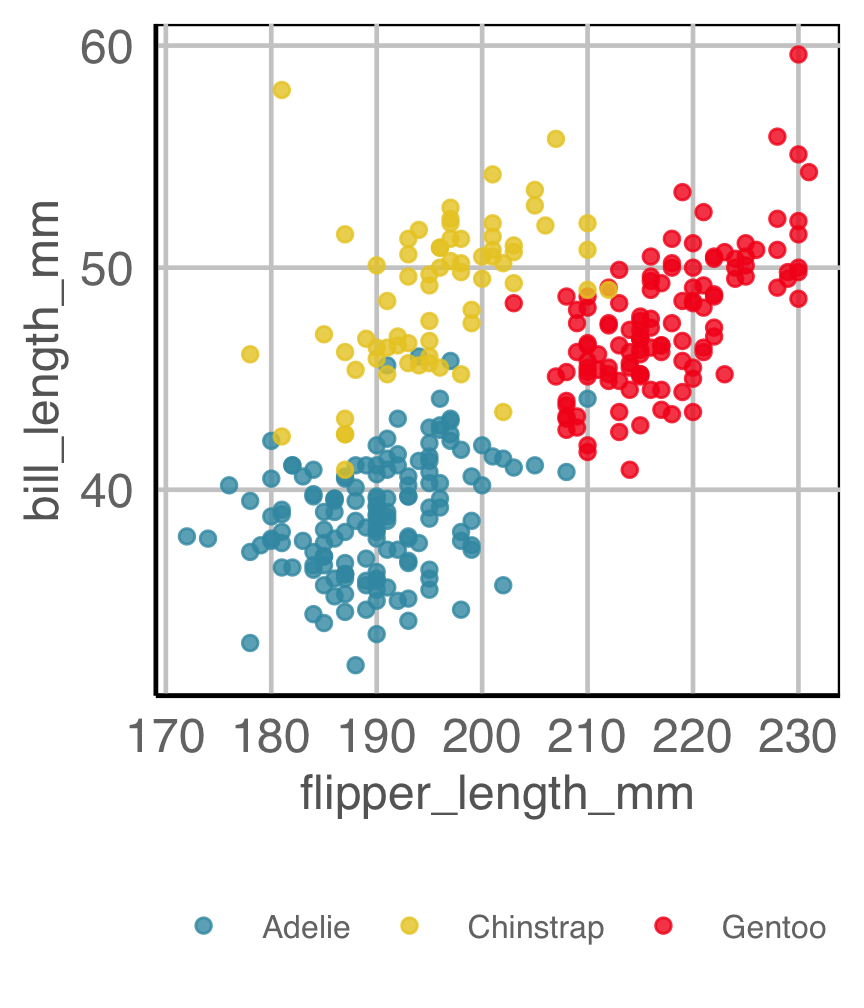
Code for penguins plot 
ggplot(penguins, 
       aes(x=flipper_length_mm, 
           y=bill_length_mm, 
           color=species)) + 
  geom_point(alpha=0.8) +
  scale_color_discrete_divergingx(palette="Zissou 1") +
  theme(legend.title = element_blank(), 
        legend.position = "bottom",
        legend.direction = "horizontal",
        legend.text = element_text(size="8"))

Example 2B

How are variables mapped to create this plot?



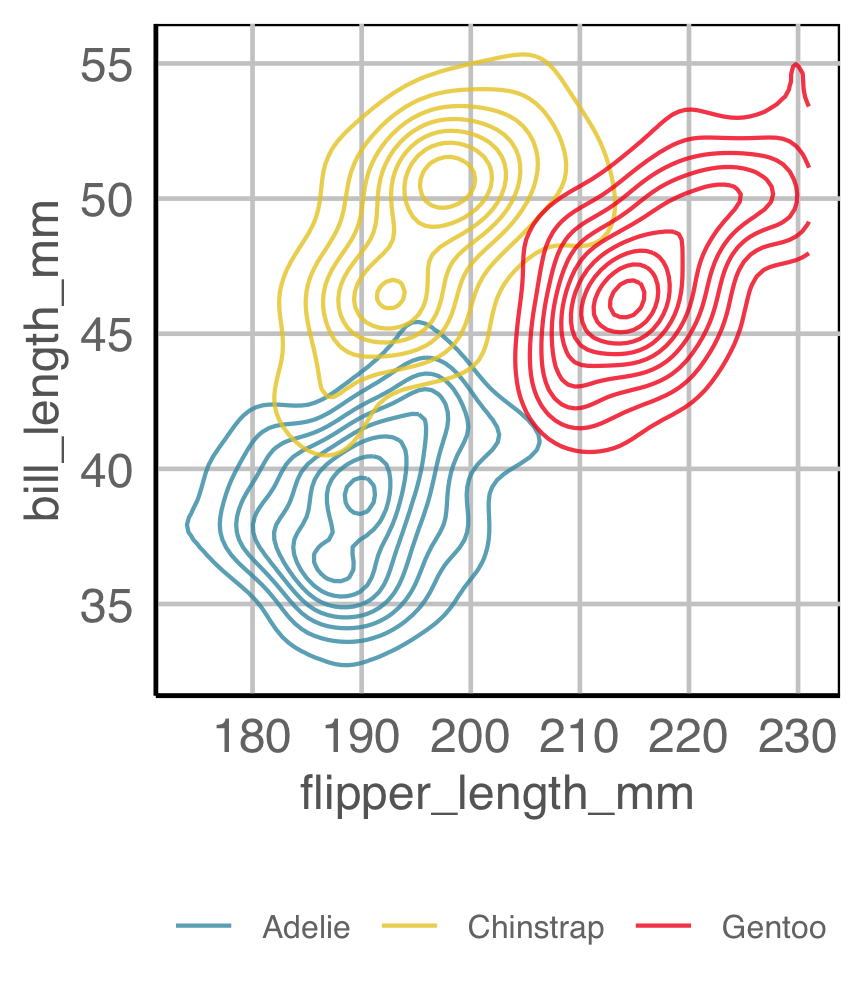
Code for penguins plot 
ggplot(penguins, 
       aes(x=flipper_length_mm, 
           y=bill_length_mm, 
           color=species)) + 
  geom_density2d(alpha=0.8) +
  scale_color_discrete_divergingx(palette="Zissou 1") +
  theme(legend.title = element_blank(), 
        legend.position = "bottom",
        legend.direction = "horizontal",
        legend.text = element_text(size="8"))

Example 3 (1/5)

First get the data in tidy form

tb_aus_sa <- tb_aus |>
  filter(year > 2012) |>
  select(iso3, year, 
         newrel_f014:newrel_f65, 
         newrel_m014:newrel_m65) |>
  pivot_longer(cols=newrel_f014:newrel_m65,
               names_to = "sex_age", 
               values_to = "count") |>
  filter(!is.na(count)) |>
  separate(sex_age, into=c("stuff", 
                           "sex_age")) |>
  mutate(sex = str_sub(sex_age, 1, 1),
         age = str_sub(sex_age, 2, 
                       str_length(sex_age))) |>
  mutate(age = case_when(
    age == "014" ~ "0-14",
    age == "1524" ~ "15-24",
    age == "2534" ~ "25-34",
    age == "3544" ~ "35-44",
    age == "4554" ~ "45-54",
    age == "5564" ~ "55-64",
    age == "65" ~ "65")) |>
  select(iso3, year, sex, age, count)


Example 3 (2/5)

How many ways can we plot all three variables?


geom: bar + position (stack, dodge, fill)

aes:

  • Var 1 to x
  • count to y
  • Var 2 to color
  • Var 3 to facet

geom: point + smooth

aes:

  • Var 1 to x
  • count to y
  • Var 2 to color
  • Var 3 to facet

Example 3 (3/5)

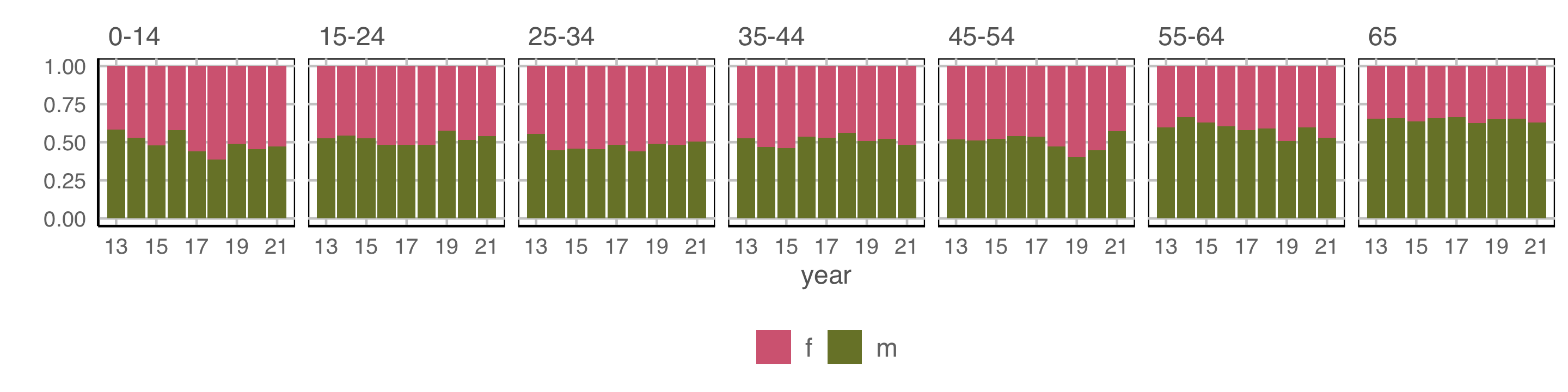
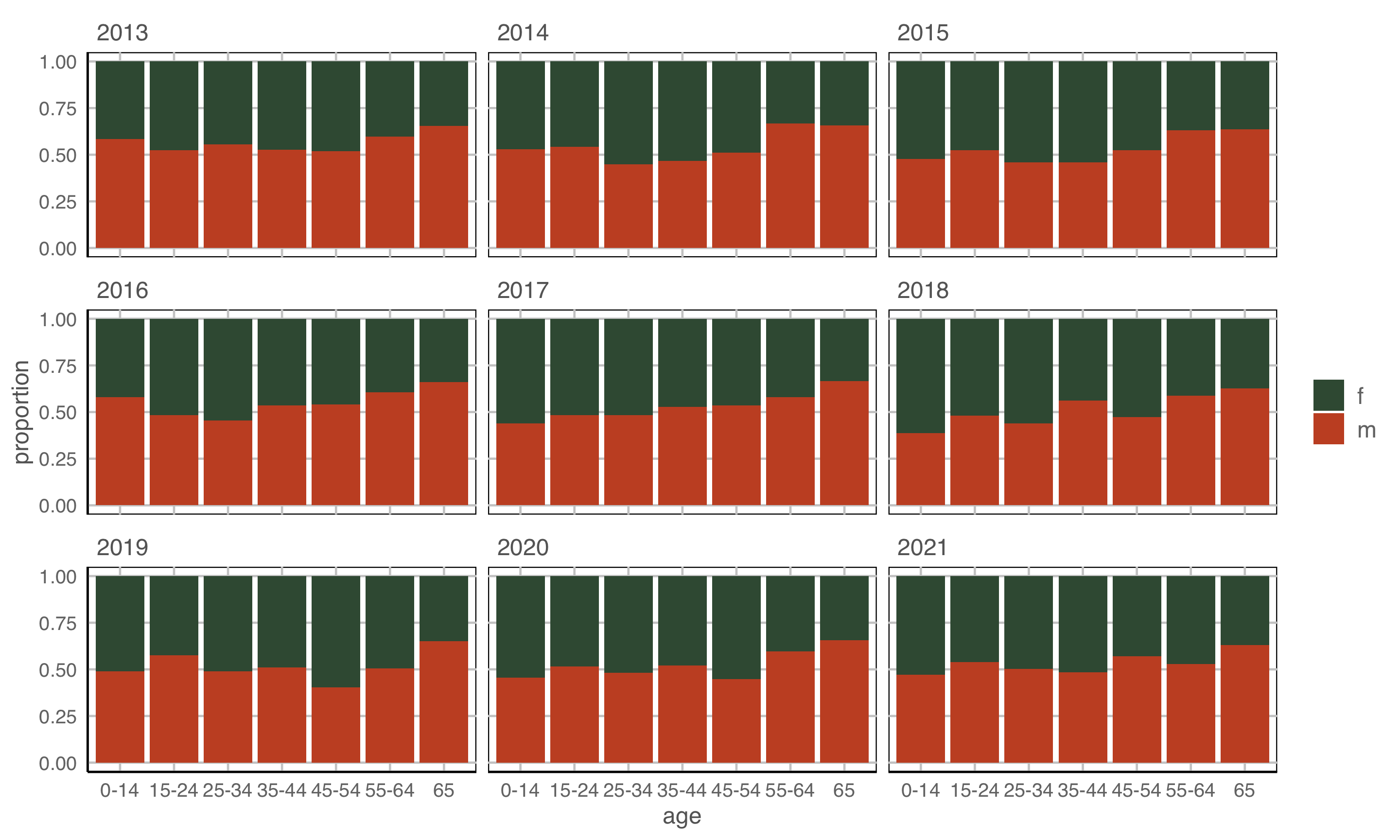
How are variables mapped to create this plot?

geom: bar/position=“fill”

year to x \(~~~~\) count to y \(~~~~\) fill to sex \(~~~~\) facet by age


Observations: Relatively equal proportions, with more incidence among males in older population. No clear temporal trend.

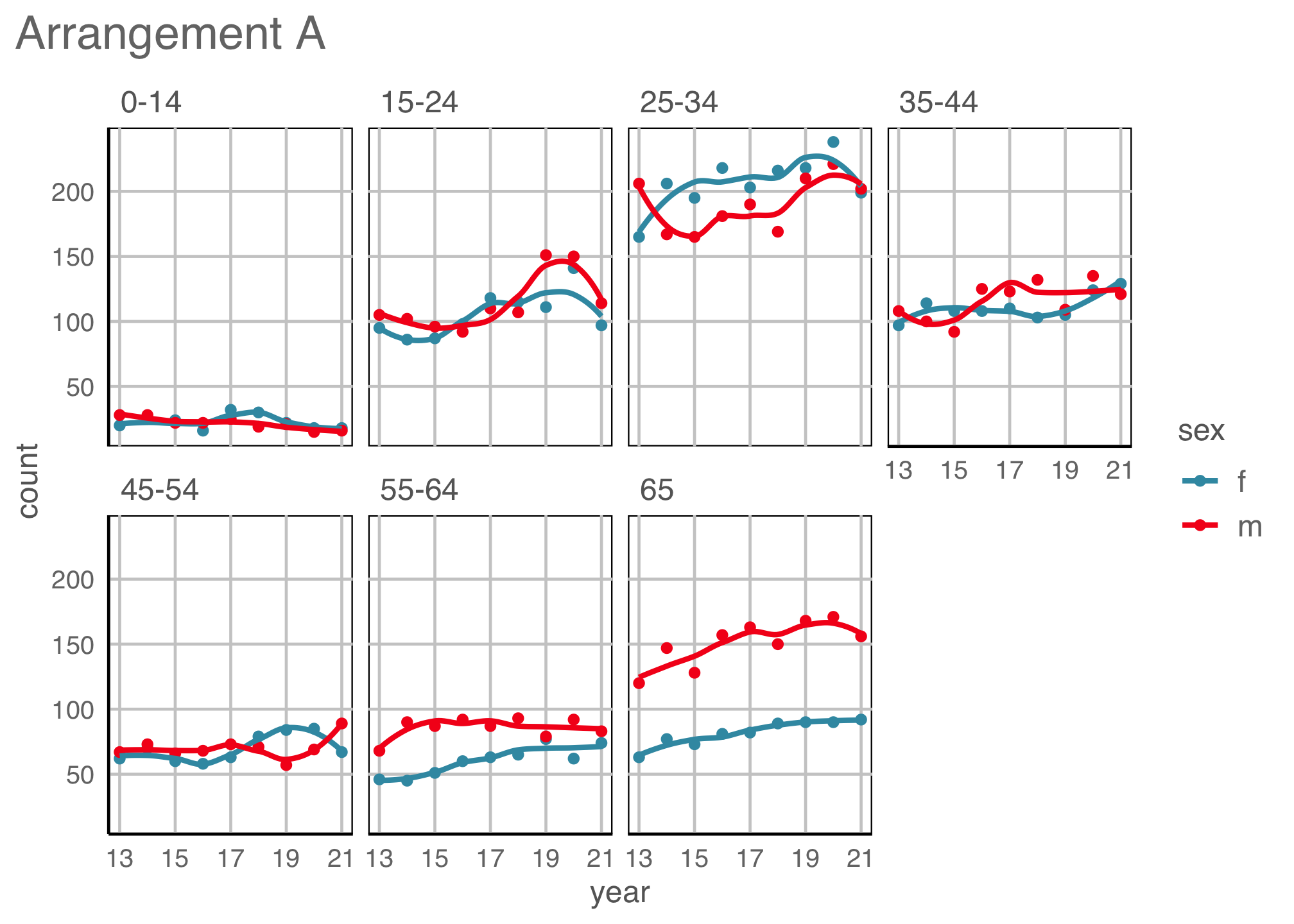
Example 3 (4/5)

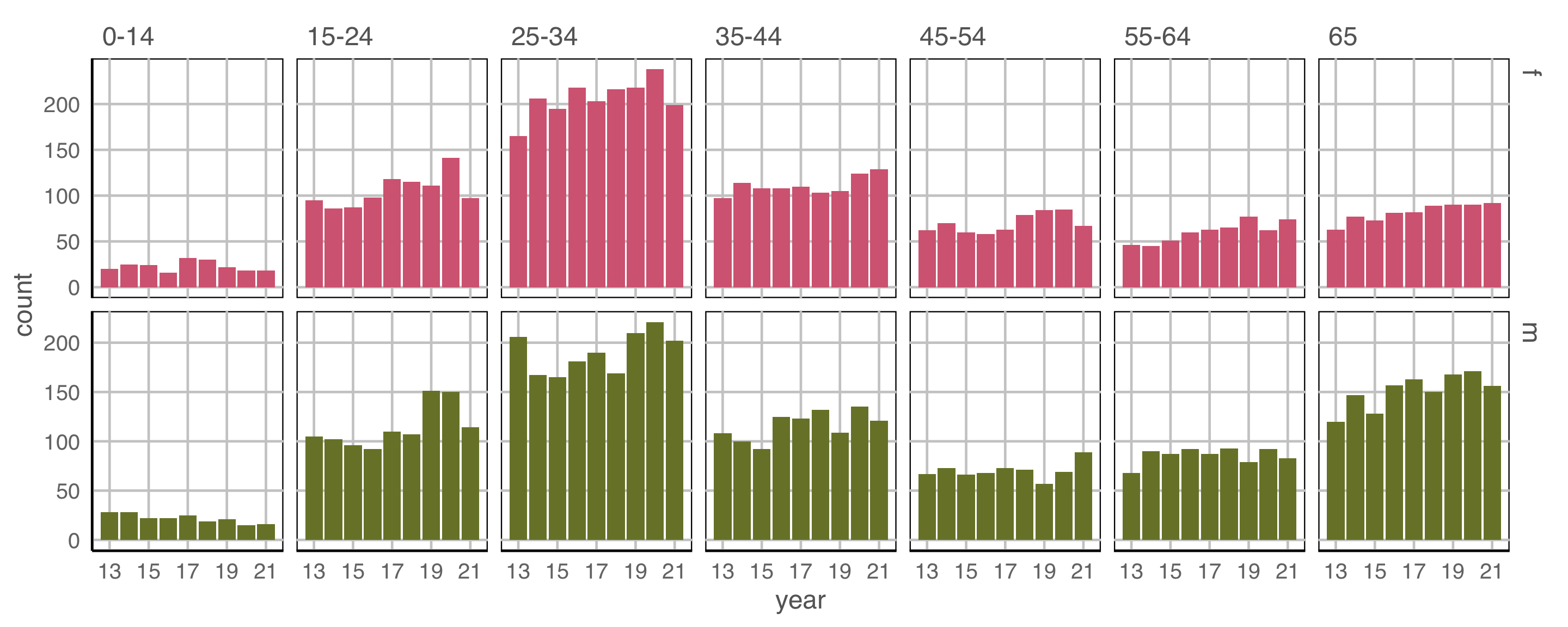
geom: bar

year to x \(~\) count to y \(~\) fill and facet to sex \(~\) facet by age

Incidence is higher among young adult groups, and older males.

Where’s the temporal trend?

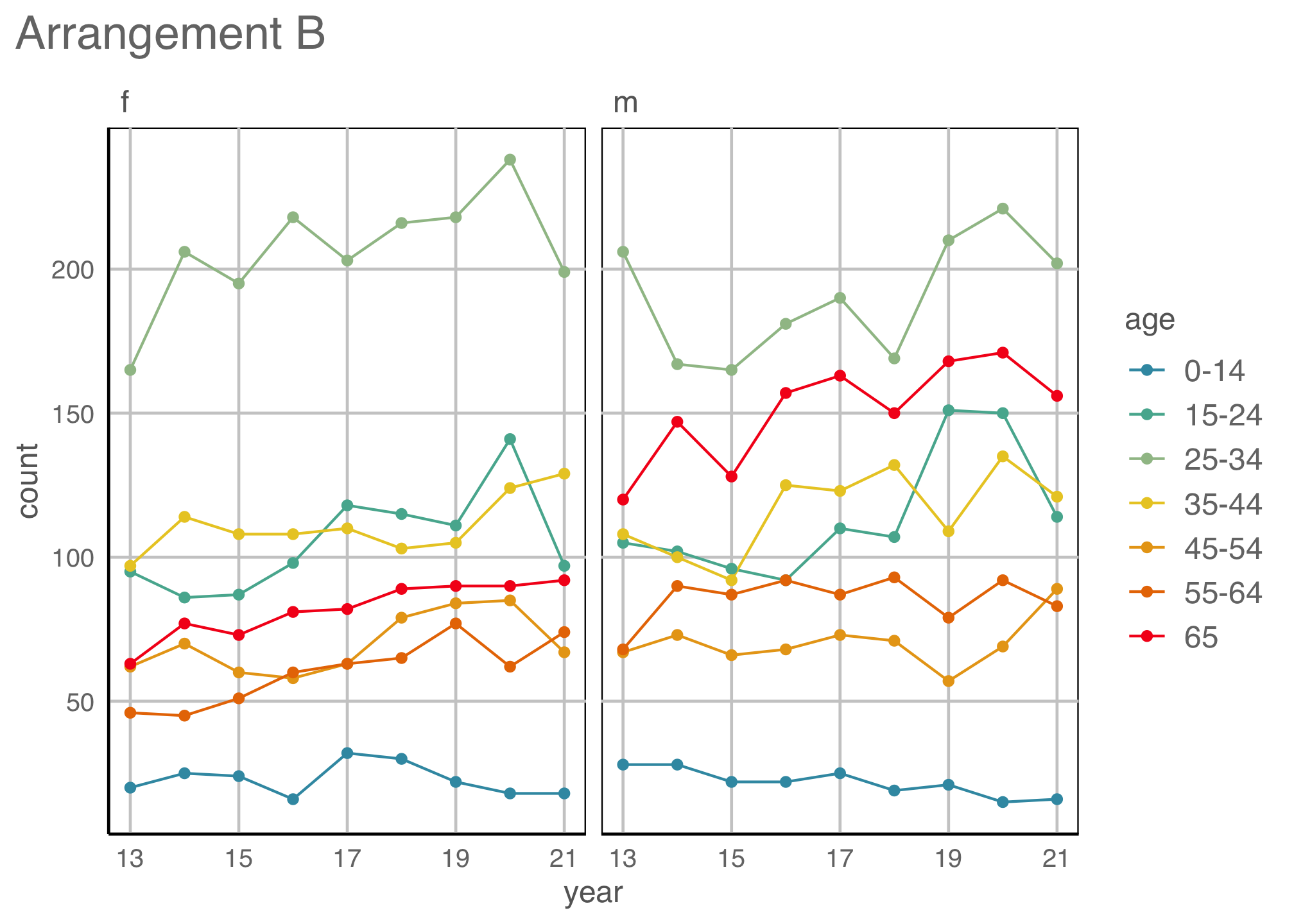
Example 3 (5/5)

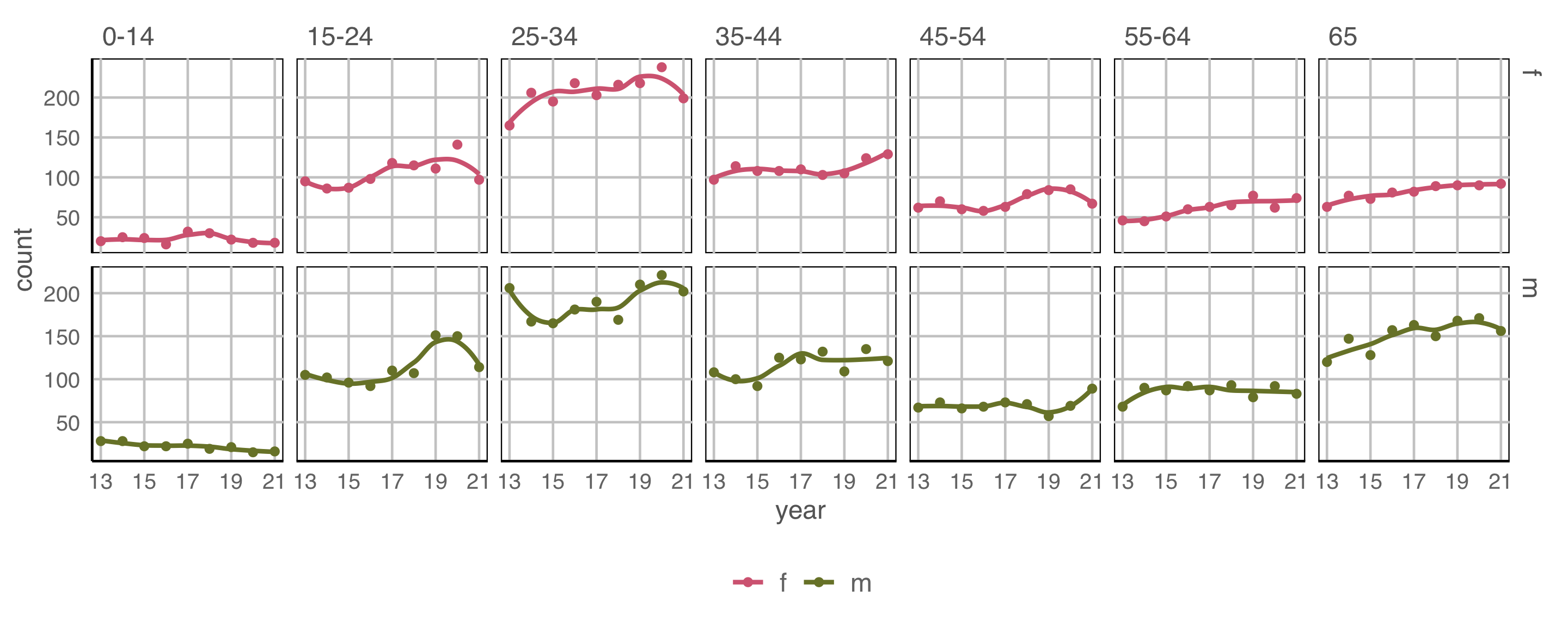
geom: point, smooth

year to x \(~\) count to y \(~\) colour and facet to sex \(~\) facet by age


Temporal trend is only present in some groups.

Tidy data to many plot descriptions

ggplot(tb_aus_sa, 
       aes(x=year, 
           y=count, 
           fill=sex)) + 
  geom_col(position="fill") +
  facet_wrap(~age)
ggplot(tb_aus_sa, 
       aes(x=year, 
           y=count, 
           fill=sex)) + 
  geom_col() +
  facet_grid(sex~age)
ggplot(tb_aus_sa, 
       aes(x=year, 
           y=count, 
           colour=sex)) + 
  geom_point() +
  geom_smooth() +
  facet_grid(sex~age)

?

ggplot(tb_aus_sa, 
       aes(x=age, 
           y=count, 
           fill=sex)) + 
  geom_col(position="fill") +
  facet_wrap(~year)

Re-arrangements

Scaling

This might have slipped under the radar, but different displays had some different scaling of the data:

Slides 6, 27, 28 (Why, Example 3 4,5/5) were constructed with

facet_wrap(..., scales="free_y")


Why?

The emphasis was comparing difference in trend not magnitude of values.

Exercise

  1. Create two new plot arrangements of the Australian TB data. What do they put the focus on?
  2. Change the scaling on one of the plots, where it will change the appearance. How does the information change?

Do’s and don’ts

Plot descriptions

Use a new variable in a single data set - avoid multiple data sets (Tidy data principle)

GOOD

ggplot(tb_sub, aes(x=year, 
                   y=c_newinc, 
                   colour=iso3)) + 
  geom_point() +
  geom_smooth(se=F) +
  facet_wrap(~iso3, ncol=2, 
             scales="free_y") +
  theme(legend.position = "none")

BAD

ggplot() + 
  geom_point(data = tb_aus, 
    aes(x=year, y=c_newinc), 
    colour="#F5191C") +
  geom_point(data = tb_idn, 
    aes(x=year, y=c_newinc), 
    colour="#3B99B1") +
  geom_smooth(data = tb_aus, 
    aes(x=year, y=c_newinc), 
    colour="#F5191C", se=F) +
  geom_smooth(data = tb_idn, 
    aes(x=year, y=c_newinc), 
    colour="#3B99B1", se=F)

Cognitive principles

Hierarchy of mappings

Cleveland and McGill (1984)



Illustrations made by Emi Tanaka

Hierarchy of mappings

  1. Position - common scale (BEST)
  2. Position - nonaligned scale
  3. Length, direction, angle
  4. Area
  5. Volume, curvature
  6. Shading, color (WORST)
  1. scatterplot, barchart
  2. side-by-side boxplot, stacked barchart
  3. piechart, rose plot, gauge plot, donut, wind direction map, starplot
  4. treemap, bubble chart, mosaicplot
  5. chernoff face
  6. choropleth map

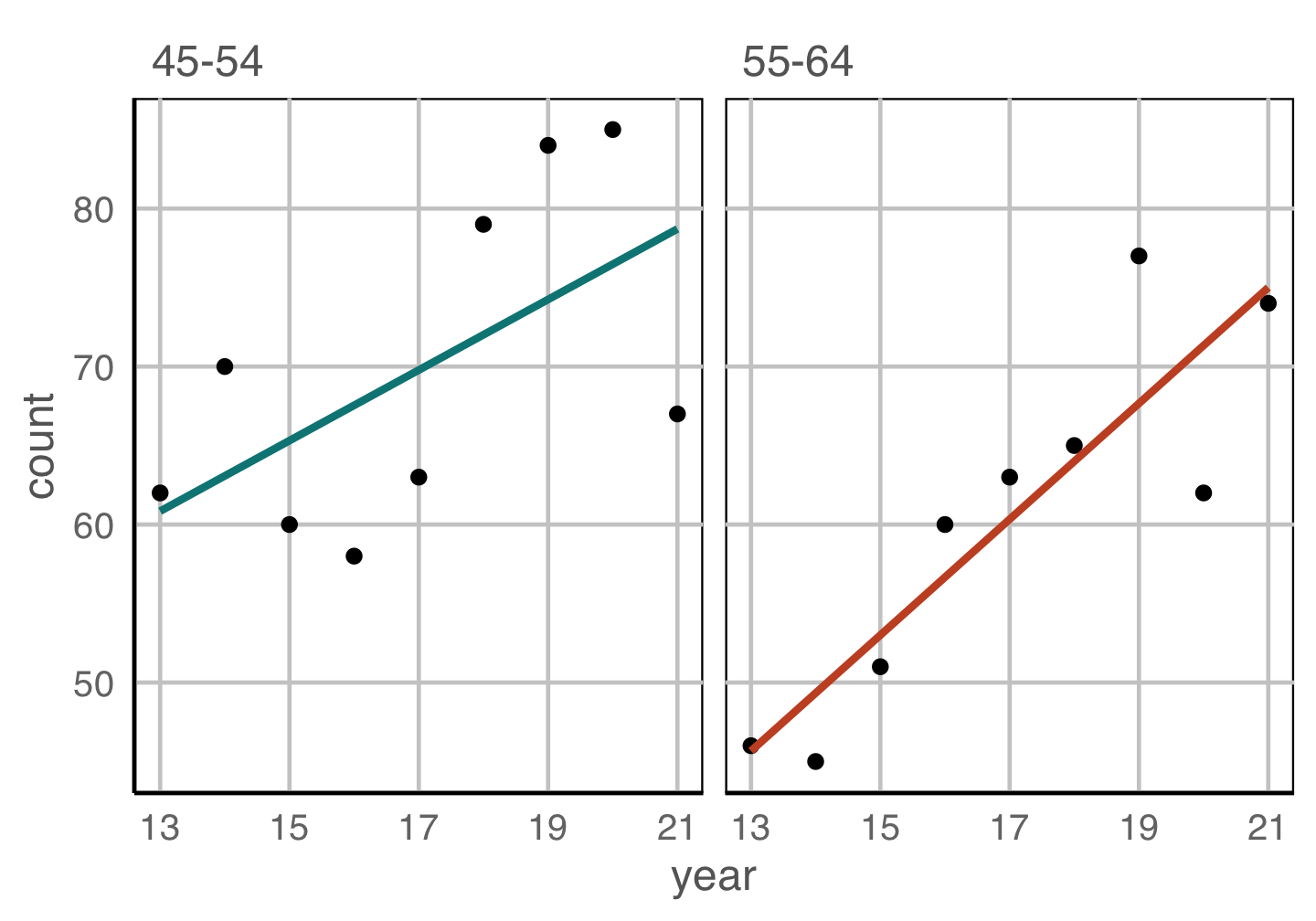
Proximity

Place elements that you want to compare close to each other. If there are multiple comparisons to make, you need to decide which one is most important.

Change blindness

Making comparisons across plots requires the eye to jump from one focal point to another. It may result in not noticing differences.


Exercise

Take the following plot, and make it more difficult to read.

Think about what is it you learn from the plot, and how

  • changing the mapping,
  • using colour, or
  • the geom type

might change what you learn.

library(nullabor)
data(electoral)
ggplot(electoral$polls, 
       aes(x=Democrat, 
           y=Margin)) +
  geom_boxplot()

Take-aways

  • Organise your data so that variables are clear
  • Clearly map your variables to elements of the plot
  • It’s ok to make many plots of the same variables
  • Use proximity effectively

Long exercise

This data is downloaded from ABS Census Datapacks. For this data the goal is to fix the code below for plotting the distribution of household income across Victorian LGAs.

  1. What are the disadvantages of using the code as is?
  2. Rearrange the data into tidy form.
  3. Plot facetted histograms of the distribution of counts by household type.
  4. Plot the data another way, eg density, boxplot.
  5. What do you learn about difference in distributions between family and non-family households?
file = "data/2021Census_G33_VIC_LGA.csv"
hh_income <- read_csv(file)
ggplot(hh_income) +
  geom_histogram(
    aes(Tot_Family_households))
ggplot(hh_income) +
  geom_histogram(
    aes(Tot_Non_family_households))

Solution to long exercise and more

Code for answer 
file = "data/2021Census_G33_VIC_LGA.csv"
hh_income <- read_csv(file)
hh_tidy <- hh_income |>
  select(LGA_CODE_2021, 
         Tot_Family_households,
         Tot_Non_family_households) |> 
  pivot_longer(cols=contains("Tot"), 
                             names_to="hh_type",
                             values_to="count") |>
  mutate(hh_type = str_remove(hh_type, "Tot_")) |>
  mutate(hh_type = str_remove(hh_type, "_households")) |>
  mutate(hh_type = str_remove(hh_type, "_family"))
ggplot(hh_tidy, aes(x=count)) +
  geom_histogram() +
  facet_wrap(~hh_type, ncol=1)
ggplot(hh_tidy, aes(x=count, 
                     colour=hh_type, 
                     fill=hh_type)) +
  geom_density(alpha=0.5) +
  scale_color_discrete_divergingx() +
  scale_fill_discrete_divergingx() 
ggplot(hh_tidy, aes(x=hh_type,
                     y=count)) +
  geom_boxplot() 
ggplot(hh_tidy, aes(x=hh_type,
                     y=count)) +
  geom_quasirandom()
Code for proportions 
hhi_tidy <- hh_income |>
  select(LGA_CODE_2021, 
         contains("_Tot"), -Tot_Tot) |>
  pivot_longer(cols=contains("Tot"), 
      names_to="income_cat",
      values_to="count") |>
  mutate(income_cat = str_remove(income_cat, "_Tot")) |>
  mutate(income_cat = str_remove(income_cat, "HI_")) |>
  mutate(income_cat = str_remove(income_cat, "_Nil_income")) |>
  mutate(income_cat = str_remove(income_cat, "_income_stated")) |>
  mutate(income_cat = str_remove(income_cat, "_incomes_not_stated")) |>
  group_by(income_cat) |>
  mutate(prop = count/sum(count)) |>
  dplyr::filter(!(income_cat %in% 
     c("Partial", "All", "Negative"))) |>
  separate(income_cat, into=c("cmin", "cmax")) |>
  mutate(cmax = str_replace(cmax, "more", "5000")) |>
  mutate(income = (as.numeric(cmin) +
           as.numeric(cmax))/2) |>
  select(-cmin, cmax)

hhi_tidy |>
  dplyr::filter(LGA_CODE_2021 %in%
     sample(unique(hhi_tidy$LGA_CODE_2021), 8)) |>
  ggplot(aes(x=income, y=count)) +
    facet_wrap(~LGA_CODE_2021, ncol=4) +
    geom_line()

End of session 1

Creative Commons License
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

https://dicook.github.io/tutorial_effective_data_plots/