Visualising High-dimensional Data with R

Session 2

Dianne Cook, Monash University
Ursula Laa, BOKU

Session 2

Outline

time topic
3:00-3:15 More on dimension reduction
3:15-4:00 Understanding clusters in data using visualisation
4:00-4:40 Building better classification models with visual input
4:40-5:00 Bring your own data!

Dimension reduction

Non-linear dimension reduction (1/2)

Find some low-dimensional layout of points which approximates the distance between points in high-dimensions, with the purpose being to have a useful representation that reveals high-dimensional patterns, like clusters.

Multidimensional scaling (MDS) is the original approach:

\[ \mbox{Stress}_D(x_1, ..., x_n) = \left(\sum_{i, j=1; i\neq j}^n (d_{ij} - d_k(i,j))^2\right)^{1/2} \] where \(D\) is an \(n\times n\) matrix of distances \((d_{ij})\) between all pairs of points, and \(d_k(i,j)\) is the distance between the points in the low-dimensional space.

PCA is a special case of MDS. The result from PCA is a linear projection, but generally MDS can provide some non-linear transformation.

Many variations being developed:

  • t-stochastic neighbourhood embedding (t-SNE): compares interpoint distances with a standard probability distribution (eg \(t\)-distribution) to exaggerate local neighbourhood differences.
  • uniform manifold approximation and projection (UMAP): compares the interpoint distances with what might be expected if the data was uniformly distributed in the high-dimensions.

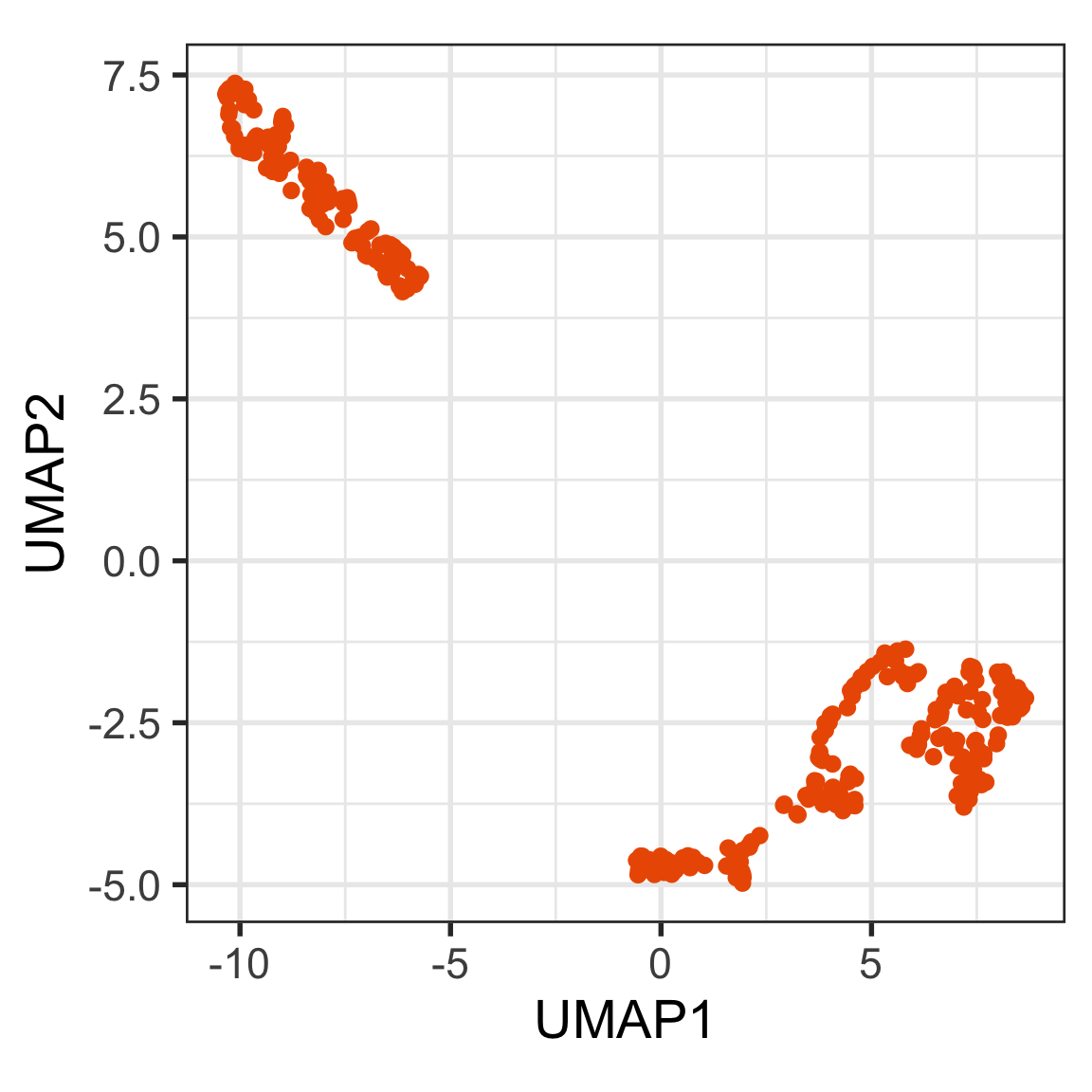
NLDR can be useful but it can also make some misleading representations.

Non-linear dimension reduction (2/2)

UMAP 2D representation

Tour animation of the same data

Grand tour showing the 4D penguins data. Two clusters are easily seen, and a third is plausible.

Your turn

Which is the best representation, t-SNE or UMAP, of this 9D data?

You can use this code to read the data and view in a tour:

pbmc <- readRDS("data/pbmc_pca_50.rds")
animate_xy(pbmc[,1:9])

05:00

Clustering

Method 1: Spin-and-brush

library(detourr)
set.seed(645)
detour(p_tidy_std[,2:5], 
       tour_aes(projection = bl:bm)) |>
       tour_path(grand_tour(2), fps = 60, 
                 max_bases=40) |>
       show_scatter(alpha = 0.7, 
                    axes = FALSE)

DEMO

What are clusters?

Ideal thinking of neatly separated clusters, but it is rarely encountered in data




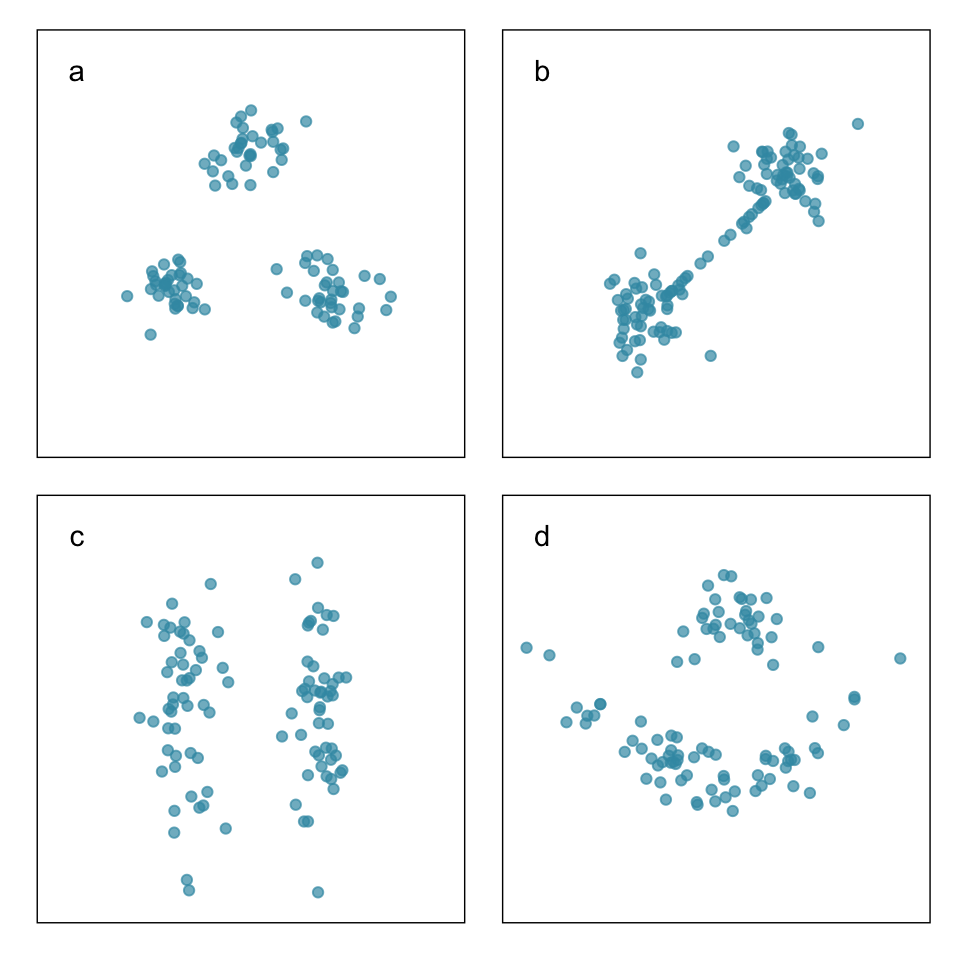
Objective is to organize the cases into groups that are similar in some way. You need a measure of similarity (or distance).

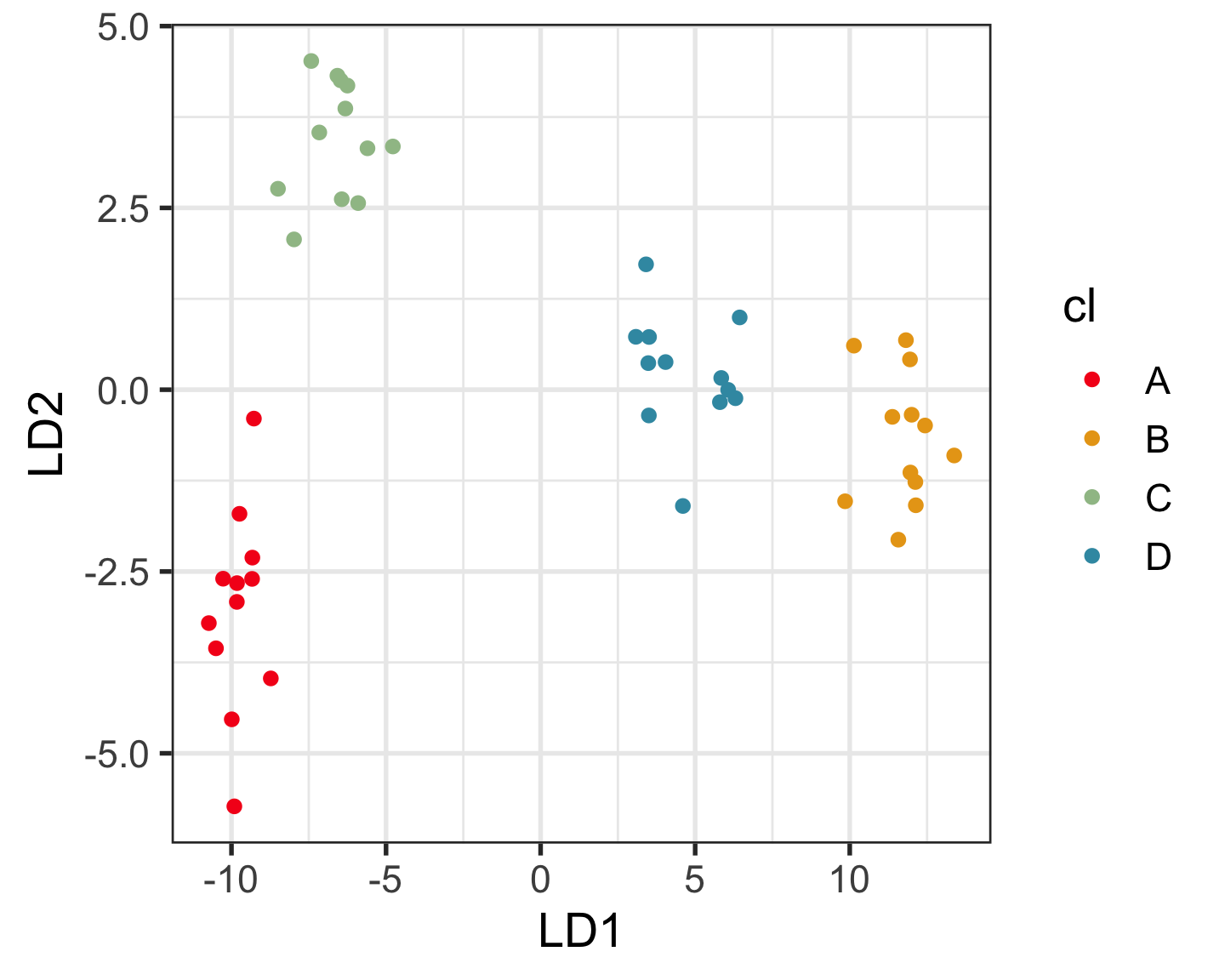
Why visualise? Which is the better?

Nuisance cases

Nuisance variables

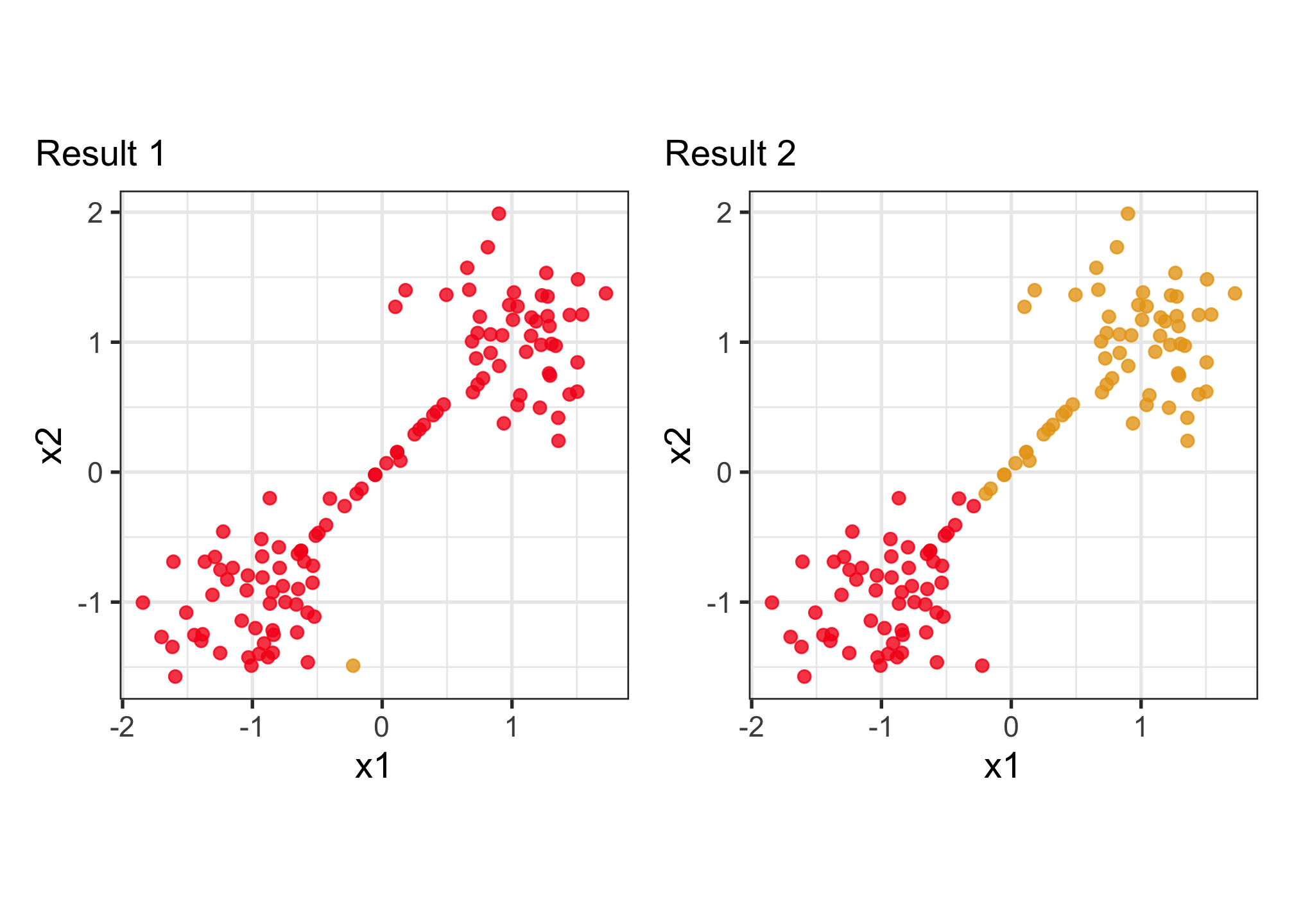
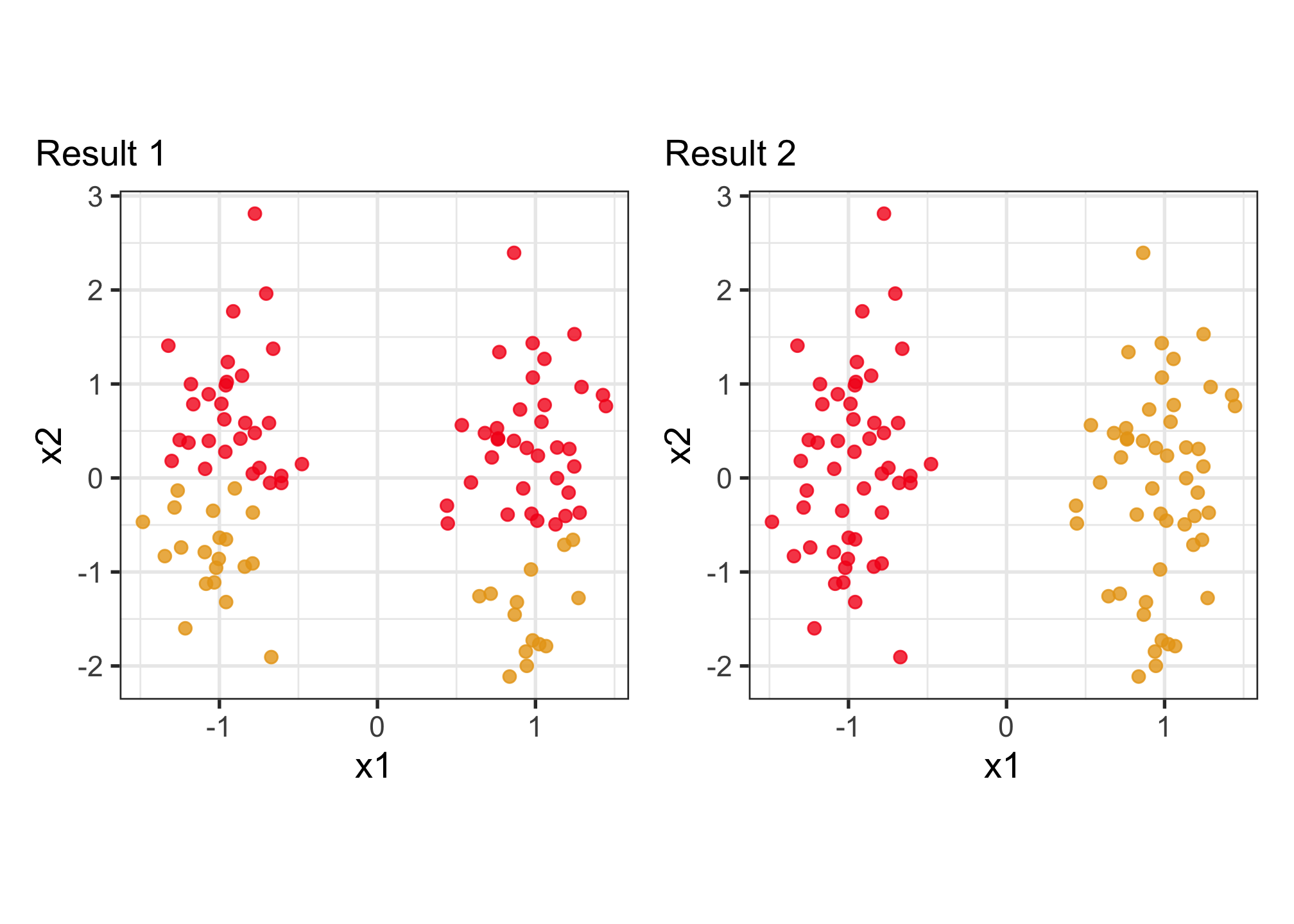
To decide on a best result, you need to see how it divides the data into clusters. The cluster statistics, like dendrogram, or cluster summaries, or gap statistics might all look good but the result is bad. You need to see the model in the data space!

Model-based clustering (1/3)

Model-based clustering fits a multivariate normal mixture model to the data.

\[ \Sigma_k = \lambda_kD_kA_kD_k^\top, ~~~k=1, \dots, g \]

where

\(\Sigma_k\) is the variance-covariance of cluster \(k\),

\(g=\)number of clusters,

\(D_k\) describes the orientation of a cluster,

\(A_k\) describes the variance in different variables,

\(\lambda_k\) is an overall size.

Model-based clustering (2/3)

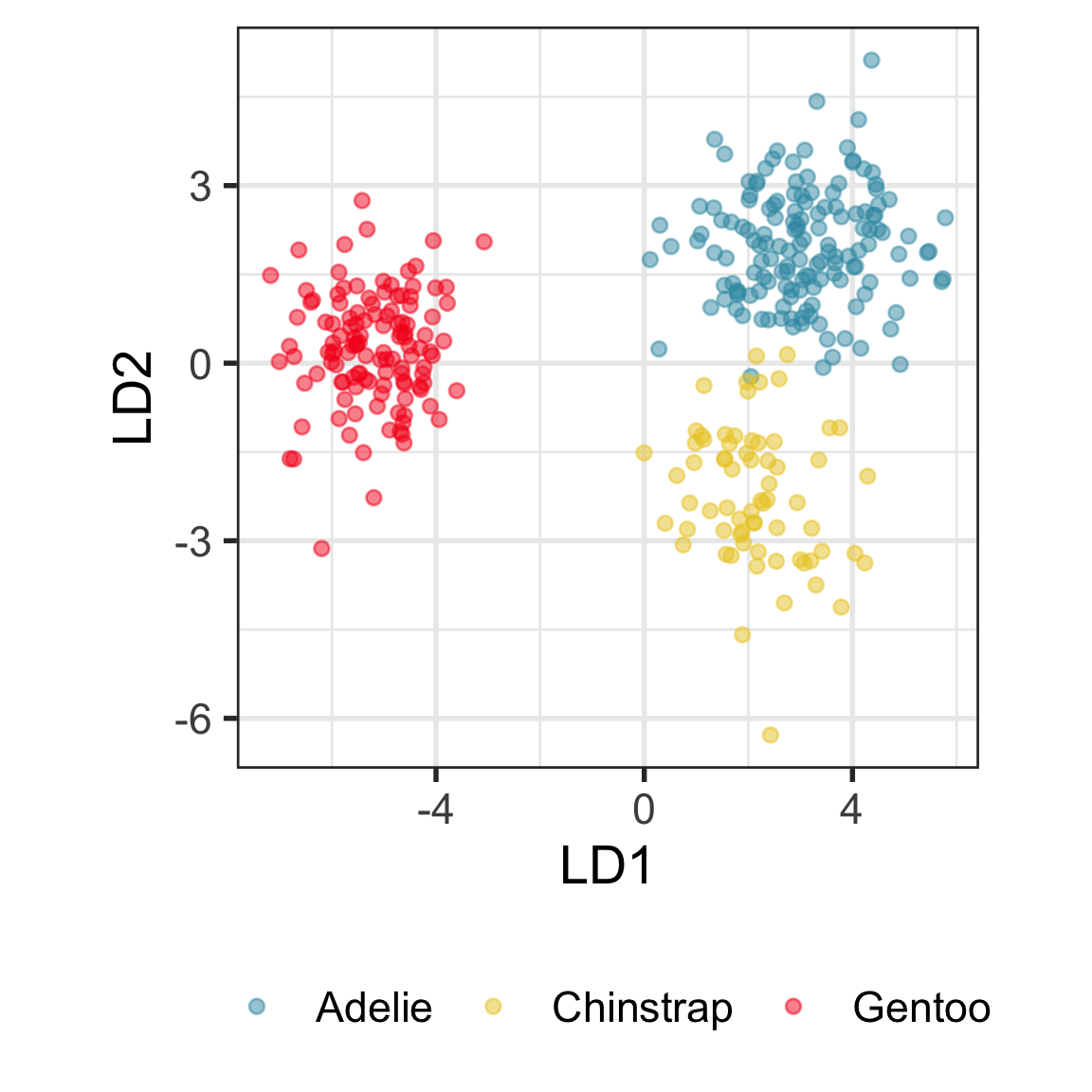
Clustering this data. What do you expect?

Can we assume the shape of the clusters is elliptical?

Volume, Shape, Orientation

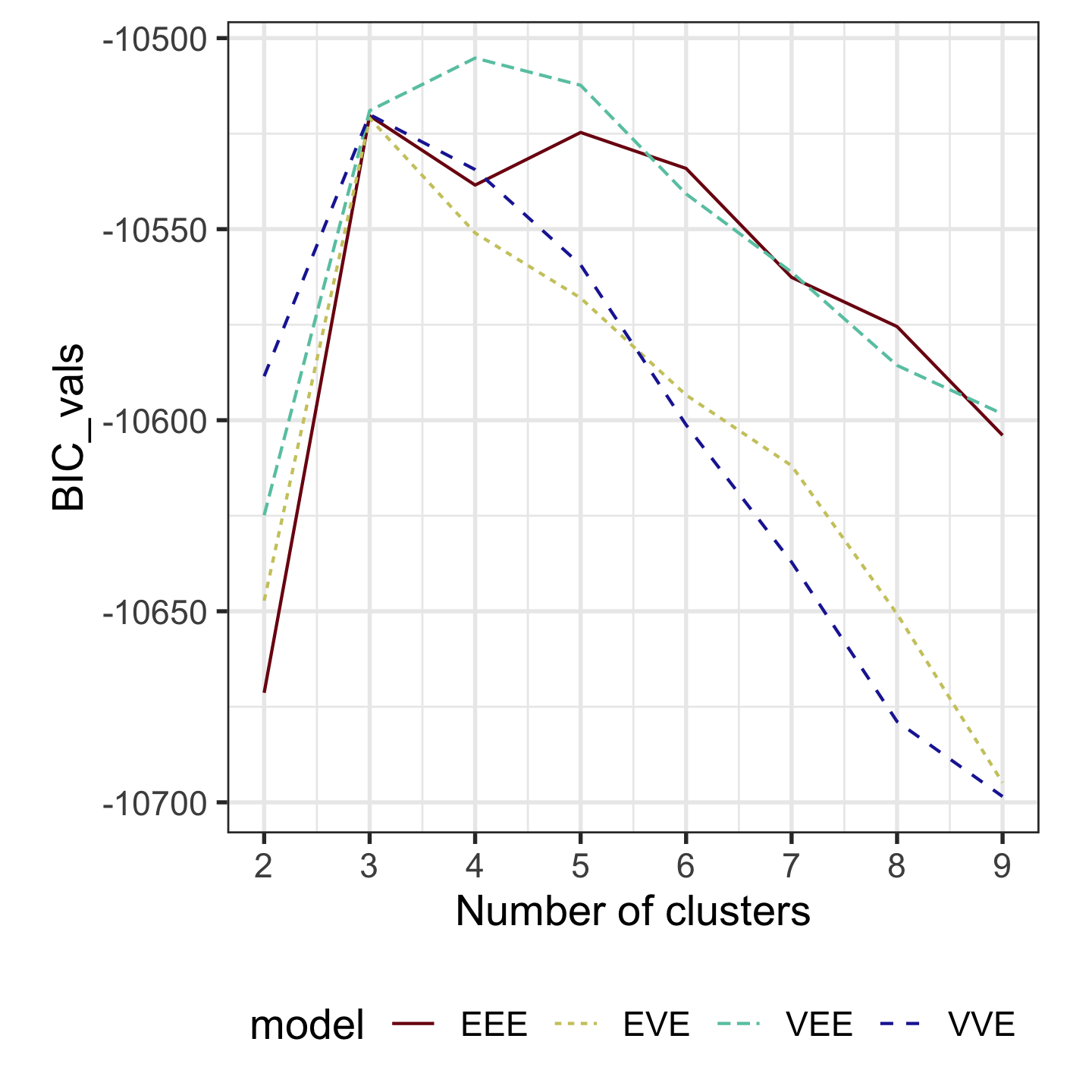
Model-based clustering (3/3)

Four-cluster VEE

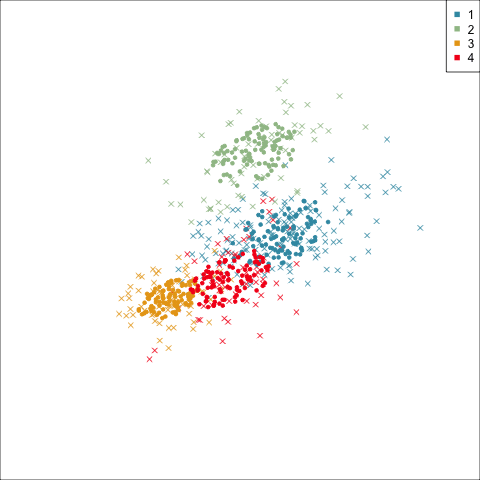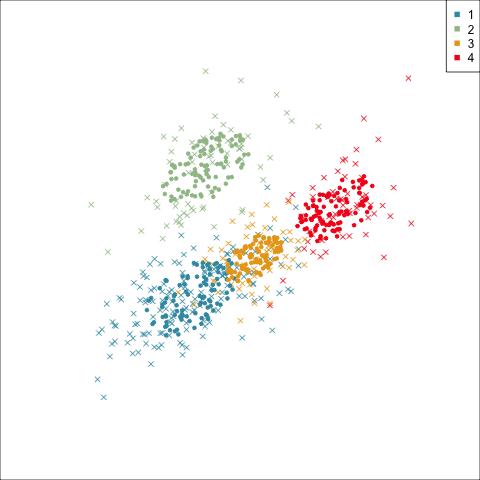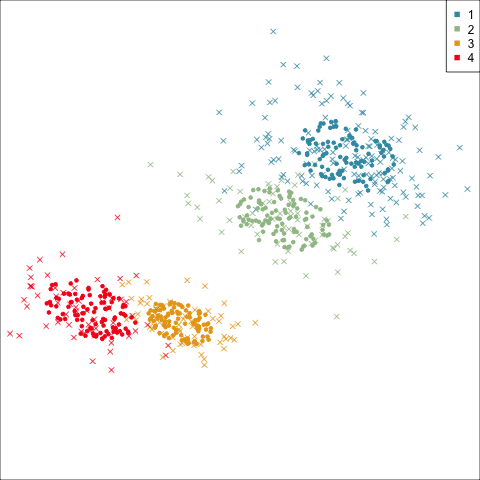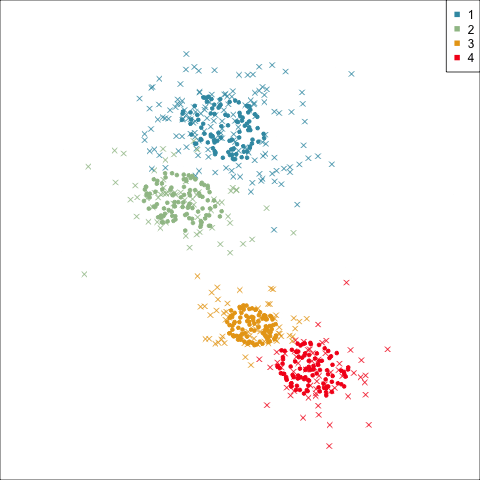
Three-cluster EEE

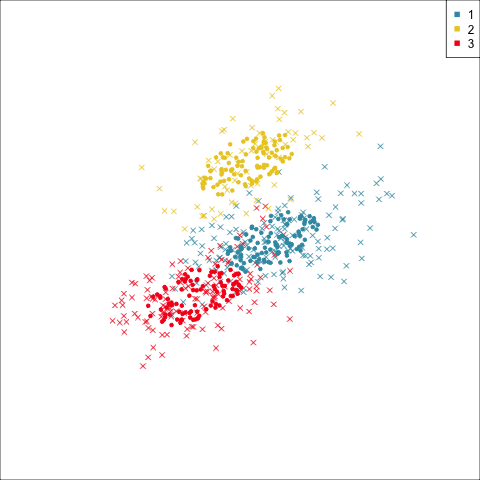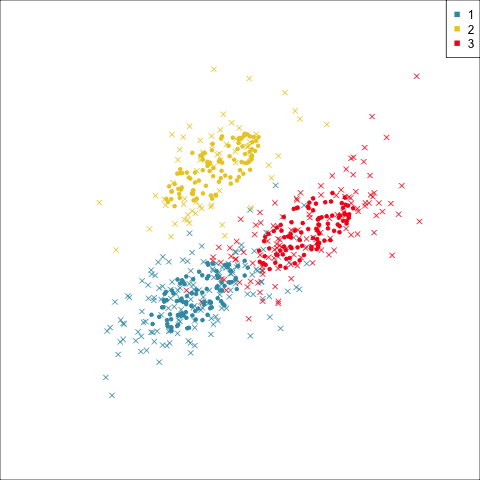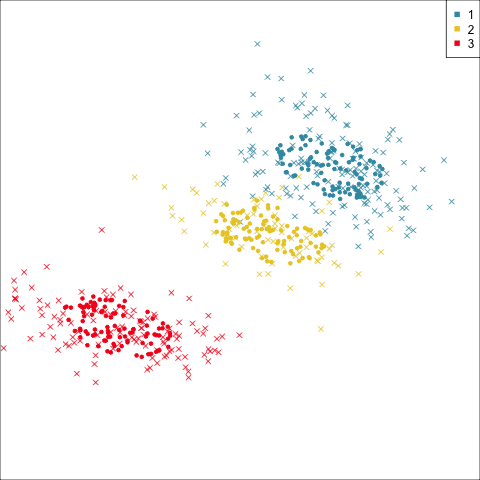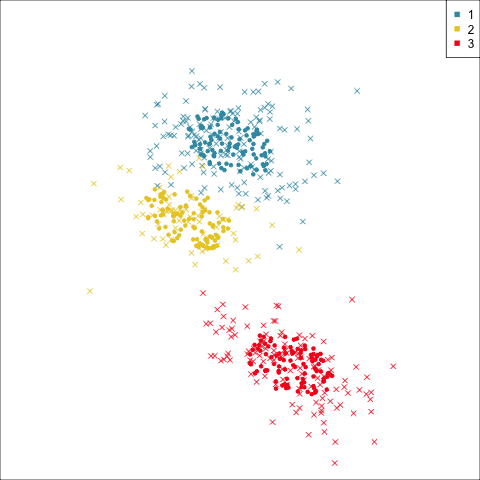
Models (ellipses) are overlaid on the data. Which is the best fit?

How do you draw ellipses in high-d?

Extract the estimated model parameters

p_mc <- Mclust(
  p_tidy[,2:5], 
  G=3, 
  modelNames = "EEE")
p_mc$parameters$mean
   [,1] [,2] [,3]
bl   39   48   49
bd   18   15   18
fl  190  217  196
bm 3693 5076 3754
p_mc$parameters$variance$sigma[,,1]
      bl    bd     fl     bm
bl   8.4   1.6    8.3    755
bd   1.6   1.2    3.5    318
fl   8.3   3.5   42.5   1751
bm 754.7 318.4 1751.2 211467

Generate data that represents the ellipse(s) to overlay on the data.

p_mce <- mc_ellipse(p_mc)
  • Sample points uniformly on a pD sphere
  • Transform into an ellipse using the inverse variance-covariance matrix

Your turn

Use the spin-and-brush approach to extract the clusters from the c1 data.

05:00

Classification

What should you visualise?

  • Understand any clustering related to the known classes.
  • Obtain a sense of where boundaries might be placed.
  • Examine where the fitted model fits the data well, and where poorly.
  • Understand the misclassifications, whether they are reasonable given uncertainty in the data, or due to an ill-fitting or poorly specified model.
  • Understand what can happen with model fitting and pattern recognition with sparse data.

Example: Linear DA

Linear discriminant analysis is the ideal classifier for this data.

Random forests (1/2)

A random forest is the simplest classifier to fit for complicated boundaries. It is built from multiple trees generated by randomly sampling the cases and the variables. The random sampling (with replacement) of cases has the fortunate effect of creating a training (“in-bag”) and a test (“out-of-bag”) sample for each tree computed. The most beautiful results are obtaining diagnostics that help us to assess the model are the votes, the measure of variable importance, and the proximity matrix.


Call:
 randomForest(formula = cause ~ ., data = bushfires_sub, importance = TRUE) 
               Type of random forest: classification
                     Number of trees: 500
No. of variables tried at each split: 7

        OOB estimate of  error rate: 11%
Confusion matrix:
            accident arson burning_off lightning
accident          73     3           0        62
arson             11     8           1        17
burning_off        3     0           3         3
lightning         14     0           0       823
            class.error
accident          0.471
arson             0.784
burning_off       0.667
lightning         0.017

Random forests (2/2)

The votes matrix can be considered to be predictive probabilities, where the values for each observation sum to 1. With 3 classes it is a 2D triangle. For 4 or more classes it is a simplex and can be examined in a tour.

Votes matrix for the random forest fit on penguins

Votes matrix for bushfire model fit

Code 
# Create votes matrix data
bushfires_rf_votes <- bushfires_rf$votes %>%
  as_tibble() %>%
  mutate(cause = bushfires_sub$cause)

# Project 4D into 3D
proj <- t(geozoo::f_helmert(4)[-1,])
b_rf_v_p <- as.matrix(bushfires_rf_votes[,1:4]) %*% proj
colnames(b_rf_v_p) <- c("x1", "x2", "x3")
b_rf_v_p <- b_rf_v_p %>%
  as.data.frame() %>%
  mutate(cause = bushfires_sub$cause)
  
# Add simplex
simp <- simplex(p=3)
sp <- data.frame(simp$points)
colnames(sp) <- c("x1", "x2", "x3")
sp$cause = ""
b_rf_v_p_s <- bind_rows(sp, b_rf_v_p) %>%
  mutate(cause = factor(cause))
labels <- c("accident" , "arson", 
                "burning_off", "lightning", 
                rep("", nrow(b_rf_v_p)))

animate_xy(b_rf_v_p_s[,1:3], col = b_rf_v_p_s$cause, 
           axes = "off", half_range = 1.3,
           edges = as.matrix(simp$edges),
           obs_labels = labels)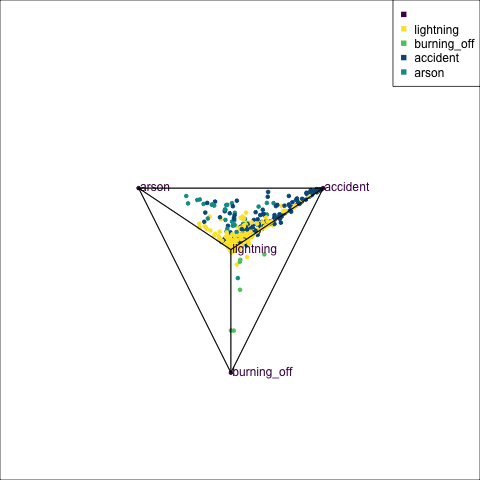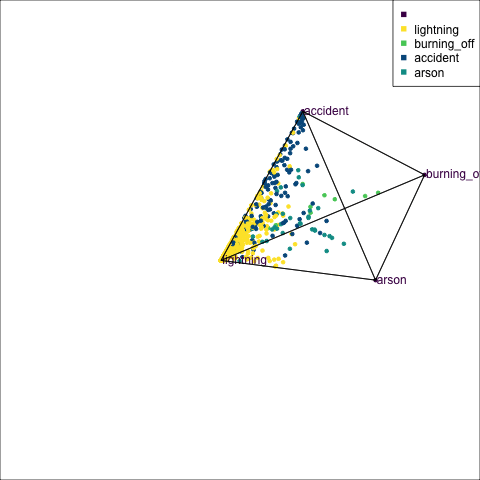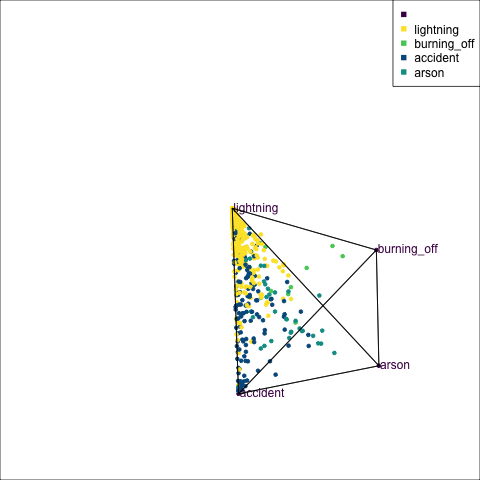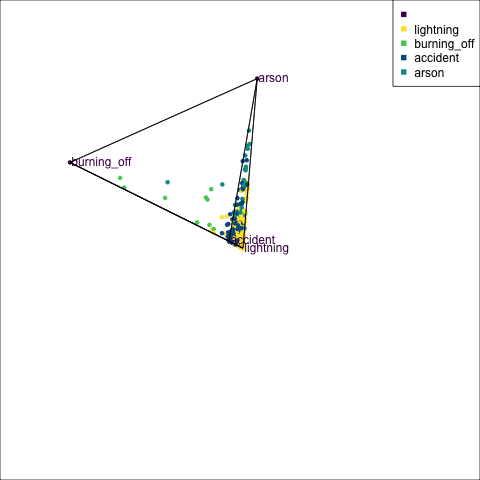

Exploring misclassifications

library(crosstalk)
library(plotly)
library(RColorBrewer)
p_cl <- p_tidy_std |>
  mutate(pspecies = predict(p_lda, p_tidy)$class) |>
  dplyr::select(bl:bm, species, pspecies) |>
  mutate(sp_jit = jitter(as.numeric(species), 0.5),
         psp_jit = jitter(as.numeric(pspecies), 0.5))
p_cl_shared <- SharedData$new(p_cl)

detour_plot <- detour(p_cl_shared, tour_aes(
  projection = bl:bm,
  colour = species)) |>
    tour_path(grand_tour(2), 
                    max_bases=50, fps = 60) |>
       show_scatter(alpha = 0.9, axes = FALSE,
                    width = "100%", height = "450px",
                    palette = brewer.pal(3, "Dark2"))

conf_mat <- plot_ly(p_cl_shared, 
                    x = ~psp_jit,
                    y = ~sp_jit,
                    color = ~species,
                    colors = brewer.pal(3, "Dark2"),
                    height = 450) |>
  highlight(on = "plotly_selected", 
              off = "plotly_doubleclick") %>%
    add_trace(type = "scatter", 
              mode = "markers")
  
bscols(
     detour_plot, conf_mat,
     widths = c(5, 6)
 )

DEMO

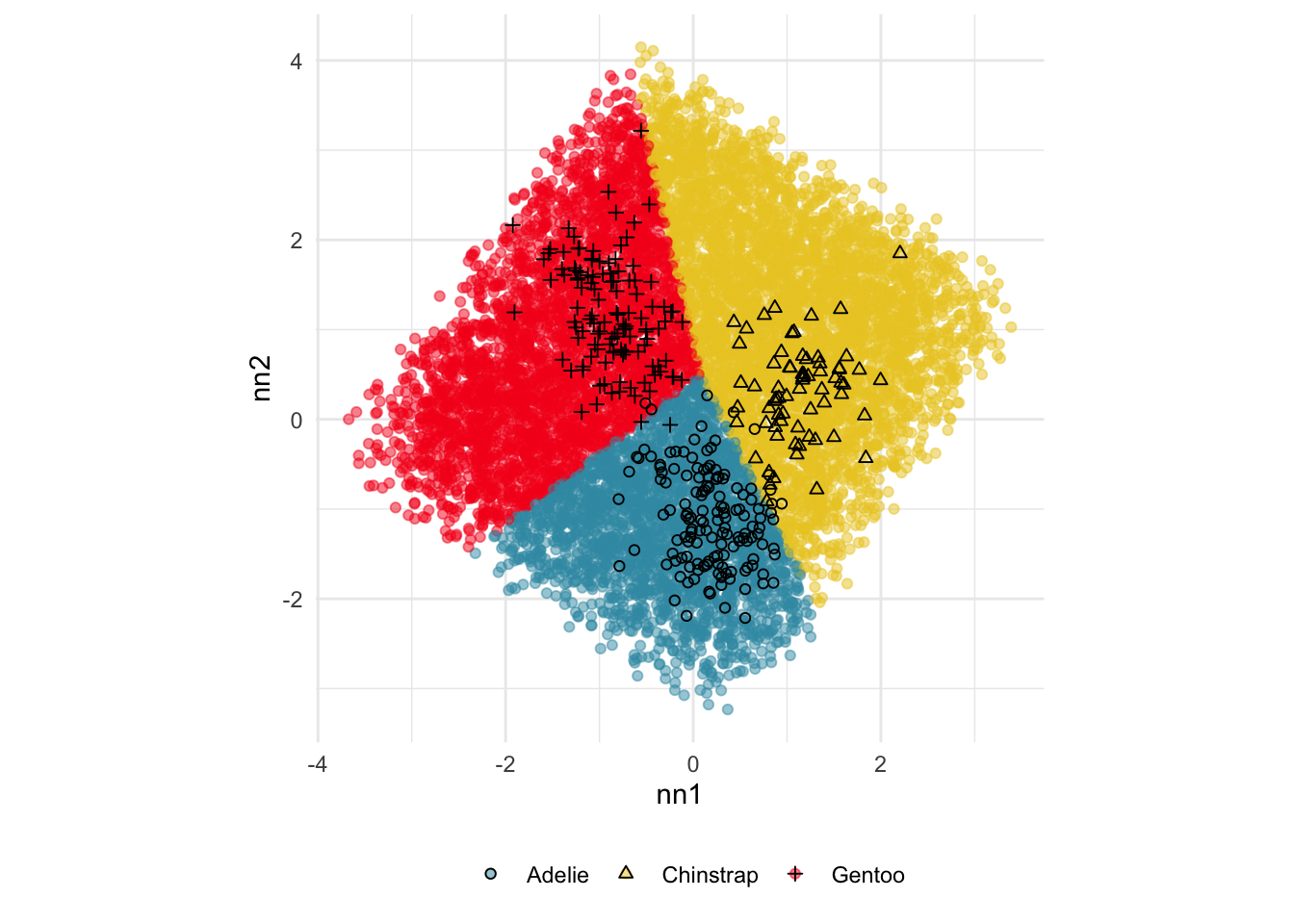
Your turn

Explore the misclassifications in the random forest fit of the penguins data, using the code provided in the slides2.R file.

05:00

Cautions about high-dimensions

Space is big.

What might appear to be structure is only sampling variability.

\(n=48, p=40\)

Permutation is your friend, for high-dimensional data analysis.

Permute the class labels.

set.seed(951)
ws <- w |>
  mutate(cl = sample(cl))

Other compelling pursuits

Explore and compare the boundaries of different models using the slice tour.

Dissect and explore the operation of a neural network.

Bring your own data

Your turn

  • Examine data of your own choice
  • Share what you learn about your data, here

If you don’t have your own data, try looking at the risk_MSA which contains survey responses on six types of risks (recreational, health, career, financial, safety and social) perceived with Australian tourism, collected in 2015, used in Dolnicar et al, 2018.

Where to learn more

All of the material presented today comes from

Cook and Laa (2024) Interactively exploring high-dimensional data and models in R

Software:

\(~~\) \(~~\) \(~~\) \(~~\)

End of session 2

Creative Commons License
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.