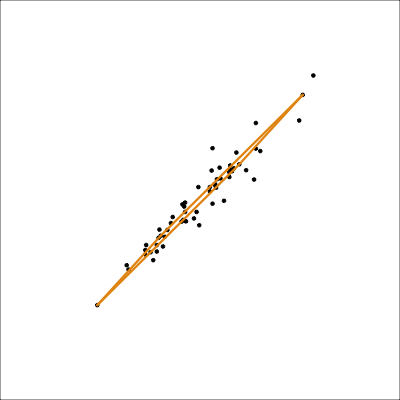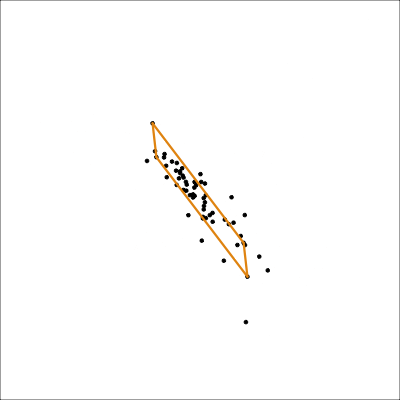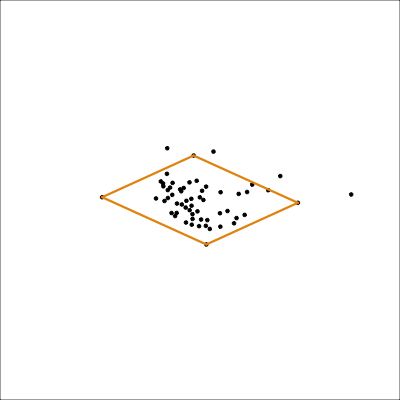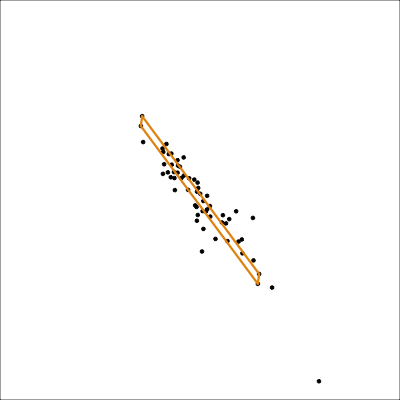Visualising High-dimensional Data with R

Session 1

Dianne Cook, Monash University

Session 1

Outline

time	topic
1:30-1:40	Introduction: What is high-dimensional data, why visualise and overview of methods
1:50-2:10	Basics of linear projections, and recognising high-d structure
2:10-2:30	Effectively reducing your data dimension, in association with non-linear dimension reduction
2:30-3:00	BREAK

Introduction

What is high-dimensional space?

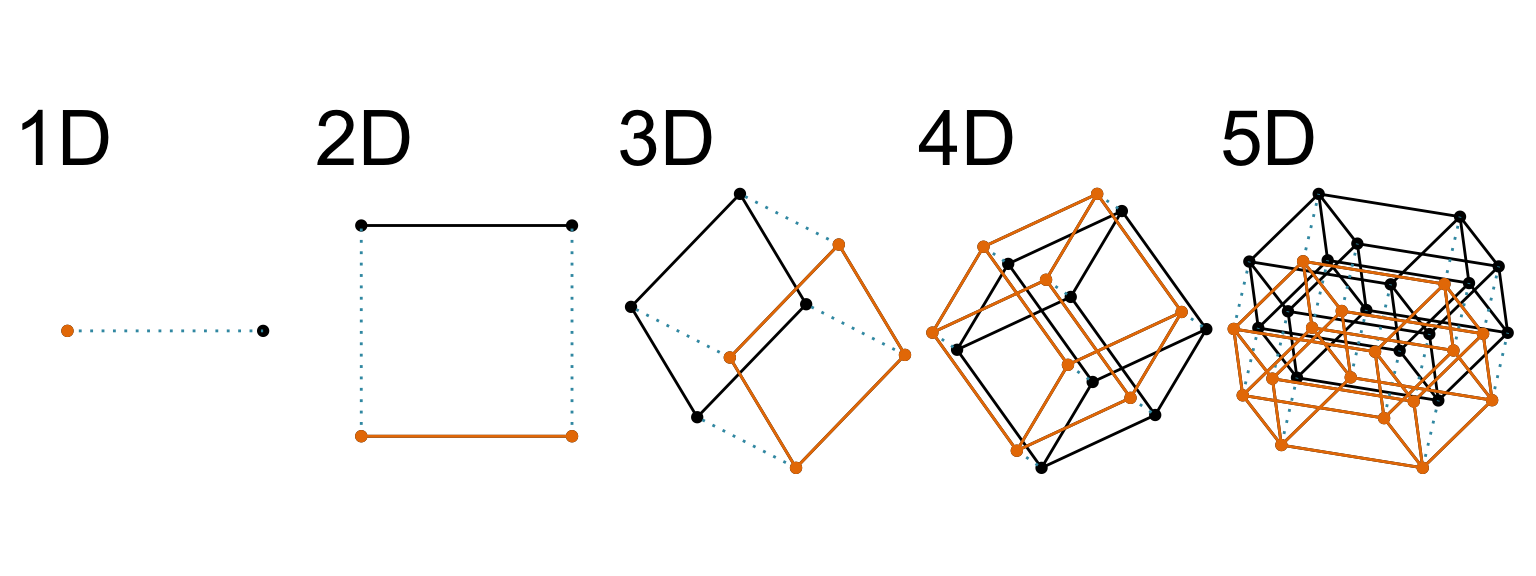
Increasing dimension adds an additional orthogonal axis.

If you want more high-dimensional shapes there is an R package, geozoo, which will generate cubes, spheres, simplices, mobius strips, torii, boy surface, klein bottles, cones, various polytopes, …

And read or watch Flatland: A Romance of Many Dimensions (1884) Edwin Abbott.

Notation: Data

\[\begin{eqnarray*} X_{~n\times p} = [X_{~1}~X_{~2}~\dots~X_{~p}]_{~n\times p} = \left[ \begin{array}{cccc} x_{~11} & x_{~12} & \dots & x_{~1p} \\ x_{~21} & x_{~22} & \dots & x_{~2p}\\ \vdots & \vdots & & \vdots \\ x_{~n1} & x_{~n2} & \dots & x_{~np} \end{array} \right]_{~n\times p} \end{eqnarray*}\]

Notation: Projection

\[\begin{eqnarray*} A_{~p\times d} = \left[ \begin{array}{cccc} a_{~11} & a_{~12} & \dots & a_{~1d} \\ a_{~21} & a_{~22} & \dots & a_{~2d}\\ \vdots & \vdots & & \vdots \\ a_{~p1} & a_{~p2} & \dots & a_{~pd} \end{array} \right]_{~p\times d} \end{eqnarray*}\]

Notation: Projected data

\[\begin{eqnarray*} Y_{~n\times d} = XA = \left[ \begin{array}{cccc} y_{~11} & y_{~12} & \dots & y_{~1d} \\ y_{~21} & y_{~22} & \dots & y_{~2d}\\ \vdots & \vdots & & \vdots \\ y_{~n1} & y_{~n2} & \dots & y_{~nd} \end{array} \right]_{~n\times d} \end{eqnarray*}\]

Why? (1/2)

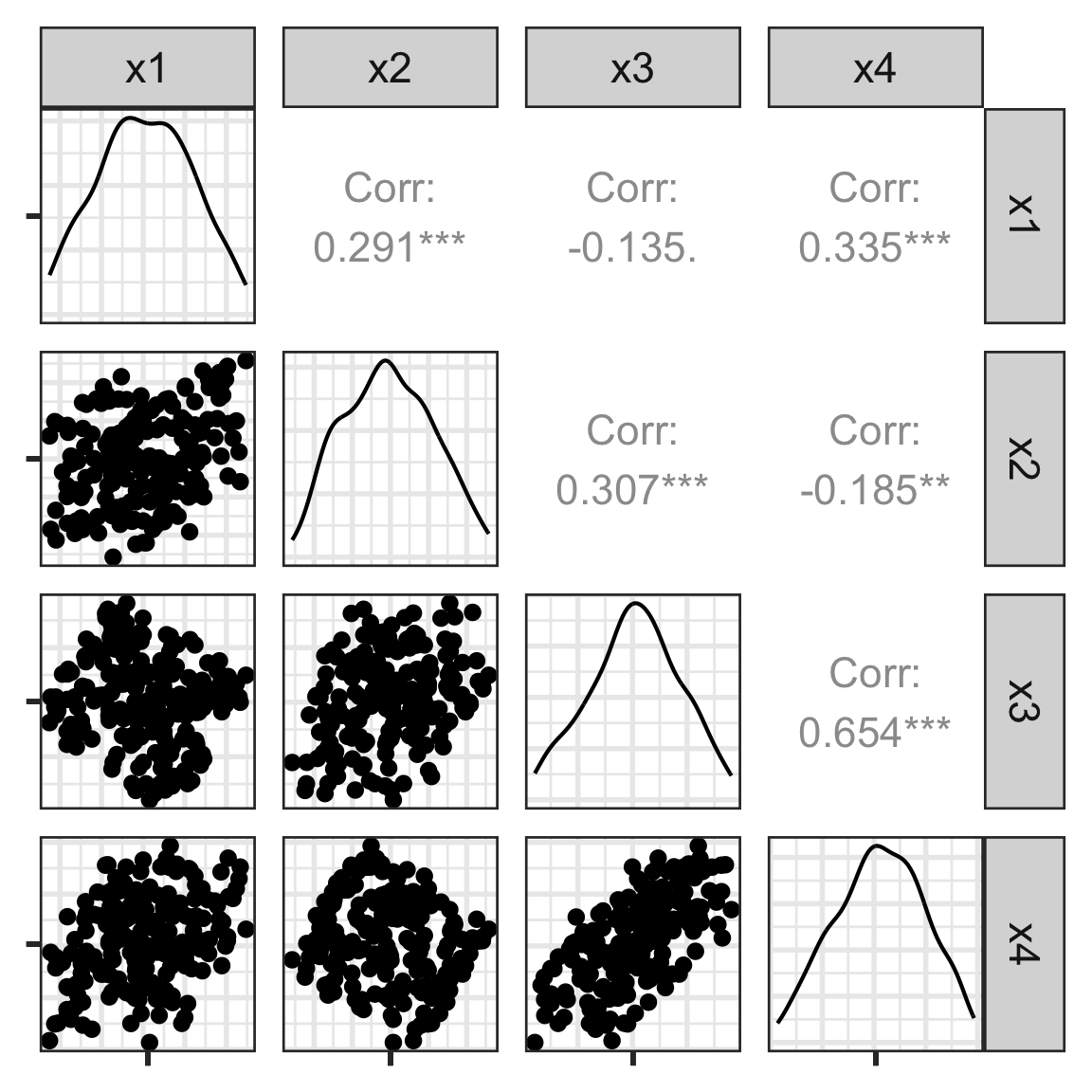
Scatterplot matrix

Here, we see linear association, clumping and clustering, potentially some outliers.

Why? (2/2)

There is an outlier in the data on the right, like the one in the left, but it is hidden in a combination of variables. It’s not visible in any pair of variables.

And help to see the data as a whole

To avoid misinterpretation …

… see the bigger picture!

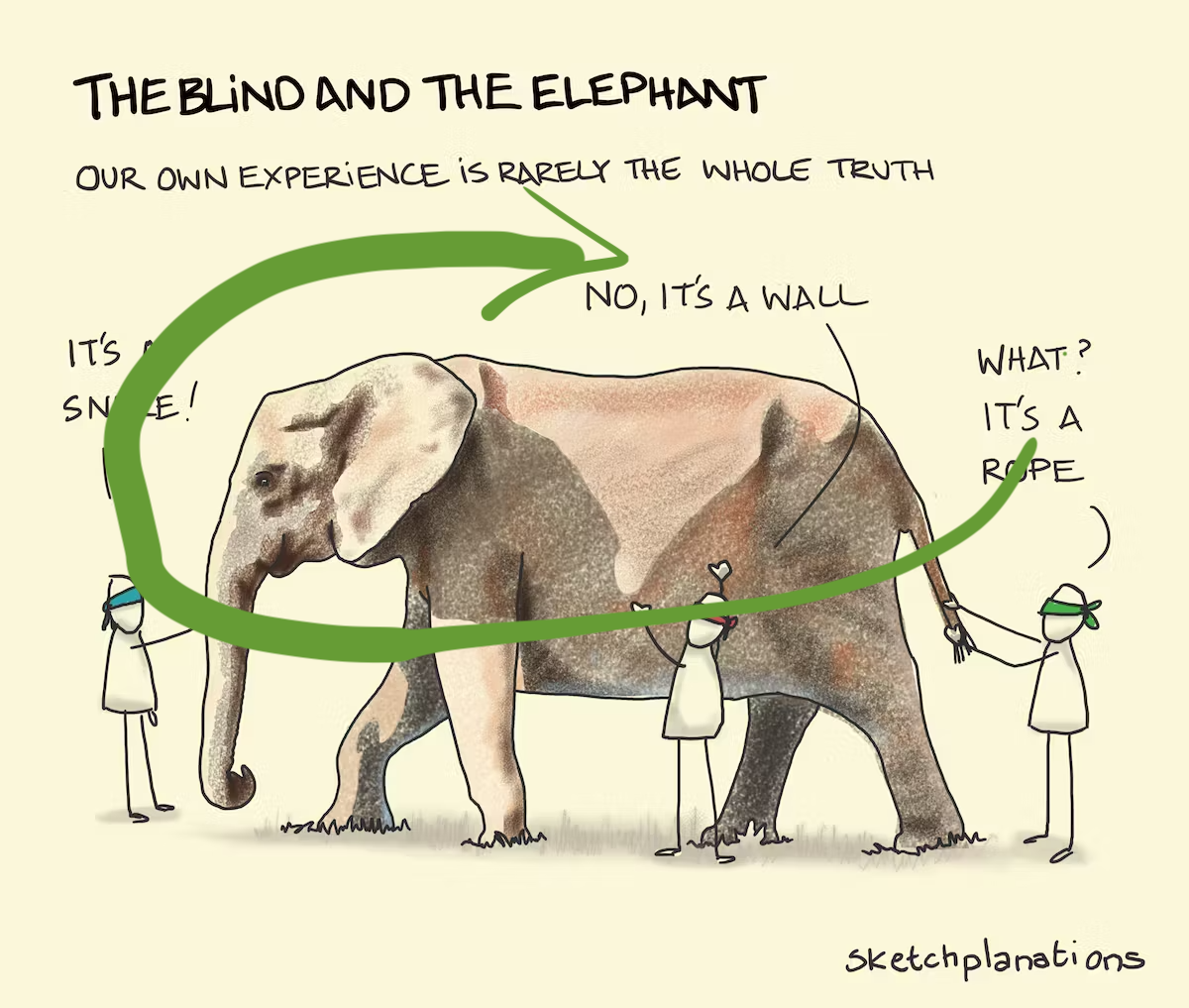
Image: Sketchplanations.

Tours of linear projections

Data is 2D: \(~~p=2\)

Projection is 1D: \(~~d=1\)

\[\begin{eqnarray*} A_{~2\times 1} = \left[ \begin{array}{c} a_{~11} \\ a_{~21}\\ \end{array} \right]_{~2\times 1} \end{eqnarray*}\]

Notice that the values of \(A\) change between (-1, 1). All possible values being shown during the tour.

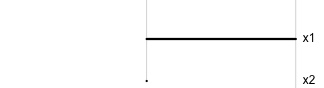
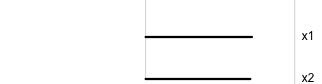
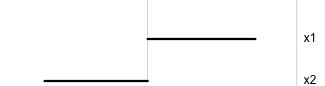
\[\begin{eqnarray*} A = \left[ \begin{array}{c} 1 \\ 0\\ \end{array} \right] ~~~~~~~~~~~~~~~~ A = \left[ \begin{array}{c} 0.7 \\ 0.7\\ \end{array} \right] ~~~~~~~~~~~~~~~~ A = \left[ \begin{array}{c} 0.7 \\ -0.7\\ \end{array} \right] \end{eqnarray*}\]

watching the 1D shadows we can see:

• unimodality
• bimodality, there are two clusters.

What does the 2D data look like? Can you sketch it?

Tours of linear projections

⟵
The 2D data

Tours of linear projections

Data is 3D: \(p=3\)

Projection is 2D: \(d=2\)

\[\begin{eqnarray*} A_{~3\times 2} = \left[ \begin{array}{cc} a_{~11} & a_{~12} \\ a_{~21} & a_{~22}\\ a_{~31} & a_{~32}\\ \end{array} \right]_{~3\times 2} \end{eqnarray*}\]

Notice that the values of \(A\) change between (-1, 1). All possible values being shown during the tour.

See:

• circular shapes
• some transparency, reveals middle
• hole in in some projections
• no clustering

Tours of linear projections

Data is 4D: \(p=4\)

Projection is 2D: \(d=2\)

\[\begin{eqnarray*} A_{~4\times 2} = \left[ \begin{array}{cc} a_{~11} & a_{~12} \\ a_{~21} & a_{~22}\\ a_{~31} & a_{~32}\\ a_{~41} & a_{~42}\\ \end{array} \right]_{~4\times 2} \end{eqnarray*}\]

How many clusters do you see?

• three, right?
• one separated, and two very close,
• and they each have an elliptical shape.

• do you also see an outlier or two?

Intuitively, tours are like …

Anomaly is no longer hidden

Wait for it!

How to use a tour in R

This is a basic tour, which will run in your RStudio plot window.

library(tourr)
animate_xy(flea[, 1:6], rescale=TRUE)

This data has a class variable, species.

flea |> slice_head(n=3)

   species tars1 tars2 head aede1 aede2 aede3
1 Concinna   191   131   53   150    15   104
2 Concinna   185   134   50   147    13   105
3 Concinna   200   137   52   144    14   102

Use this to colour points with:

animate_xy(flea[, 1:6], 
           col = flea$species, 
           rescale=TRUE)

You can specifically guide the tour choice of projections using

animate_xy(flea[, 1:6], 
           tour_path = guided_tour(holes()), 
           col = flea$species, 
           rescale = TRUE, 
           sphere = TRUE)

and you can manually choose a variable to control with:

set.seed(915)
animate_xy(flea[, 1:6], 
           radial_tour(basis_random(6, 2), 
                       mvar = 6), 
           rescale = TRUE,
           col = flea$species)

How to save a tour

To save as an animated gif:

set.seed(645)
render_gif(penguins_sub[,1:4],
           grand_tour(),
           display_xy(col="#EC5C00",
             half_range=3.8, 
             axes="bottomleft", cex=2.5),
           gif_file = "gifs/penguins1.gif",
           apf = 1/60,
           frames = 1500,
           width = 500, 
           height = 400)

Your turn

Use a grand tour on the data set c1 in the mulgar package. What shapes do you see?

library(tourr)
library(mulgar)
animate_xy(c1)

Have a look at c3 or c7 also. How are the structures different.

05:00

Dimension reduction

What is dimensionality?

When an axis extends out of a direction where the points are collapsed, it means that this variable is partially responsible for the reduced dimension.

In high-dimensions

2D plane in 5D

3D plane in 5D

5D plane in 5D

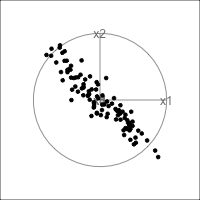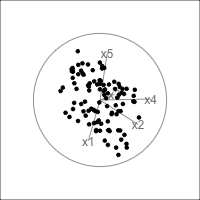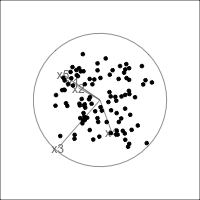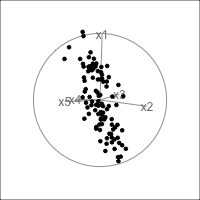
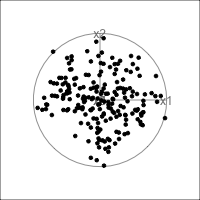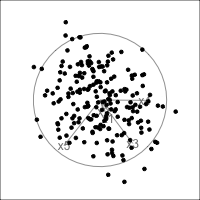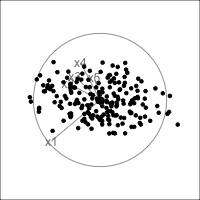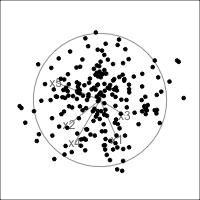
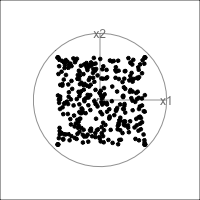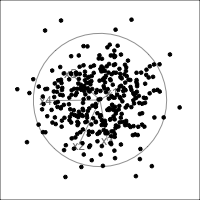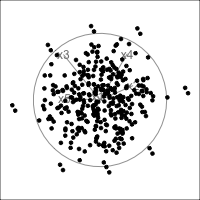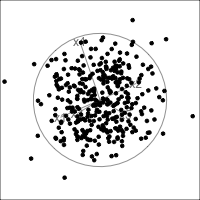
Principal component analysis (PCA) will detect these dimensionalities.

Some data is basically univariate

Mostly skewed variables, some outliers, without much association.

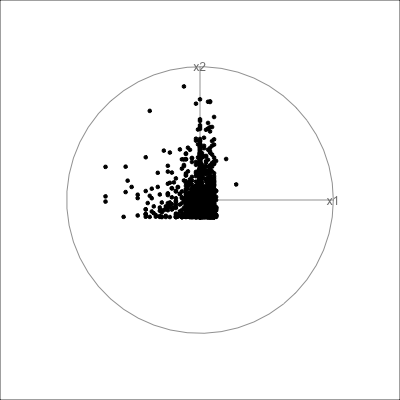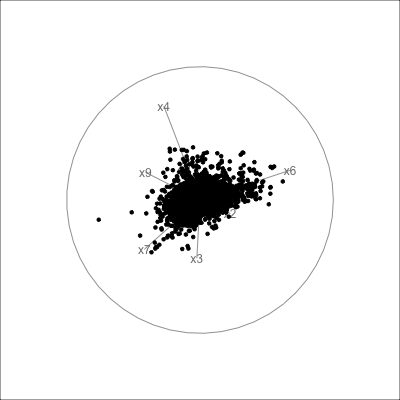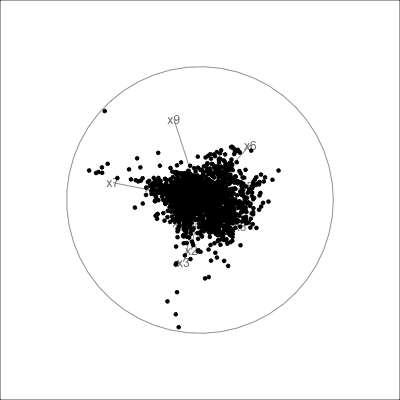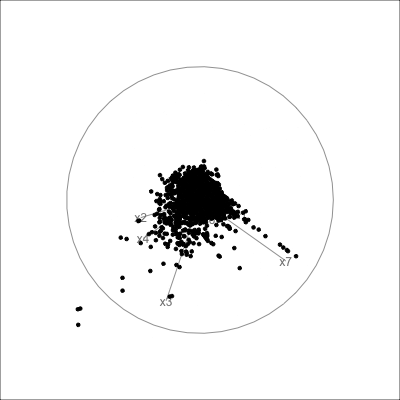
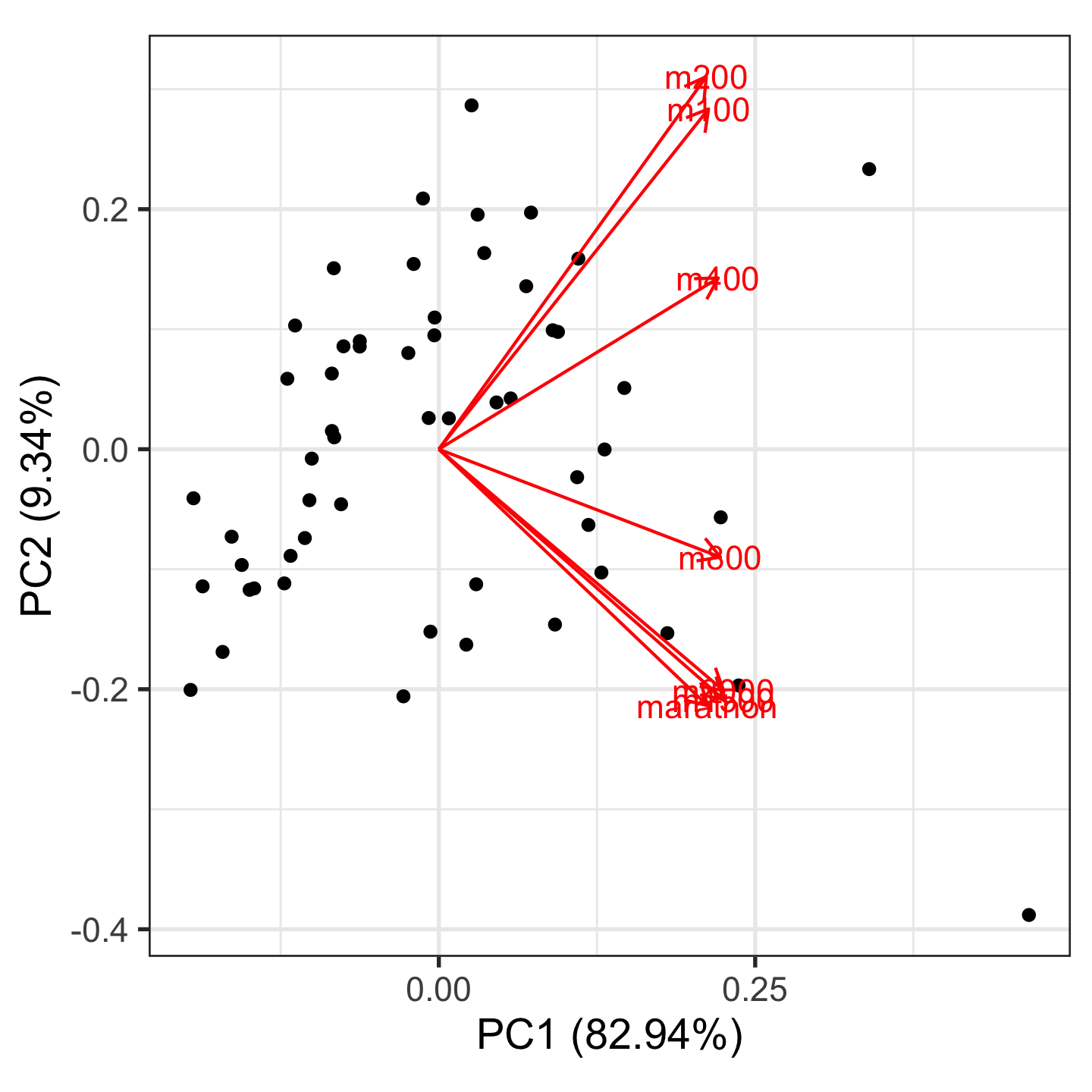
Example: womens’ track records (1/3)

Source: Johnson and Wichern, Applied multivariate analysis

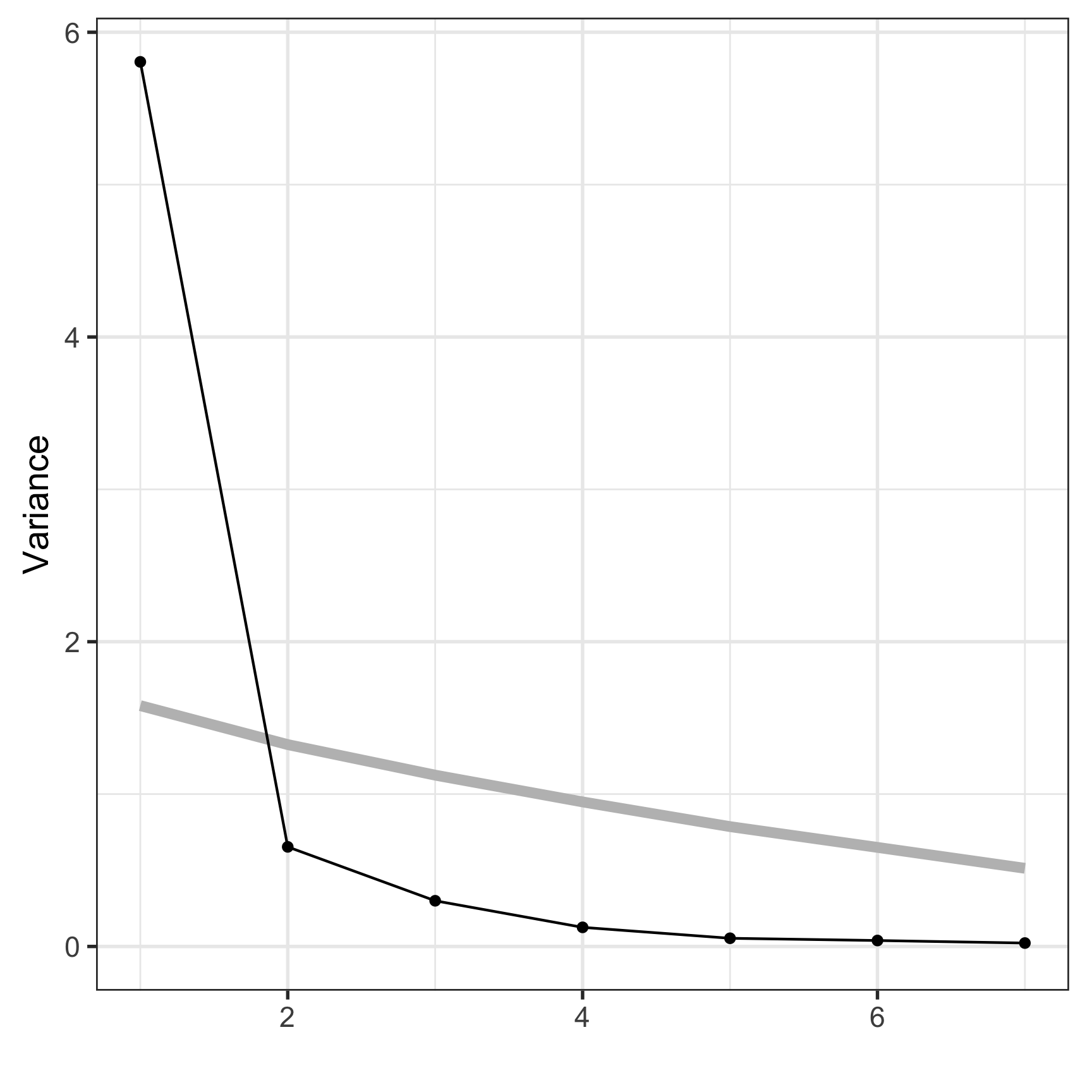
Example: PCA summary (2/3)

Variances/eigenvalues

[1] 5.806 0.654 0.300 0.125 0.054 0.039 0.022

Component coefficients

          PC1   PC2    PC3    PC4
m100     0.37  0.49 -0.286  0.319
m200     0.37  0.54 -0.230 -0.083
m400     0.38  0.25  0.515 -0.347
m800     0.38 -0.16  0.585 -0.042
m1500    0.39 -0.36  0.013  0.430
m3000    0.39 -0.35 -0.153  0.363
marathon 0.37 -0.37 -0.484 -0.672

How many PCs?

Example: Visualise (3/3)

Biplot: data in the model space

2D model in data space

track_model <- mulgar::pca_model(track_std_pca, d=2, s=2)
track_all <- rbind(track_model$points, track_std[,1:7])
animate_xy(track_all, edges=track_model$edges,
           edges.col="#E7950F", 
           edges.width=3, 
           axes="off")

Key conceptual points

• Avoid misinterpretation, by using your high-dimensional visualisation skills to look at the data as a whole.
• Examine model fit by by examining the model overlaid on the data, model-in-the-data-space. (Wickham et al (2015) Removing the Blindfold)

End of session 1

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.