Creating data plots for effective decision-making using statistical inference with R

Dianne Cook
Monash University

Session 1: Making effective plots using ggplot2’s grammar of graphics

Outline

time topic
1:40-1:55 Why, philosophy and benefits
1:55-2:15 Organising data to map variables to plots
2:15-2:45 Making a variety of plots
2:45-3:10 Do but don’t, and cognitive principles
3:10-3:40 COFFEE BREAK

Why

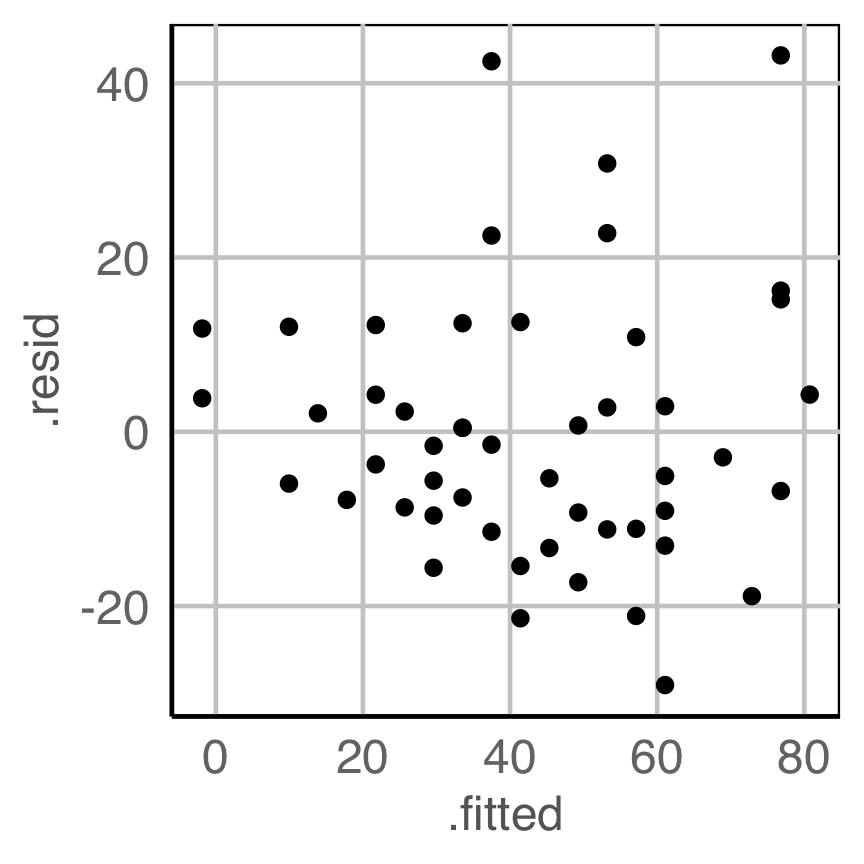
Is there any pattern in the residuals that indicate a problem with the model fit?

Why



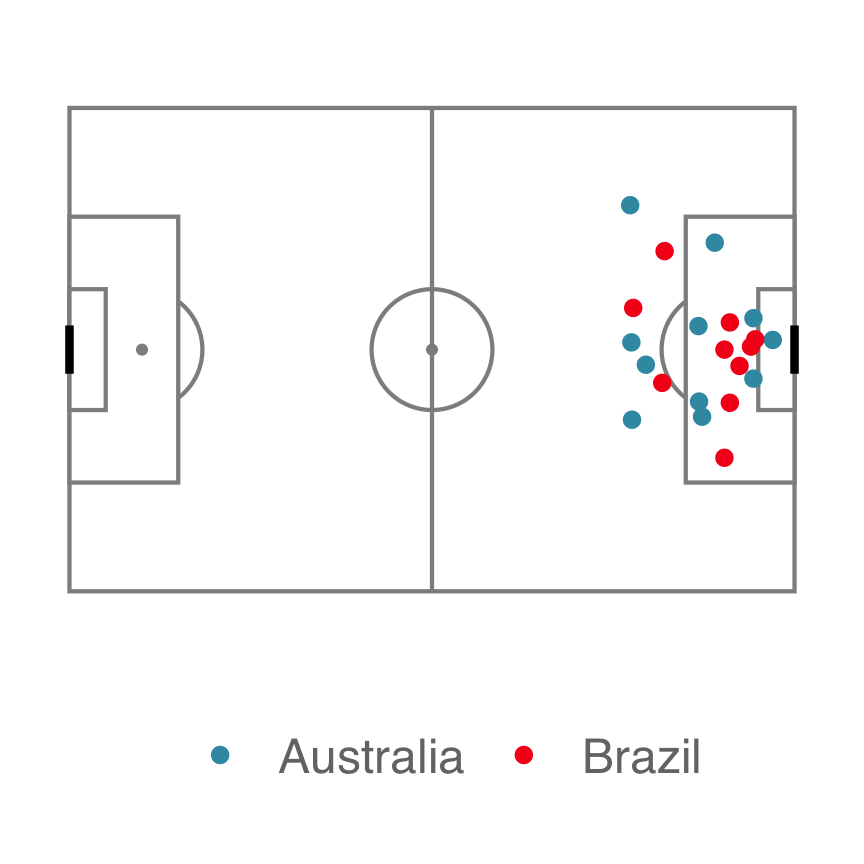
Do the teams have different shot styles?

(From the Women’s 2019 World Cup Soccer)

Why


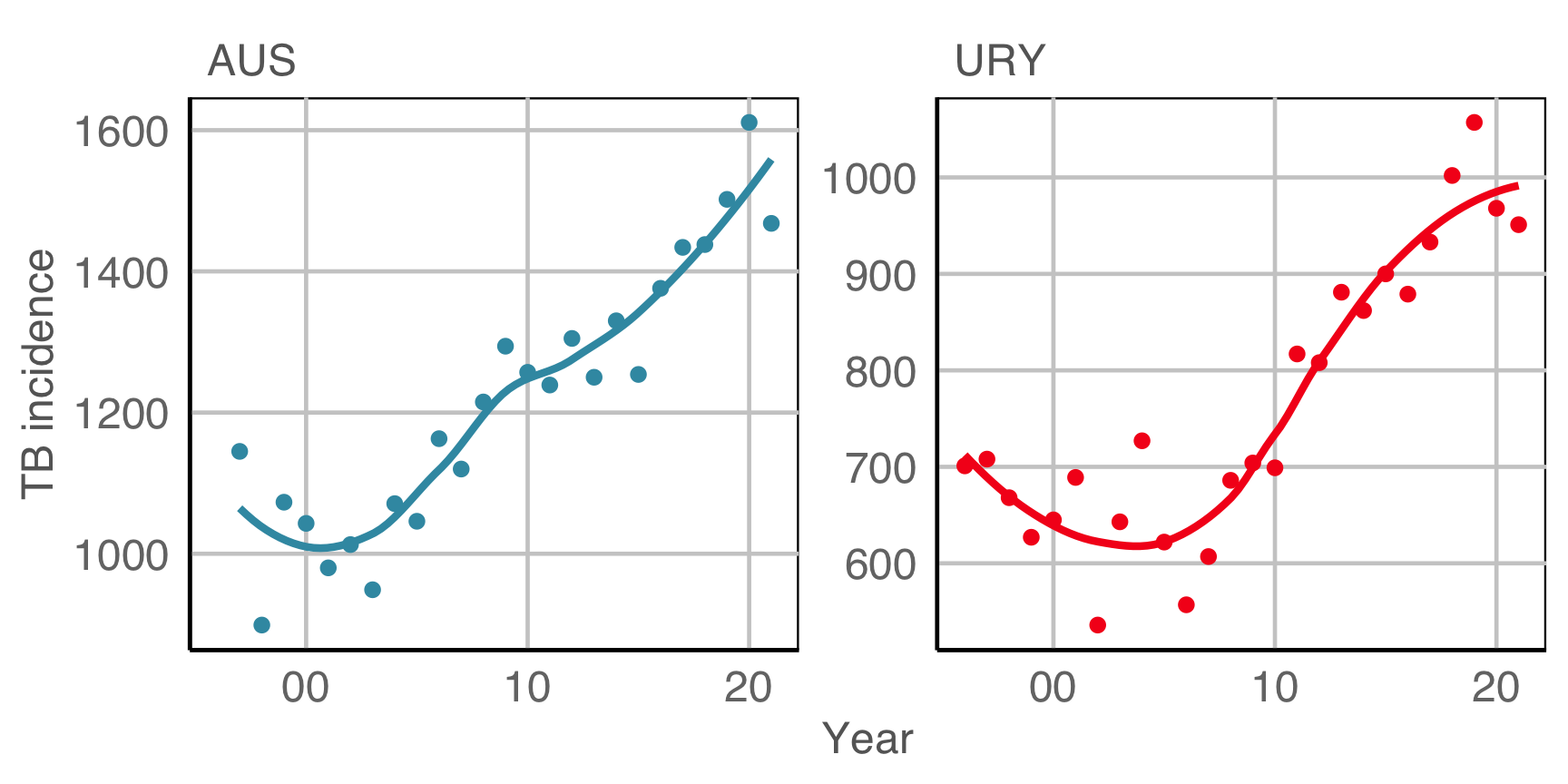
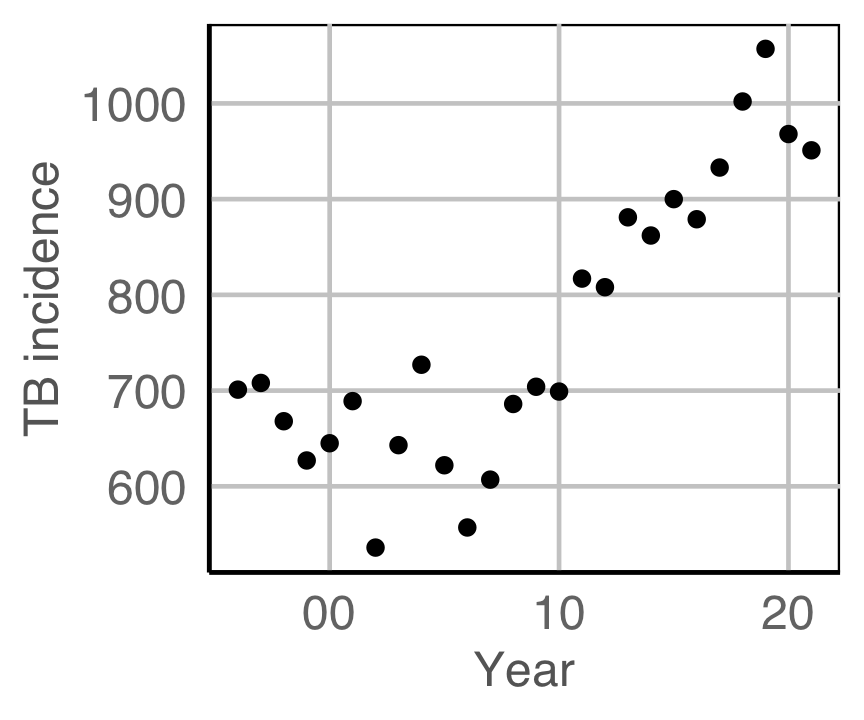
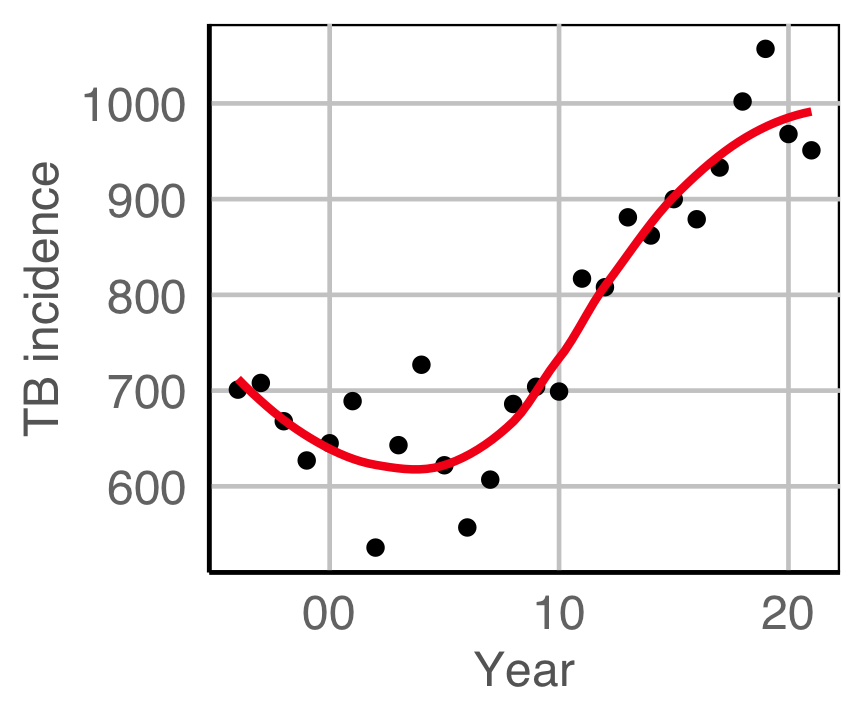
Is TB getting worse? (In Australia and Uruguay)

(From the World Health Organisation (WHO)]

Why


Which is the best display to answer the previous question?

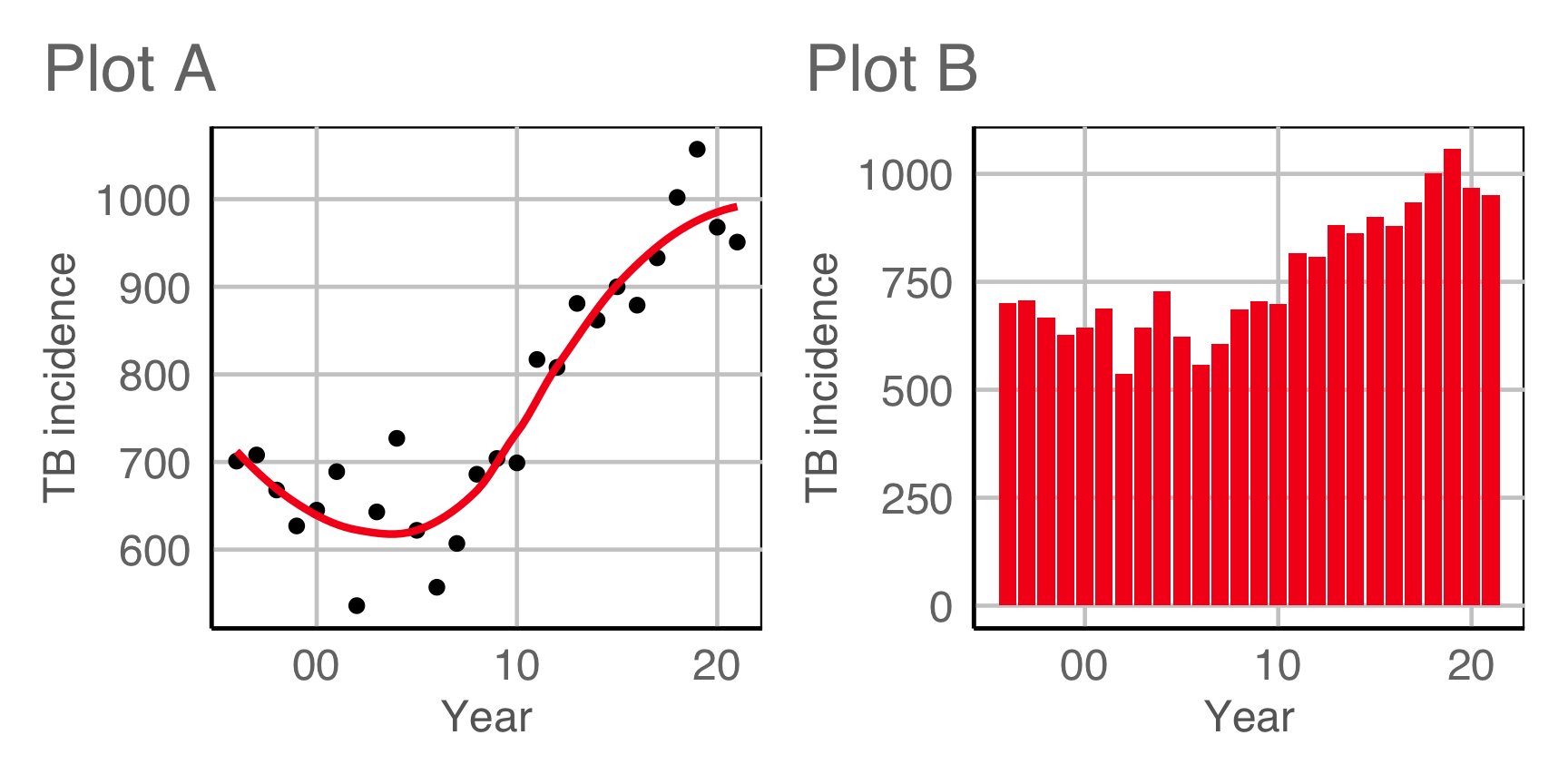
What’s the goal?


Reading data plots is subjective.


Making decisions based on data visualisations is common, where we need to be objective .




It is possible, and here is how we do that …

These are the tools you need

install.packages("ggplot2")

or better yet:

install.packages("tidyverse")
  • Define your plots using a grammar that maps variables in tidy data to elements of the plot.
  • Wrangle your data into tidy form for clarity of plot specification.

space 

install.packages("nullabor")
  • Compare your data plot to plots of null data.
  • This checks whether what we see is real or spurious.
  • Also allows for measuring the effectiveness of one plot design vs another.

Organising your data to enable mapping variables to graphical elements

Tidy data





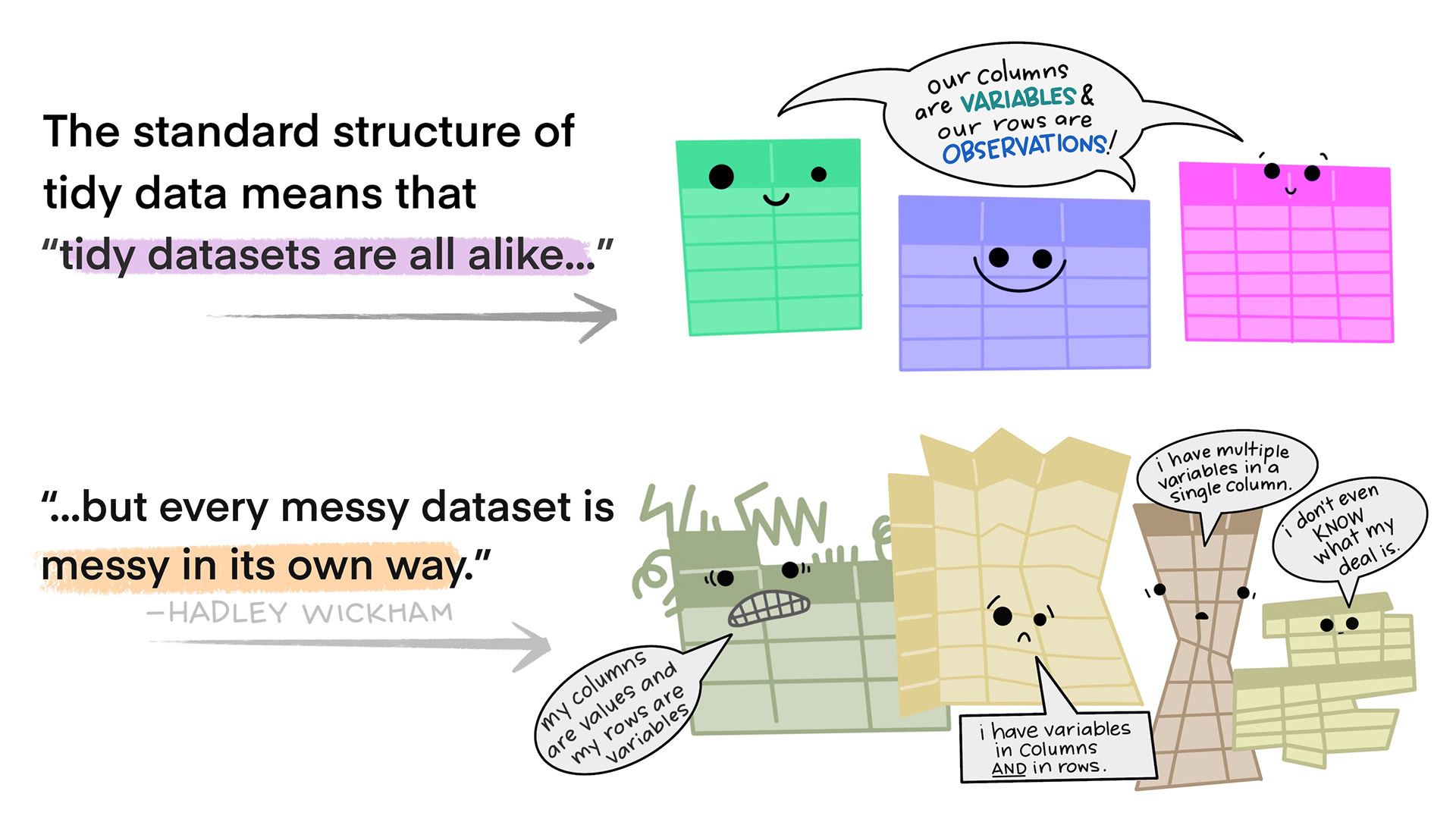
  1. Each variable forms a column
  2. Each observation forms a row
  3. Each type of observational unit forms a table. If you have data on multiple levels (e.g. data about houses and data about the rooms within those houses), these should be in separate tables.

Illustrations from the Openscapes blog Tidy Data for reproducibility, efficiency, and collaboration by Julia Lowndes and Allison Horst

YOUR TURN

For each of the following data discuss whether it is in tidy form.

Data 1: tuberculosis from WHO

Data 2: Graduate programs

Data 3: GHCN weather station records

Answers

Data 1:
Not in tidy form

  • iso3
  • year
  • gender
  • age

Data 2:
It’s in tidy form!

  • subject
  • inst
  • AvNumPubs
  • AvNumCits
  • …

Data 3:
Not in tidy form

  • station
  • year
  • month
  • day
  • TMAX
  • TMIN
  • PRCP

Statistical data

\[X = \left[ \begin{array}{rrrr} X_{~1} & X_{~2} & ... & X_{~p} \end{array} \right] \\ = \left[ \begin{array}{rrrr} X_{~11} & X_{~12} & ... & X_{~1p} \\ X_{~21} & X_{~22} & ... & X_{~2p} \\ \vdots & \vdots & \ddots& \vdots \\ X_{~n1} & X_{~n2} & ... & X_{~np} \end{array} \right]\]

  • This is tidy data!
  • You might also make assumptions about the distribution of each variable, e.g. \(X_{~1} \sim N(0,1), ~~X_{~2} \sim \text{Exp}(1) ...\)

Mapping

In ggplot2, the variables from tidy data are explicitly mapped to elements of the plot, using aesthetics.

Basic Mappings

  • x and y to plot points in a two-dimensional space
  • color, fill to render as a color scale
  • size maps variable to size of object
  • shape maps variable to different shapes

Depending on the geom different mappings are possible, xmin, xend, linetype, alpha, stroke, weight …

Facets

Variables are used to subset (or condition)

Layers

Different data can be mapped onto the same plot, eg observations, and means

Example

ggplot(mpg, 
       aes(
         x=displ, 
         y=hwy, 
         color=class)) + 
  geom_point()

displ is mapped to x
hwy is mapped to y
class is mapped to color.

Common plot descriptions as scripts

Example 1A

How are variables mapped to create this plot?



Code for URY TB plot 
ggplot(tb_ury, 
       aes(x=year, 
           y=c_newinc)) + 
  geom_point() +
  scale_x_continuous("Year", 
    breaks = seq(1980, 2020, 10), 
    labels = c("80", "90", "00", "10", "20")) +
  ylab("TB incidence")

Example 1B

How are variables mapped to create this plot?



Code for URY TB plot 
ggplot(tb_ury, aes(x=year, y=c_newinc)) + 
  geom_point() +
  geom_smooth(se=F, colour="#F5191C") +
  scale_x_continuous("Year", breaks = seq(1980, 2020, 10), labels = c("80", "90", "00", "10", "20")) +
  ylab("TB incidence")

Example 2A

How are variables mapped to create this plot?



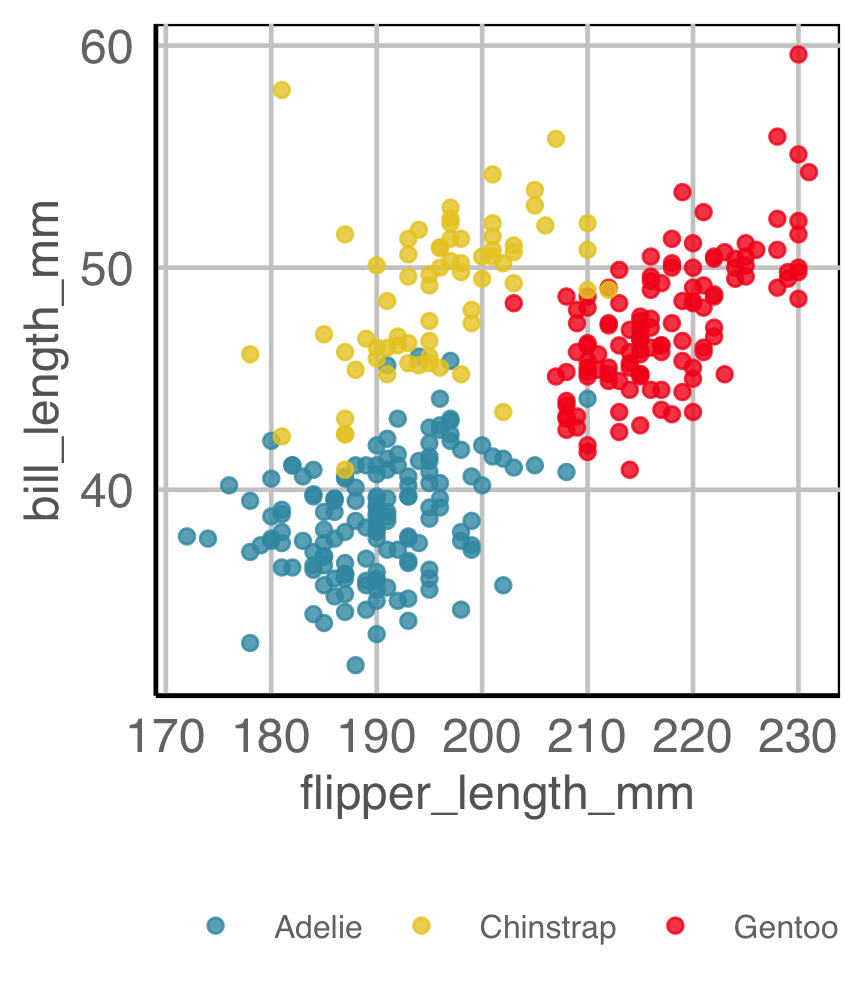
Code for penguins plot 
ggplot(penguins, 
       aes(x=flipper_length_mm, 
           y=bill_length_mm, 
           color=species)) + 
  geom_point(alpha=0.8) +
  scale_color_discrete_divergingx(palette="Zissou 1") +
  theme(legend.title = element_blank(), 
        legend.position = "bottom",
        legend.direction = "horizontal",
        legend.text = element_text(size="8"))

Example 2B

How are variables mapped to create this plot?



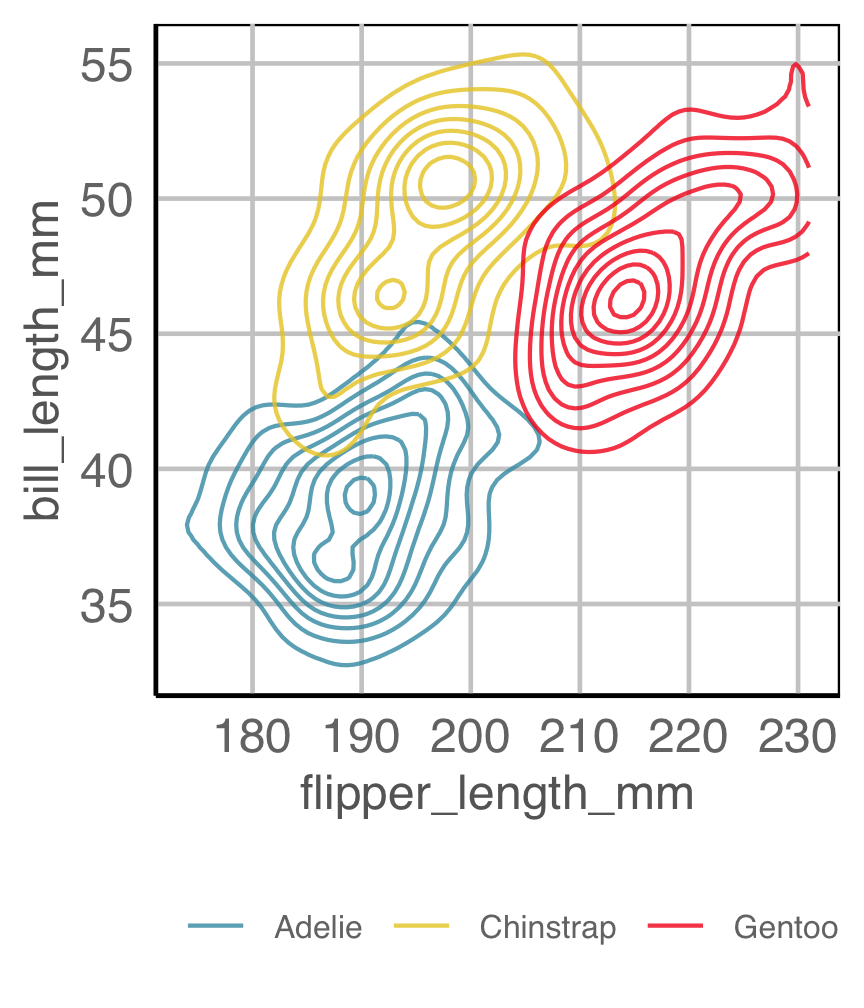
Code for penguins plot 
ggplot(penguins, 
       aes(x=flipper_length_mm, 
           y=bill_length_mm, 
           color=species)) + 
  geom_density2d(alpha=0.8) +
  scale_color_discrete_divergingx(palette="Zissou 1") +
  theme(legend.title = element_blank(), 
        legend.position = "bottom",
        legend.direction = "horizontal",
        legend.text = element_text(size="8"))

Example 3 (1/5)

First get the data in tidy form

tb_ury_sa <- tb_ury %>%
  filter(year > 2012) %>%
  select(iso3, year, 
         newrel_f014:newrel_f65, 
         newrel_m014:newrel_m65) %>%
  pivot_longer(cols=newrel_f014:newrel_m65,
               names_to = "sex_age", 
               values_to = "count") %>%
  filter(!is.na(count)) %>%
  separate(sex_age, into=c("stuff", 
                           "sex_age")) %>%
  mutate(sex = str_sub(sex_age, 1, 1),
         age = str_sub(sex_age, 2, 
                       str_length(sex_age))) %>%
  mutate(age = case_when(
    age == "014" ~ "0-14",
    age == "1524" ~ "15-24",
    age == "2534" ~ "25-34",
    age == "3544" ~ "35-44",
    age == "4554" ~ "45-54",
    age == "5564" ~ "55-64",
    age == "65" ~ "65")) %>%
  select(iso3, year, sex, age, count)


Example 3 (2/5)

How many ways can we plot all three variables?


geom: bar + position (stack, dodge, fill)

aes:

  • Var 1 to x
  • count to y
  • Var 2 to color
  • Var 3 to facet

geom: point + smooth

aes:

  • Var 1 to x
  • count to y
  • Var 2 to color
  • Var 3 to facet

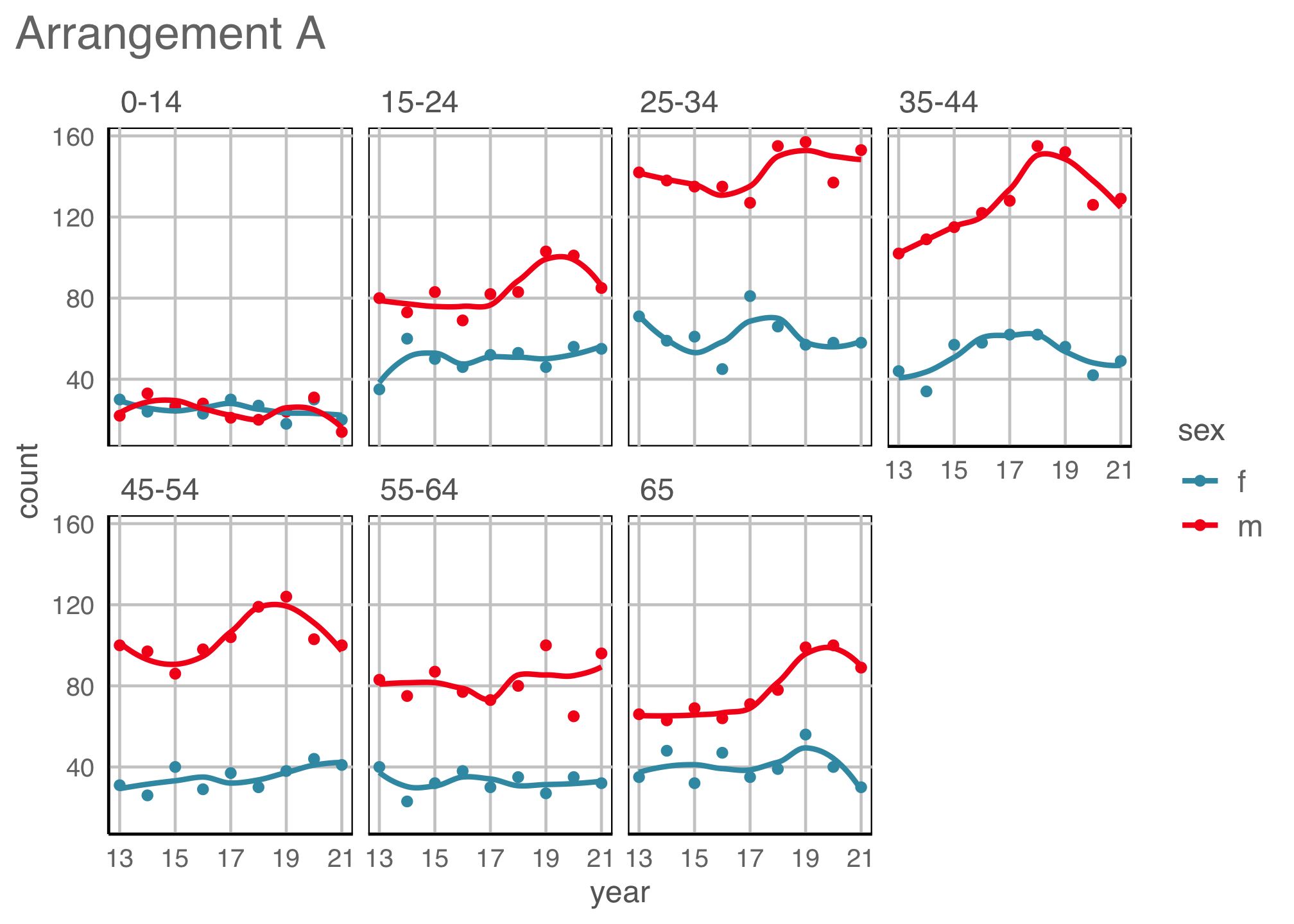
Example 3 (3/5)

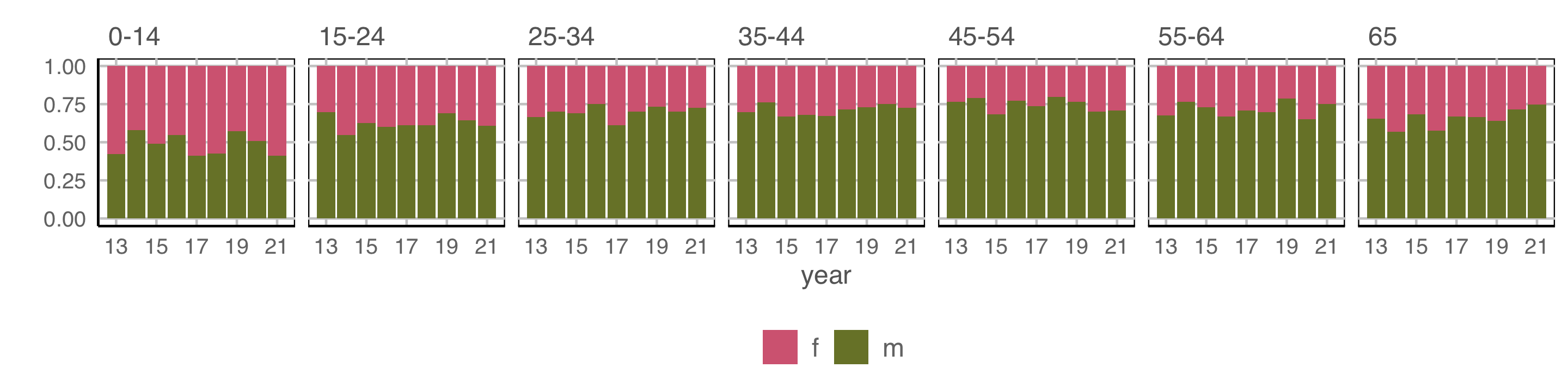
How are variables mapped to create this plot?

geom: bar/position=“fill”

year to x \(~~~~\) count to y \(~~~~\) fill to sex \(~~~~\) facet by age


Observations: More incidence among males, especially with age. No clear temporal trend.

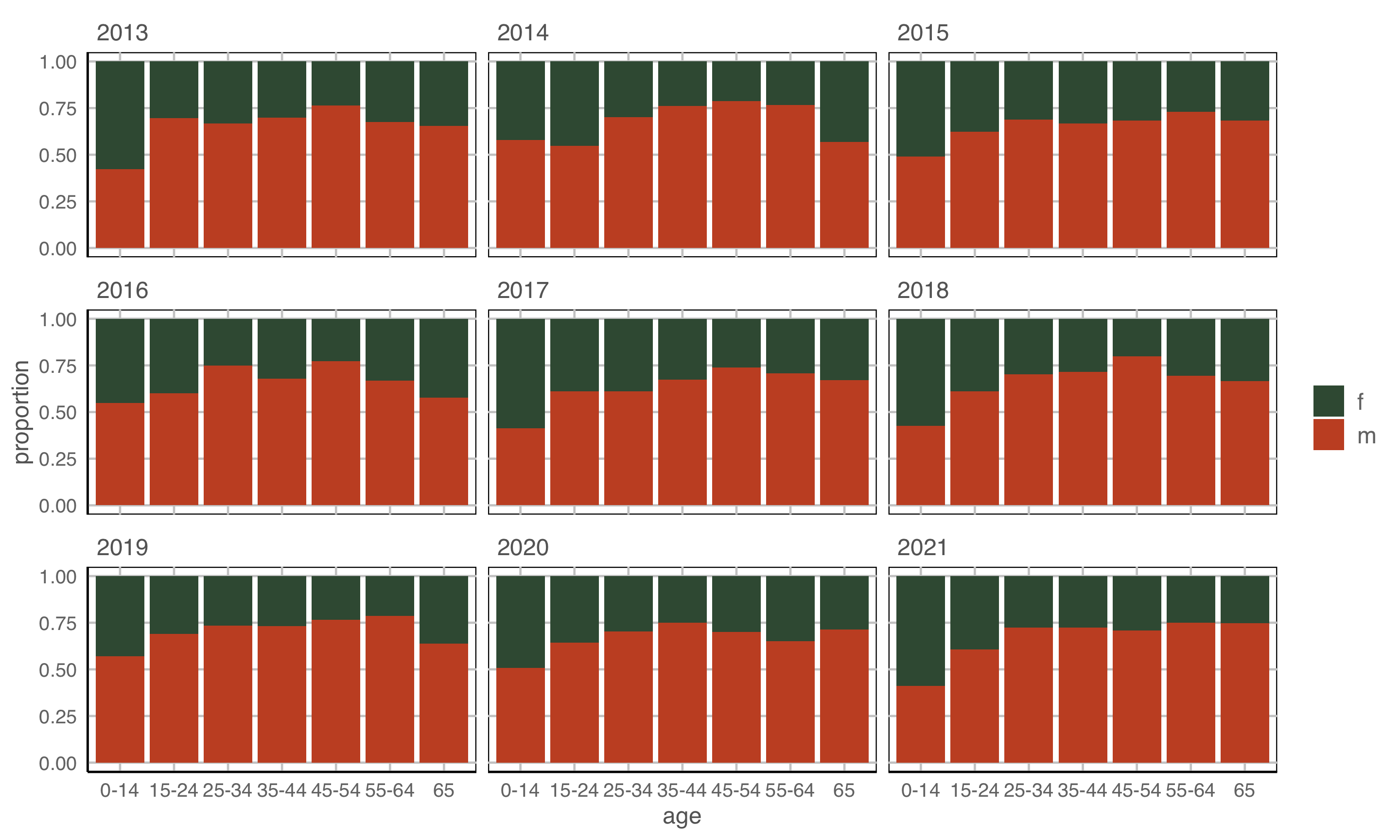
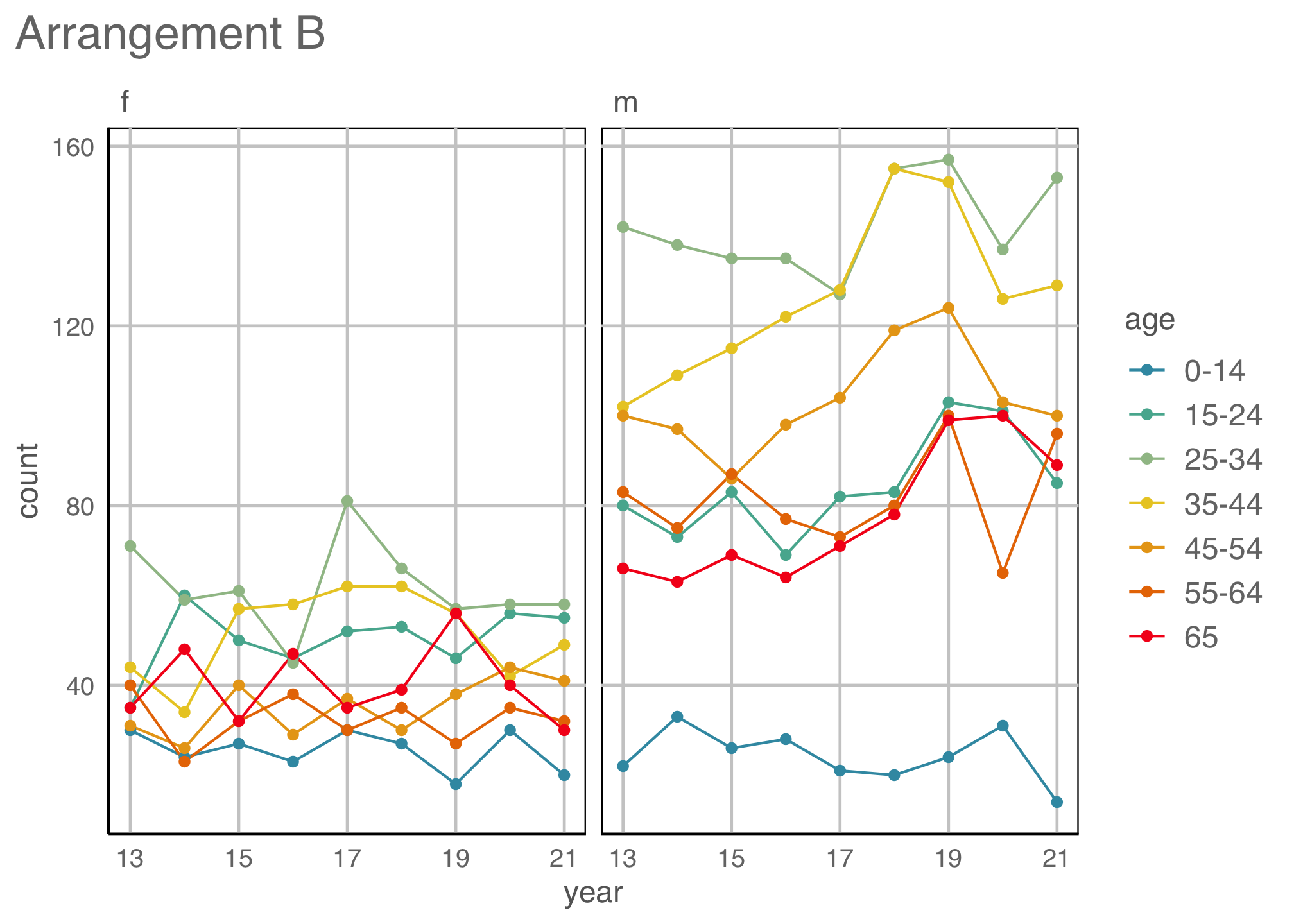
Example 3 (4/5)

geom: bar

year to x \(~\) count to y \(~\) fill and facet to sex \(~\) facet by age

Incidence is higher in the middle age groups.

Where’s the temporal trend?

Example 3 (5/5)

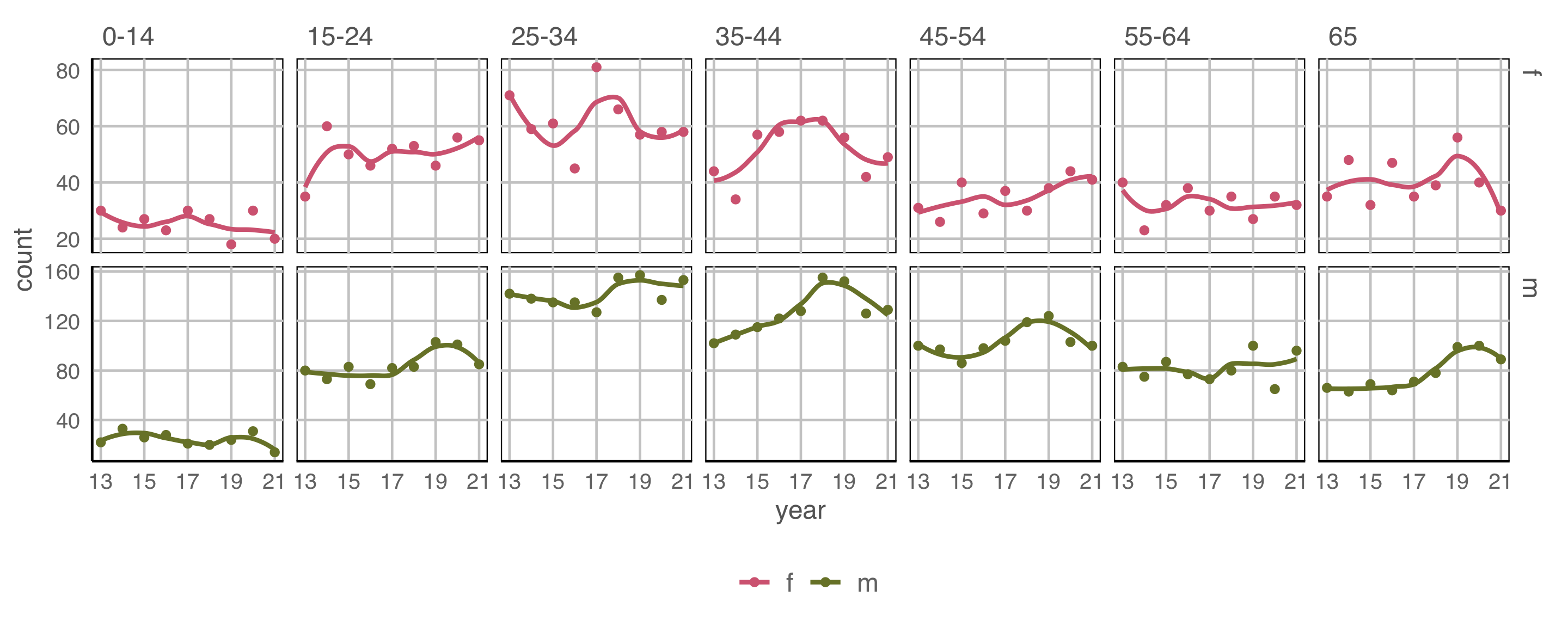
geom: point, smooth

year to x \(~\) count to y \(~\) colour and facet to sex \(~\) facet by age


Temporal trend is mostly with males.

Tidy data to many plot descriptions

ggplot(tb_ury_sa, 
       aes(x=year, 
           y=count, 
           fill=sex)) + 
  geom_col(position="fill") +
  facet_wrap(~age)
ggplot(tb_ury_sa, 
       aes(x=year, 
           y=count, 
           fill=sex)) + 
  geom_col() +
  facet_grid(sex~age)
ggplot(tb_ury_sa, 
       aes(x=year, 
           y=count, 
           colour=sex)) + 
  geom_point() +
  geom_smooth() +
  facet_grid(sex~age)

?

ggplot(tb_ury_sa, 
       aes(x=age, 
           y=count, 
           fill=sex)) + 
  geom_col(position="fill") +
  facet_wrap(~year)

Re-arrangements

Scaling

This might have slipped under the radar, but different displays had some different scaling of the data:

Slides 6, 27, 28 (Why, Example 3 4,5/5) were constructed with

facet_wrap(..., scales="free_y")


Why?

The emphasis was comparing difference in trend not magnitude of values.

YOUR TURN

  1. Create two new plot arrangements of the Uruguay TB data. What do they put the focus on?
  2. Change the scaling on one of the plots, where it will change it. How does the information change?

Do’s and don’ts

Plot descriptions

Use a new variable in a single data set - avoid multiple data sets (Tidy data principle)

GOOD

ggplot(tb_sub, aes(x=year, 
                   y=c_newinc, 
                   colour=iso3)) + 
  geom_point() +
  geom_smooth(se=F) +
  facet_wrap(~iso3, ncol=2, 
             scales="free_y") +
  theme(legend.position = "none")

BAD

ggplot() + 
  geom_point(data = tb_ury, 
    aes(x=year, y=c_newinc), 
    colour="#F5191C") +
  geom_point(data = tb_aus, 
    aes(x=year, y=c_newinc), 
    colour="#3B99B1") +
  geom_smooth(data = tb_ury, 
    aes(x=year, y=c_newinc), 
    colour="#F5191C", se=F) +
  geom_smooth(data = tb_aus, 
    aes(x=year, y=c_newinc), 
    colour="#3B99B1", se=F)

Cognitive principles

Hierarchy of mappings

Cleveland and McGill (1984)



Illustrations made by Emi Tanaka

Hierarchy of mappings

  1. Position - common scale (BEST)
  2. Position - nonaligned scale
  3. Length, direction, angle
  4. Area
  5. Volume, curvature
  6. Shading, color (WORST)
  1. scatterplot, barchart
  2. side-by-side boxplot, stacked barchart
  3. piechart, rose plot, gauge plot, donut, wind direction map, starplot
  4. treemap, bubble chart, mosaicplot
  5. chernoff face
  6. choropleth map

Proximity

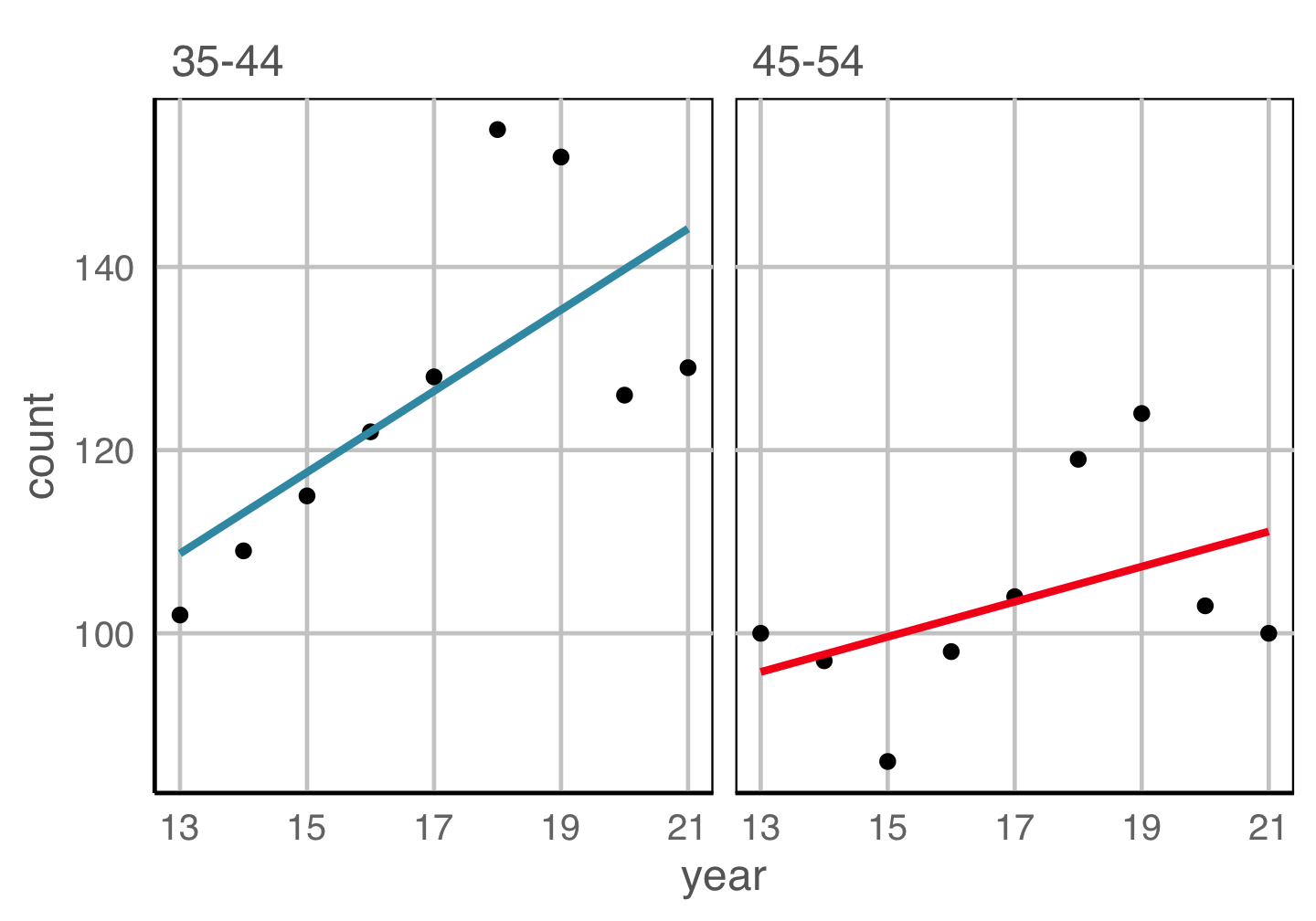
Place elements that you want to compare close to each other. If there are multiple comparisons to make, you need to decide which one is most important.

Change blindness

Making comparisons across plots requires the eye to jump from one focal point to another. It may result in not noticing differences.


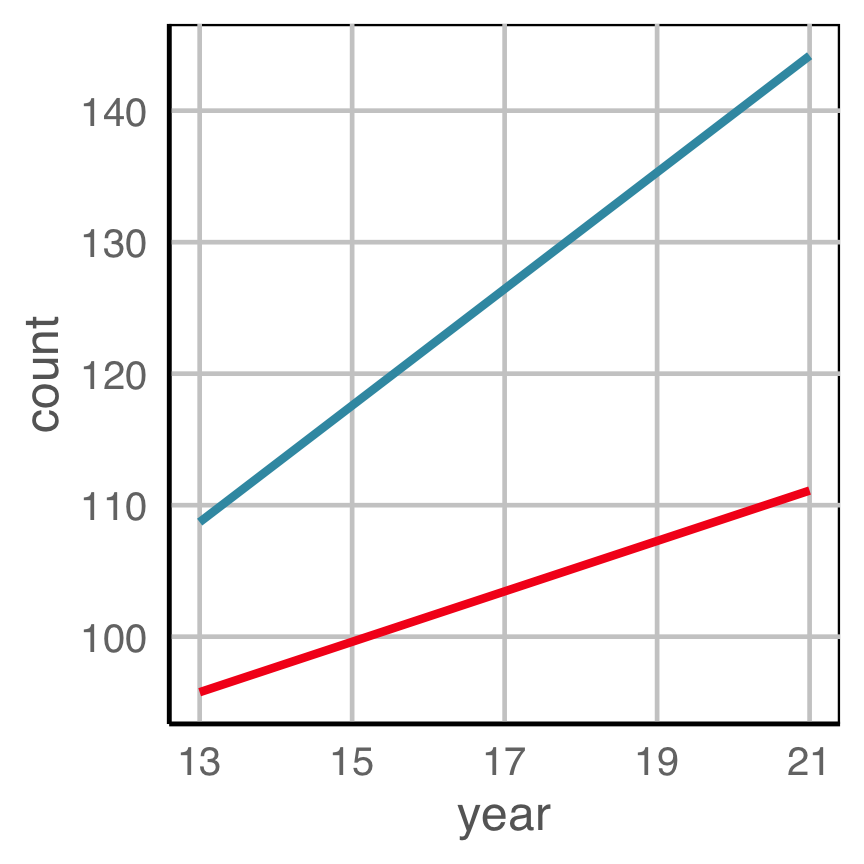
YOUR TURN

Take the following plot, and make it more difficult to read.

library(nullabor)
data(electoral)
ggplot(electoral$polls, 
       aes(x=Democrat, 
           y=Margin)) +
  geom_boxplot()

End of session 1

Creative Commons License
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

https://dicook.github.io/LatinR